Design of an Efficient Binary Vedic Multiplier for High Speed Applications Using Vedic Mathematics with Bit Reduction Technique ()
Received 2 April 2016; accepted 20 April 2016; published 27 July 2016

1. Introduction
Vedic Mathematics is the technique used in an Ancient India for solving arithmetical problems mentally and in easier way. It contains 16 formulas and 13 sub-formulas. These sutras are used in solving complex computations, and executing them manually. It is operated on 16 sutras and 13 up-sutras. The algorithms and principles of all sutras were given in [1] . Urdhva Tiryakbhyam Sutra is mainly used for multiplication which means “Vertically and Crosswise”. The multiplier based on this sutra is known as Vedic multiplier. It is based on a novel concept of array multiplication. In [2] , the design and implementation of Triyakbhyam were done and the speed was compared with Nikhilam sutra, squaring and cubing algorithm.
In [3] , the implementation of Arithmetic unit that used the Vedic mathematics algorithm for multiplication was discussed. The arithmetic unit was designed to perform multiplication, addition and subtraction and multiply accumulation operations. The MAC unit uses a fast multiplier built with Vedic Mathematics algorithm. The square, cube algorithms along with Karatsuba algorithm have been discussed in [3] , to reduce the multiplications required. In [4] , a ROM based multiplier is proposed. One out of two inputs is fixed here. So this method can be used in matrix multiplication and other applications which use constant coefficient multiplication. The faster Vedic multiplier consumes more power than convention ones. In [5] , the multiplier based on Nikhilam sutra was presented with modification in 2’s complement block and multiplication block. 7-bit encoding technique is employed in the design of multiple radix multipliers. The high speed 32 × 32 bit Vedic multiplier was presented in [6] . The binary implementation using carry save adder was presented in [6] and comparison result was made.
The iterative algorithm for Nikhilam sutra was presented in [7] . It reduces two larger numbers in to two smaller numbers by neglecting zeros from the least significant side and performing bit shifting to complete the multiplication operation. But this method demands for closeness of the multiplicands to nearer to power of 10. This algorithm is same as array multiplier final product can be derived based on array of address. The Urdhava Triyagbhyam Vedic is designed for actual development of multiplication and it is presented in [8] . Here the partial products are generated at the same time. In [8] , 128 × 128 bit Vedic multiplier is implemented.
In [9] , the Urdhava Vedic multiplier is compared with Booth multiplier to analyse their speed and delay. From the results, it is concluded that Urdhava multiplier is superior in delay and power. The speed is improved to the extent of 32% compared with Booth multiplier. The Urdhava multiplier is designed using standard cell approach. The higher bit multiplier is constructed using lower order bits [10] . In [11] , Vedic multiplication is implemented on 8085/8086 microprocessors. In [12] , a multiplication algorithm based on Nikhilam Sutra is designed. In [13] , high speed and low power Vedic multiplier based on Tridhava approach is designed using BEC (Binary-to Excess-one code converter) based carry select adder. Here, instead of two RCA (Ripple Carry Adder), one BEC and one RCA are used. Based on the carry generation, either RCA or BEC outputs are selected. If Cin = “0”, RCA is selected. If Cin = “1”, BEC is selected. From this, power optimal high speed multiplier is designed. In [14] , the Vedic multiplier is designed using modified Carry Select adder. By this, area is reduced by 40% compared with [13] .
In [15] , Vedic multiplier is designed using modified square-root carry select adder (MSQRT-CSA). They compared the performance with various adders like CSA, Carry look-ahead adder (CLA), Square root CSA (SQRT-CSA). Compared with other methods, multiplier with MSQRT-CSA is faster. In [16] , the comparison between traditional binary multipliers is made.
From the survey, Tridhava multiplier can be used for any range of inputs. Different papers were proposed based on the modification in the adders. Though Nikhilam sutra covers all range of inputs, it is efficient when the multiplicands are closer to the multiple of 10. When it is implemented for binary numbers, normally 2’s complement will be taken. The changes are made in the portion of adders. Similarly, Karatsuba algorithm is good for higher order bits. In Karatsuba algorithm, three multipliers are required along with shift operations. But in the proposed method, Karatsuba and Nikhilam sutras are combined. The multiplier required is reduced to one and the number of bit to the multiplier is reduced by two.
2. Principle of Nikhilam Sutra and Karatsuba Algorithm
2.1. Nikhilam Sutra
First, Nikhilam Navatascharam Dashtah sutra means all from 9 and last from 10. The Sutra is well explained for multiplication of decimal numbers. The steps for multiplying decimal numbers using this sutra are given below.
1. The nearest base value of multiplicands is considered. Let us assume the multiplicands are A and B.
2. The remainders of A and B are calculated by subtracting the chosen base value from step 1.
3. The product of remainders of A and B are computed and considered as Right part of final product.
4. The Left part can be computed in three ways. The methods are listed below.
a) The two multiplicands A and B are added and the nearest base value is subtracted from the sum A and B. LP = A + B-10.
b) The Left part is calculated by adding the remainders of A and B with Base value.
c) The remainders of A and B are crossly added with the multiplicands A and B.
5. The Final result is attained by removing the demarcation between LP and RP and concatenating the same.
The remainder is derived using this sutra. Based on the type of the remainder, the algorithm is developed. The two types are:
a) Positive remainder.
b) Negative remainder.
The mathematical expression explaining this sutra is given in Equation 1. Let A and B are the two input numbers. The product P is derived as follows:
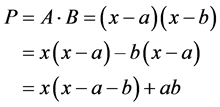 (1)
(1)
Here x acts as base B and it is considered as multiple of 10 depending upon the closeness of multiplicands. The remainders of A and B are known as “a” and “b” respectively. The product “ab” denotes the Right Part (RP). The Left Part (LP) is represented by the first term in (1).
2.2. Karatsuba Algorithm
The Karatsuba algorithm is suited well for multiplying very large numbers. It is a divide and conquer method, in which the number is divided in to Most Significant half and Least Significant half. The multiplication operations are replaced by addition operations and hence the delay of the algorithm is reduced. This algorithm is more efficient when the number of inputs increase. The algorithm is optimal if width of inputs is more than 16 bits.
The numbers are divided as follows
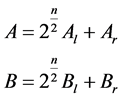 (2)
(2)
where Al, Bl and Ar, Br in Equation 2 are the most significant half and least significant of the numbers A and B respectively and “n” represents the number of bits. Then, the product can be written as,
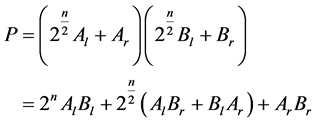 (3)
(3)
From Equation (3), four multiplications and two shift operations are needed. The number is divided equally into two parts. This method is efficient for higher bit length.
3. Proposed Method
In the proposed method, both Nikhilam sutra and Karatsuba algorithm are combined. Using Nikhilam sutra, the remainder is calculated from the nearest value of base 2 by taking 2’s complement. Afterwards, the multiplication is done using Karatsuba algorithm. By doing this, the multiplication required is less.
Let A and B are the numbers and they can be written using Karatsuba algorithm as,
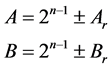 (4)
(4)
The remainders are derived using Nikhilam Sutra in such a manner that the number of bits for remainder is always N-2. Four modules are generated for different combination of removed MSB values. The weight of remainder is reduced. Then the product is derived as follows,
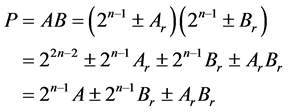 (5)
(5)
while comparing (3) and (5), the proposed algorithm requires only one multiplier. And there is no change the shift operation. The multiplier used in the proposed algorithm requires only N-2 bits. Therefore, proposed work reduces the number of multipliers as well as the number of bits of multiplier. The sign will be selected based on the remainder type of A and B. The example for proposed algorithm is shown below:
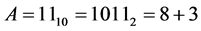
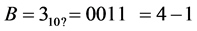
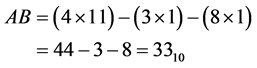
3.1. Algorithm I
Input: A, B
Output: P
Step 1: A and B are the multiplicands with N bits. Their remainders are calculated by removing first two bits and taking 2’s complement for the remaining N-2 bits. (N-1, N-2 = 11)
 and
and 
r1 = complement (A)
r2 = complement (B)
Step 2: Multiplying both remainders using N-2 × N-2 bit multiplier .
.
Step 3: Shifting A by N times (P2)
Step 4: Shifting the remainder r2 by N times (P3)
Step 5: The product can be calculated as,
 (6)
(6)
The proposed architecture for the multiplier for the MSB values 11 is given in Figure 1.
3.2. Algorithm II
Input: A, B
Output: P
Step 1: Calculating remainders for both multiplicands by removing first two bits. If the removed bits are 10, the remainders are determined by taking the numbers without the MSB values. (i.e. N-1, N-2 = 10)
 r1 = A (without first two bits)
r1 = A (without first two bits)
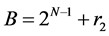 r2 = B (without first two bits)
r2 = B (without first two bits)
Step 2: Multiplying both remainders using N-2 × N-2 bit multiplier (P1).
Step 3: Shifting A by N-1 times (P2)
Step 4: Shifting the remainder by N-1 times (P3)
Step 5: The product can be calculated as,
![]() (7)
(7)
The architecture for the proposed algorithm is shown in Figure 2.
3.3. Algorithm III
Input: A, B N bits
Output: P 2N bits
Step 1: Calculating remainders for both multiplicands by removing first two bits. If the removed bits are 01, the remainders are determined by taking the numbers without the MSB values. (i.e. N-1, N-2 = 10)
![]() r1 = complement (A)
r1 = complement (A)
![]() r2 = complement (B)
r2 = complement (B)
Step 2: Multiplying both remainders using N-2 × N-2 bit multiplier (P1).
Step 3: Shifting A by N-1 times left side (P2)
Step 4: Shifting r2 by N-1 times left side (P3)
Step 5: The product can be calculated as,
![]() (8)
(8)
The architecture for the proposed algorithm is shown in Figure 3.
3.4. Algorithm IV
Input: A, B
Output: P
Step 1: Calculating remainders for both multiplicands by removing first two bits. If the removed bits are 00, the remainders are determined by taking the numbers without the MSB values. (i.e. N-1, N-2 = 10)
![]() r1 = complement (A)
r1 = complement (A)
![]()
Figure 2. Architecture for Algorithm II.
![]()
Figure 3. Architecture for Algorithm III.
![]() r2 = complement (B)
r2 = complement (B)
Step 2: Multiplying both remainders using N-2×N-2 bit multiplier (P1).
Step 3: Shifting A by N-2 times (P2)
Step 4: Shifting r2 by N-2 times (P3)
Step 5: The product can be calculated as,
![]() (10)
(10)
The architecture for this algorithm is shown in Figure 4. From the above said four algorithms, the combined architecture is designed to perform multiplication for binary numbers starting with any value. The combined architecture is shown in Figure 5. In [12] , the detailed explanation is given. For “10” combination, the remainder
![]()
Figure 4. Architecture for Algorithm IV.
derived is positive and for the other combinations the remainders are negative. For negative remainders, the complement should be taken. The input A is shifted N-2, N-1 or N times according to the MSB bits of B. For remainder multiplication, multiplier with N-2 bit is used. The remainder of B is shifted N-1, N-1 or N times. Finally, all the terms added or subtracted according to the algorithm. A simple control circuit is used to select the operation in adder/subtractor module. This architecture is suitable for any input range of inputs. The multiplication is required only when both inputs are nonzero values. The multiplexer is used to reduce the power dissipation when the remainder is zero. In [12] , for the multiplication of remainders, various conventional multipliers are used. By comparing other methods, the proposed method gives high speed. Therefore, in this work, proposed algorithm is applied continuously in the algorithm to increase the speed further.
4. Results
Depending upon the value on Right part, correction is made on left part. In the proposed method, all range of inputs can be given. Karatsuba algorithm is efficient for higher order multipliers. Karartsuba multiplier uses three multipliers based on Equation. (3). But in the proposed method, the numbers of multiplier is reduced to one and number of bits of the multiplier is reduced to N-2. Here, Nikhilam sutra and Karatsuba algorithm are combined to get the high speed. The implementation for various Vedic multipliers is done using Xilinx Spartan 3e kit. In the main module, the proposed multiplier is itself used. The comparison with Vedic multiplier for delay is listed in Table 1. The comparison with conventional methods is also given in Table 2.
The proposed algorithms are written in VHDL and simulated using ModelSim . The simulation result for 32 bit size is shown in Figure 6. We implemented the algorithms of existing and proposed work in Xilinx SPARTAN 3E FPGA. Additionally, implementation result in Xilinx SPARTAN 6 for the proposed method is shown in Table 1. While comparing with SPARTAN 3e, SPARTAN6 delivers high speed but consumes more power. While comparing delay with other methods, the combination of Nikhilam sutra and Karatsuba algorithm gives minimum delay. From Table 1, the delay difference between other methods for higher bits is high. Therefore, this algorithm can be used for high speed applications with wider bit length.
![]()
Figure 5. Combined architecture for multiplier.
![]()
Table 1. Comparison with other vedic multipliers for delay.
![]()
Table 2. Delay comparison with other conventional binary multipliers.
![]()
Figure 6. Simulation waveform for the multiplier with 32 bit.
5. Conclusion and Future Work
In this research paper, successive approximation of Vedic multiplier is proposed for high speed applications. The algorithm of Karatsuba is modified to reduce the number of multipliers required in the calculation. Instead of splitting the binary number into half, the number is split based on remainder value. The remainder is calculated using Nikhilam Sutra such that the number of bits is reduced to N-2. By combining Nikhilam Sutra and Karatsuba algorithm, the number of bits to the multiplier is reduced. Four modules were created based on remainders. From the results’, it is clear that the proposed method produces output faster than other methods. This hybrid multiplier is best suited for multiplying large numbers in high speed applications.