New Types of Lambda-Transitive and Weakly Lambda-Mixing Sets

Mohammed Nokhas Murad Kaki^1,2

¹California University, Los Angeles, USA.
²Faculty of Science, University of Grant-Chester, London, UK.

DOI: 10.4236/oalib.1102506                

Abstract

This research paper is intended as a survey article on new types of mixing, weakly mixing, transitive and chaotic sets in a topological dynamical system. I mention here some new kinds of chaotic maps and chaotic sets and indicate their connection between them. Chaotic behavior is a manifestation of the complexity of nonlinear system. There are several different definitions of topological transitive sets and chaos, which describe the complexity of systems in different aspects. The present work mainly deals with some new types of these definitions. In this project, I explain the main new ingredients of new type of chaotic sets and transitive sets in a given topological space. Further I illustrate relationship between the new and basic definitions of sets are given.

Keywords

Topological λ-Transitive sets, λ-Mixing, Weakly λ-Mixing Sets and Chaos

Subject Areas: Dynamical System

1. Introduction

We will consider a system given by a locally compact Hausdorff space (phase space) X and λ-irresolute map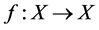. A point 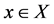“moves,” its trajectory being the sequence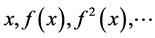, where 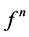is the nth iteration of f. The point 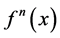is the position of x after n units of time. The set of points of the trajectory of x under f is called the orbit of x, denoted by. As a motivation for the notion of topological transitivity of one may think of a real physical system, where a state is never given or measured exactly, but always up to a certain error. So instead of points one should study λ-open subsets of the phase space and describe how they move in that space. If for instance the λ-type minimality of 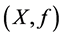is defined by requiring that every point 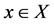visits every λ-open set V in X (i.e., 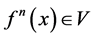for some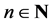) then, instead, one may wish to study the following concept: every nonempty λ-open subset U of X visits every nonempty λ-open subset V of X in the following sense: for some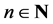. If the topological system 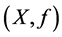has this property; then it is called topologically λ-type transitive. We also say that f itself is topologically λ-transitive.

In this paper, new types of topologically λ-type transitive sets are introduced and studied. This is intended as a survey article on transitive sets in a system given by a λ-irresolute self-map on a topological space. On one hand it introduces postgraduate students to the study of new types of topological transitive sets and gives an overview of results on the topic; but, on the other hand, it covers some of the recent developments of mathematical science, technology, electronic and computer science. I introduced and defined a new type of transitive sets called λ-type transitive set and some of its properties are investigated. Relationships with some other types of transitive sets are given. I list some relevant properties of the λ-type transitive set. I have proved that every λ-type transitive set is transitive set but the converse not necessarily true. A topologically λ-type transitive set does not partition into nonempty λ-closed subsets. If A is a topologically λ-type transitive set, then there does not exist nonempty disjoint λ-closed subsets B and C of A such that. Every topologically transitive set is nonempty λ-closed and invariant. The set of all λ-cluster points is called the λ-closure of A and is denoted by A point x ∈ X is said to be a λ-interior point of a subset A ⊂ X if there exists a λ-open set U containing x such that U ⊂ A. The set of all λ-interior points of A is said to be the λ-interior of A and is denoted by, [1] - [3] .

2. Preliminaries and Definitions

To study the dynamics of a self-map means to study the qualitative behavior of the sequences as n goes to infinity when x varies in X, is the position of x after n unit of time, where denotes the composition of f with itself n times.

Definition 2.1. [4] By a topological system I mean a pair where X is a locally compact Hausdorff space (the phase space), and is a continuous function. The dynamics of the system is given by and the solution passing through x is the sequence.

Definition 2.2. Let, then the set is called an orbit of x under f, so is the set of points which occur on the orbit of x at some positive time, and the sequence is called the trajectory of x.

The set of limit points of the orbit is called the -limit set of x, and is denoted by A subset D of X is f-invariant if A non-empty closed invariant subset D of X is minimal, if for every A point is minimal if it is contained in some minimal subset of X.

For a point we say that f is λ-type open at x if for every open set U containing x, for a subset we say that f is λ-type open on A, if f is λ-type open at x for every Note that if f is open at x then it is λ-type open at x but not conversely.

Definition 2.3. [5] A function is called λ-irresolute if the inverse image of each λ-open set is a λ-open set in X.

Proposition 2.4. Let be a map, where X, Y are λ-compact, second countable, Hausdorff spaces. If for each there exists a λ-open set U containing p such that is λ-irresolute, then f is λ-irresolute.

Proof: Suppose that for every there exists a λ-open set U such that is λ-irresolute. So there is a cover with this property. Consider a λ-open set. Note that so which is λ-open since f is λ-irresolute.

Definition 2.5. (1) Let be a topological space, be λ-irresolute map, then the set is called λ-type transitive set if for every pair of non-empty λ-open sets U and V in X with and there is a positive integer n such that_.

(2) A topological system is λ-type chaotic if for every λ-open pair of not empty subsets there are a periodic point and such that

Note that:

(1) Every λ-type transitive set is transitive set but not conversely.

(2) Every λ-type transitive map is transitive map but not conversely.

(3) The reason of the foregoing statements is that the map defined on the λ-transitive set is λ-transitive map. For more knowledge see [6] .

Definition 2.6 (1). Let be a topological space, be λ-irresolute map, then the set is called topologically λ-mixing set if given any nonempty λ-open subsets with and then such that for all

(2) A λ-closed set is called a weakly λ-mixing set of if for any choice of nonempty λ-open subsets of A and nonempty λ-open subsets of X with and there exists

n ∈ N such that and

Proposition 2.7. If A is a weakly λ-mixing set of, then A is a λ-type transitive set of.

3. λ-Type Transitive Sets and Topological λr-Conjugacy

In the present section, I will introduce and define λ-type transitive sets. I will study some of their properties and prove some results associated with these new definitions. Some properties and characterizations of such sets are investigated.

A homeomorphism is a bijective continuous map with continuous inverse. More explicitly, to say that “a bijective mapping f of X onto Y is a homeomorphism” means that “is open if and only if is open”.

Definition 3.1. A function is called λr-homeomorphism if f is λ-irresolute bijective and is λ-irresolute. More explicitly, to say that “a bijective mapping f of X onto Y is λr-homeomor- phism” means that “is λ-open if and only if is λ-open”.

Definition 3.2. Two topological systems, and, are said to be topologically λr-conjugate if there is λr-homeomorphism such that I will call h a topological λr-conjugacy.

Then I have proved some of the following statements:

1) The maps f and g have the same kind of dynamics.

2) is a topological λr-conjugacy.

3)

4) A set B is λ-mixing set if and only if is λ-mixing set.

5) A set B is weakly λ-mixing set if and only if is weakly λ-mixing set.

Proposition 3.3. If are λr-conjugated by the λr-homeomorphism then for all y ∈ Y the orbit is λ-dense in Y if and only if the orbit of h(y) is λ-dense in X.

Proof: Suppose that are maps λr-conjugate via such that , then if for all y ∈ Y the orbit is λ-dense in Y, let be a nonempty λ-open set. Then since h is a λr-homeomorphism, is λ-open in Y, so there exists with. From it follows that so that is λ-dense in X. Similarly, if is λ-dense in X, then is λ-dense in Y.

If h is not λr-homeomorphism but only λ-irresolute surjection (a semi-λr-conjugacy), then the orbit is λ-dense in Y implies the orbit of h(y) is λ-dense in X, but not conversely.

Proposition 3.4. if are λr-conjugate. Then,

(1) T is λ-type transitive subset of X is λ-type transitive subset of Y;

(2) T is λ-mixing subset of X is λ-mixing subset of Y.

Proof (1).

Assume that are topological systems which are topologically λr-conjugated by.Thus, h is λr-homeomorphism (that is, h is bijective and thus invertible and both h and are λ-irresolute) and

Suppose T is λ-type transitive subset of X. Let A, B be λ-open subsets of Y with and (to show for some). are λ-open subsets of X since h is an λ-irresolute.

Then there exists some n > 0 such that since T is λ-type transitive subset of X, with and. Thus (as implies).

Therefore, implies since is invertible. So h(T) is λ-type transitive subset of Y.

Proof (2).

We only prove that if T is topologically λ-mixing subset of Y then h⁻¹(T) is also topologically λ-mixing subset of X. Let U, V be two λ-open subsets of X with and. We have to show that there is N > 0 such that for any n > N, and are two λ-open sets since h is λ-irresolute with and. If the set T is topologically λ-mixing then there is N > 0 such that for any n > M, So. That is and for,. Thus, since, so that, , and we have that is So, h⁻¹(T) is λ-mixing set.

Proposition 3.5. Let be a topological system and A be a nonempty λ-closed set of X. Then the following conditions are equivalent.

1) A is a λ-transitive set of.

2) Let V be a nonempty λ-open subset of A and U be a nonempty λ-open subset of X with. Then there exists such that.

3) Let U be a nonempty λ-open set of X with. Then is λ-dense in A.

Note that for any,; the n^th inverse image of A.

Theorem 3.6. Let be topological system and A be a nonempty λ-closed invariant set of X. Then A is a λ-type transitive set of if and only if is λ-type transitive system.

Proof:

Þ) Let be two nonempty λ-open subsets of A. For a nonempty λ-open subset of A, there exists a λ-open set U of X such that. Since A is a λ-type transitive set of, there exists n ∈

N such that Moreover, A is invariant, i.e., , which implies that Therefore, , i.e.. This shows that is λ-type transitive system.

Ü) Let be a nonempty λ-open set of A and U be a nonempty λ-open set of X with Since U is a λ-open set of X and, it follows that U ∩ A is a nonempty λ-open set of A. Since is topologically λ-type transitive system, there exists n ∈ N such that which implies that. This shows that A is a λ-type transitive set of.

4. Conclusions

There are the following results:

Proposition 4.1. Every topologically λ-transitive set is transitive set but not conversely.

Proposition 4.2. If are -conjugate. Then,

(1) T is λ-type transitive set in X if and only if is λ-type transitive set in Y;

(2) T is λ-type mixing set in X if and only if is topologically λ-mixing set in Y.

Definition 4.3. Let be a topological space and be λ-irresolute map, then the set is called topologically λ-mixing set if, given any nonempty λ-open subsets with and then such that for all

Definition 4.4. A λ-closed set is called a weakly λ-mixing set of if for any choice of nonempty λ-open subsets of A and nonempty λ-open subsets of X with and

there exists n ∈ N such that and

Proposition 4.5. If A is a weakly λ-mixing set of, then A is a λ-type transitive set of.

Proposition 4.6. Let be a topological system and A be a nonempty λ-closed set of X. Then the following conditions are equivalent.

1) A is a λ-transitive set of.

2) Let V be a nonempty λ-open subset of A and U be a nonempty λ-open subset of X with. Then there exists such that.

3) Let U be a nonempty λ-open set of X with. Then is λ-dense in A.

Theorem 4.7. Let be topological system and A be a nonempty λ-closed invariant set of X. Then A is a λ-type transitive set of if and only if is λ-type transitive system.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Maki, H. (1986) Generalized Λ-Sets and the Associated Closure Operator. The Special Issue in Commemoration of Prof. Kazusada IKED’s Retirement, 1 October, 139-146.
[2]	Arenas, F.G., Dontchev, J. and Ganster, M. (1997) On λ-Sets and the Dual of Generalized Contiuity. Questions and Answers in General Topology, 15, 3-13.
[3]	Caldas, M. and Jafari, S. (2005) On Some Low Separation Axioms via λ-Open and λ-Closure Operator. Rendiconti del Circolo Matematico di Palermo, 54, 195-208. http://dx.doi.org/10.1007/BF02874634
[4]	Murad, M.N. (2013) New Types of Λ-Transitive Maps. International Journal of Research in Electrical and Electronics Engineering, 2, 19-24.
[5]	Caldas, M., Jafari, S. and Navalagi, G. (2007) More on λ-Closed Sets in Topological Spaces. Revista Colombiana, 41, 355-369.
[6]	Murad, M.N. (2014) New Types of Chaotic Maps on Topological Spaces. International Journal of Electrical and Electronic Science, American Association for Science and Technology, 1, 1-5.