Numerical Analysis of the Effect of Temperature and External Optical Feedback Variation on the Output Characteristics of External Cavity Semiconductor Laser Based Fiber Bragg Gratings ()
Received 17 November 2015; accepted 3 December 2015; published 8 December 2015
Subject Areas: Electric Engineering
1. Introduction
With a rapid increase in demand for large optical transmission capacity, wavelength-division multiplexing (WDM) systems have become essential as a huge and high-speed data transmission method. Thus far, WDM systems up to 50-GHz channel spacing have already been used [1] - [7] . However, in the near future, much larger transmission capacity would be required with further progress of information technology revolution. To satisfy this requirement, dense WDM (DWDM) systems with narrower channel spacing will be indispensable [3] . In WDM systems, coherent light source with a more accurate and more stable lasing wavelength is required [4] . Distributed feedback (DFB) semiconductor laser diodes are widely used in these systems as single-mode laser sources. However, tuned DFB lasers are expensive because of the relative bad yield rate. Since the emission wavelength of a DFB laser depends heavily on temperature and injection current [5] - [7] , it is difficult to sort out DFB laser modules, which are tuned at predetermined wavelength. In addition, the improvements in the laser manufacture allow today operating un-cooled directly modulated lasers over abroad temperature range. Since a significant reduction in the optical system can be achieved without the need to control the temperature of the laser. Un-cooled directly modulated laser has been regarded as one of the key technologies for optical networks in the future.
On the other hand, the semiconductor laser diodes (SLDs) are extremely sensitive to external optical feedback (OFB), which arises in practical applications due to back reflections depending on the feedback level [8] . In contrast, much cheaper Fabry-Perot laser diodes (FP-LDs) are not very stable and spectrally not narrow. Their multi-mode operation and strong dependence on temperature and supply current [5] make them not too effective for using as relatively stable sources in the WDM applications. One way of improving the mode selectivity is to make the feedback frequency-dependent, so that the cavity loss is different for different longitudinal modes [9] - [13] .
In external cavity semiconductor laser based fiber Bragg gratings (ECSL-FBGs), the emission wavelength is dependent only on Bragg wavelength and independent of chip temperature or injection current. Precise adjustment of the Bragg wavelength of a fiber grating (FG) is available compared with the emission wavelength of DFB lasers. So the lasing wavelength in ECSL-FBGs model is highly stable with temperature and current. In addition, the Bragg wavelength can be controlled more precisely than that of the DFB lasers in the actual fabrication process. As a result, the ECSL-FBGs model realizes much better wavelength stability and controllability [14] - [20] . Therefore, ECSL-FBGs model is promising as a high stable and low-cost light source of a future DWDM system compare with other laser models.
To date, many experimental and theoretical studies have been reported on the FGFP laser [1] [4] [21] . However, in most of these studies, the temperature effect is not taken into account. In addition, they assumed that the external cavity diode laser was under strong OFB; i.e. the effect of external OFB was not investigated in weak and moderate levels. Thus, full visualizations of the temperature and the external OFB effects on the output characteristics were not provided. Therefore, an accurate knowledge on the effects of these parameters is very important for avoiding ECSL-FBGs to operate in inoperable regime.
The paper is structured as follows: The external cavity semiconductor laser model based fiber a Bragg grating (ECSL-FBGs) is given in the next section. Section 3 presents the temperature dependence for ECSL-FBGs model output power with external OFB. The simulation results are discussed in Section 4 followed by the conclusion.
2. External Cavity Semiconductor Laser Model Based Fiber Bragg Gratings
The external cavity semiconductor laser model based fiber Bragg gratings (ECSL-FBGs) consists of three main sections as shown in Figure 1(a). The first section is the Fabry-Perot laser diode (FP-LD) of length Ld. It is assumed that the reflectivity of the chip front facet (Ro) is very low to suppress FP mode oscillation and to stabilize the external cavity mode, while the rear facet has high reflectivity (R1). The second section is a fiber of length Lext; and the third is the FBGs with reflection coefficient of rFBG. The FP-LD and the FBGs are optically coupled through a coupling lens, and thus external cavity is constructed. The temperature dependence (TD) to the photons round-trip time inside the internal and the external cavity are τd(T) = 2nd(T)Ld/c and τe(T) = 2Lextnext(T)/c, respectively, where c, is the velocity of the light in the vacuum, nd(T) is the TD group refractive index of the FP-LD, and next(T) is the TD fiber refractive index.
This configuration may be conveniently analyzed as a simple two-mirror laser structure (Figure 1(b)) by replacing the FP diode laser output facet reflectivity Ro by a complex-valued effective reflection coefficient Ref [14] .
![]()
Figure 1. (a) Schematic structure of FGFP laser; (b) Simplified configuration [14] .
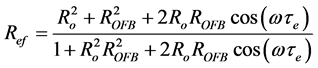 (1)
(1)
where 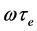 is the phase of the reflected light that travels through the external cavity and
is the phase of the reflected light that travels through the external cavity and 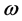 is the laser angular frequency. In Equation (1),
is the laser angular frequency. In Equation (1), 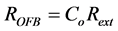 is the amount of OFB reflection coupled into FP-LD, where
is the amount of OFB reflection coupled into FP-LD, where 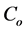 is the amplitude coupling coefficient between the FP-LD and the fiber grating (FG), and
is the amplitude coupling coefficient between the FP-LD and the fiber grating (FG), and 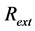 is the power reflectivity of FG defined as [21] [22]
is the power reflectivity of FG defined as [21] [22]
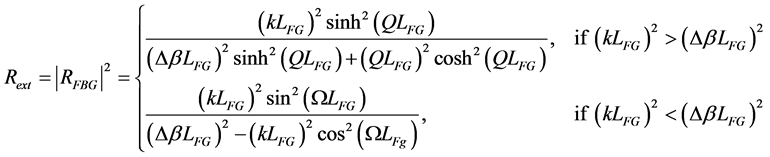 (2)
(2)
where 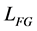 is the grating length,
is the grating length, 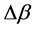 is the wavelength detuning, k is the coupling strength,
is the wavelength detuning, k is the coupling strength, 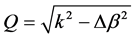 ,
,
and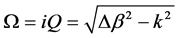 . The phase coefficient for reflection light
. The phase coefficient for reflection light  is derived from the differential equations in [22] and is given by
is derived from the differential equations in [22] and is given by
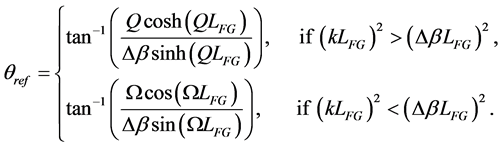 (3)
(3)
By considering the phase change introduced by the optical filter in Equation (1), ![]() can be rewritten as
can be rewritten as
![]() (4)
(4)
3. Output Characteristics of ECSL-FBGs Laser Model
The temperature dependence (TD) of threshold current Ith,fe(T) of ECSL-FBGs laser under the effect of external OFB can be written as [11] [13]
![]() (5)
(5)
where q is the electron charge, V is the FP-LD active region volume, Anr describes the non-radiative recombination rate due to traps or surface states, C(T) is the TD Auger process, B is the radiaitive recombination coefficient, and Nth,fe(T) is the TD carrier density at the threshold condition. The Nth,fe(T) can be represented by modifying the well-known expression in [13] as
![]() (6)
(6)
where![]() ,
, ![]() , and
, and ![]() are the TD parameters that is known as transparency carrier density, gain constant, and photon life time (with the external OFB effect), respectively.
are the TD parameters that is known as transparency carrier density, gain constant, and photon life time (with the external OFB effect), respectively. ![]() denotes the confinement factor, and
denotes the confinement factor, and ![]() is the TD group velocity. The TD parameters are assumed to vary with the temperature according [23]
is the TD group velocity. The TD parameters are assumed to vary with the temperature according [23]
![]() (7)
(7)
where Xo is the initial value found at the reference temperature (To), which is considered at the room temperature (25˚C). Since the external OFB only affects on the photon lifetime in Equation (6), ![]() can be modeled as
can be modeled as
![]() (8)
(8)
where ![]() is the TD total cavity loss that is defined as [11] [13] .
is the TD total cavity loss that is defined as [11] [13] .
![]() (9)
(9)
where ![]() is the TD internal cavity loss, and the term
is the TD internal cavity loss, and the term ![]() represent the mirror loss (
represent the mirror loss (![]() )
)
under the effect of external OFB. Based on Equations (1)-(9), the TD threshold carrier density ![]() can be expressed as
can be expressed as
![]() (10)
(10)
Equation (10) gives a general expression for the TD threshold carrier density under the effect of external OFB, which is used to calculate the net rate of stimulated emission in the ECSL-FBGs laser active region. Finally, the TD of the output power from the front face of ECSL-FBGs laser model under the effect of the external OFB corresponding to the selected Bragg wavelength can be written as
![]() (11)
(11)
where
![]() (12)
(12)
4. Simulation Analysis
In this study, the output characteristics of ECSL model with uniform FBGs operating at 1550 nm wavelength is analyzed. The parameters of the model used in the analysis are shown in Table 1. All these values are fixed throughout this study, except otherwise is stated.
Figure 2 shows the effect of temperature (T) and effective reflectivity (Ref) variations on the total cavity loss (![]() ) of ECSL-FBGs model. As shown, with increasing the Ref value;
) of ECSL-FBGs model. As shown, with increasing the Ref value; ![]() has reduced sharply. This reduction is due to increase the multi-reflection inside the laser cavity which leads to increase the total cavity gain; thus reducing
has reduced sharply. This reduction is due to increase the multi-reflection inside the laser cavity which leads to increase the total cavity gain; thus reducing![]() . Mathematically, this result is consistent with that which given in Equation (9). No From other side, there no effected change in
. Mathematically, this result is consistent with that which given in Equation (9). No From other side, there no effected change in ![]() with the ambient temperature changes from 15˚C to 30˚C. This is because the emission wavelength of ECSL-FBGs model is determined basically by the FBG which characterized by a high degree of stability with temperature variation.
with the ambient temperature changes from 15˚C to 30˚C. This is because the emission wavelength of ECSL-FBGs model is determined basically by the FBG which characterized by a high degree of stability with temperature variation.
![]()
Table 1. Parameters of FGFP at reference temperature To (To = 25˚C) [14] - [20] .
![]()
Figure 2. Effect of temperature variations and effective reflectivity on total cavity loss of ECSL-FBGs laser model.
Figure 3 show the effect of temperature (T) and effective reflectivity (Ref) variations on ECSL-FBGs laser photon lifetime (![]() ). As depicted, with increasing the Ref level,
). As depicted, with increasing the Ref level, ![]() increases almost linear. This is due to decreasing
increases almost linear. This is due to decreasing ![]() with Ref as shown in Figure 2. Based on Equation (8),
with Ref as shown in Figure 2. Based on Equation (8), ![]() is strongly depend inversely on the value of
is strongly depend inversely on the value of![]() . Thus, any reduction in the
. Thus, any reduction in the ![]() value leads gradually to increase
value leads gradually to increase![]() . Conversely, there is no effected effect for temperature variation on
. Conversely, there is no effected effect for temperature variation on ![]() similarly as given in Figure 2.
similarly as given in Figure 2.
The effect of temperature (T) and effective reflectivity (Ref) variations on threshold carrier density (![]() ) is shown in Figure 4. According to Equation (10),
) is shown in Figure 4. According to Equation (10), ![]() is determined by the internal cavity loss and external
is determined by the internal cavity loss and external
![]()
Figure 3. Effect of temperature (T) and effective reflectivity (Ref) variations on ECSL-FBGs laser photon lifetime.
![]()
Figure 4. Effect of temperature (T) and effective reflectivity (Ref) variations on ECSL-FBGs laser threshold carrier density.
OFB mirror loss, as well as by the TD of ![]() and
and![]() , respectively. In this case, by increasing the external OFB level, the total cavity loss will reduce (as shown in Figure 2) which leads to increment in
, respectively. In this case, by increasing the external OFB level, the total cavity loss will reduce (as shown in Figure 2) which leads to increment in![]() . In contrast, there is a little effect in
. In contrast, there is a little effect in ![]() with temperature variations.
with temperature variations.
Figure 5 shows the dependence of ECSL-FBGs laser threshold current (![]() ) on temperature variations (T) and external OFB. As shown, with increasing the effective reflectivity (Ref) level, the
) on temperature variations (T) and external OFB. As shown, with increasing the effective reflectivity (Ref) level, the ![]() reduced. This effect we can explain based on Equation (5), where by increasing Ref, the
reduced. This effect we can explain based on Equation (5), where by increasing Ref, the ![]() will decrease leads to increment the
will decrease leads to increment the ![]() as shown in Figure 2 and Figure 4, respectively. Any reduction in the
as shown in Figure 2 and Figure 4, respectively. Any reduction in the ![]() results in decreasing
results in decreasing![]() . In contrast, there is a significant impact in
. In contrast, there is a significant impact in ![]() with the variations of T under the condition of high level for the Ref. For example,
with the variations of T under the condition of high level for the Ref. For example, ![]() equal to 14 mA and increasing to 14.6 mA with increases T from 25˚C to 30˚C
equal to 14 mA and increasing to 14.6 mA with increases T from 25˚C to 30˚C
![]()
Figure 5. Effect of temperature variations and effective reflectivity (Ref) on ECSL-FBGs laser threshold current.
![]()
Figure 6. Effect of the temperature (T) and the effective reflectivity (Ref) variations on ECSL-FBGs laser output power.
for![]() . While; by increasing the Ref to 0.9, the
. While; by increasing the Ref to 0.9, the ![]() decreased to 8.2 mA for T variations from 25˚C to 30˚C.
decreased to 8.2 mA for T variations from 25˚C to 30˚C.
Finally, Figure 6 shows the effect of the temperature variations and the effective reflectivity (Ref) on ECSL- FBGs laser output power. The ECSL-FBGs laser model with threshold current (![]() ) of 8 mA and slope efficiency of 0.19W/A. The output power (Pout,fe) of ECSL-FBGs laser model is investigated based on Equation (11). As shown, by increasing Ref, the Pout,fe increase due to reduce the total fluctuation inside the laser cavity. As an example, by injecting current of 60 mA, the Pout,fe increasing to 10 mW at Ref = 0.9. In addition, by changing the temperature; the Pout,fe not affected strongly due to the highly wavelength stability of grating fiber with temperature variations.
) of 8 mA and slope efficiency of 0.19W/A. The output power (Pout,fe) of ECSL-FBGs laser model is investigated based on Equation (11). As shown, by increasing Ref, the Pout,fe increase due to reduce the total fluctuation inside the laser cavity. As an example, by injecting current of 60 mA, the Pout,fe increasing to 10 mW at Ref = 0.9. In addition, by changing the temperature; the Pout,fe not affected strongly due to the highly wavelength stability of grating fiber with temperature variations.
5. Conclusion
A numerical study on the effect of the temperature (T) variations and external OFB on output characteristics of ECSL-FBGs laser model is successfully conducted. It has been shown that, through simulation, the output characteristic of ECSL-FBGs laser model is extremely sensitive to the external OFB level. On the other hand, results show that there is no effected effect for temperature variation on the model output. This is because, in this study, the temperature dependence (TD) of laser characteristics is calculated according to TD of laser parameters instead of using the well-known Pankove relationship [4] [14] - [20] . In this case, we have taken into account the thermal effect of each affecting parameter on the model instead of using an empirical equation for temperature analysis. Thus, by this way the simulation results are more accurate than previous cases.