Neural and Spinal Modules in Implementation of a Simple Ballistic Movement ()
Received 24 March 2016; accepted 16 July 2016; published 19 July 2016

1. Introduction
This paper is involved with the formulation of rudimentary quick human movements. Examples can be cited in softball [1] [2] , kicking a soccer ball [3] - [5] , jumping off the ground [6] - [8] and performing a back somersault [9] - [11] . These movements are also referred to as ballistic movements [12] [13] . The ballistic movement, as formulated here, may be triggered by and synchronized with external events, may have to be reversed in time [14] [15] , and requires three consecutive phases in time. The three time intervals and the required central processing in each are vital to the execution of the movement. The timing and time event processing [16] - [19] may be carried out in the hippocampus [20] [21] , the cerebellum [22] , basal ganglia, and the reticular formation [23] .
The dynamics can be derived using different principles [24] [25] . Substantial research that merits a review of its own has been carried out by Soechting and colleagues [26] - [29] on the human arm. Iqbal and Roy [30] present a sagittal neuromusculoskeletal system. Simpler systems also have been proposed [31] . Three degrees of freedom are assumed at every joint here. More physiologically realistic constraints at the elbow and the wrist [32] [33] could be considered and related to experimental observations [34] [35] .
The three-link arm is equipped with 15 pairs of muscles and has already been used in some upper extremity research [36] - [38] . A virtual neuromusculoskeletal system is considered in [39] . A model, suitable for simu- lation has been formulated [40] . A model, emphasizing joint coordination, is presented in [41] . Studies of fingers, the palm of the hand, and forearm are carried out in [42] . Mathematical investigations of the arm and the kinematic issues are respectively addressed in [43] [44] . More physiologically accurate moment arms of the muscles, muscle masses, and muscle lengths and moment arms are respectively investigated in [45] - [47] .
The underlying philosophy of control presented here is to centrally command the arm to execute a specific maneuver. Further, it is intended that the three-link model be a building block in larger skeletal systems that would be composed of many such three-link modules. This philosophy of modeling and control merits further study of its own and is not undertaken here.
The ballistic movement from one equilibrium point to a second is brought about by an initial phase of acceleration, a second phase of coasting and a third phase of deceleration and stop. Co-activation [48] guarantees stability. Smoothness of motion and fast stop are implemented by spinal reflexes. Similar strategies of control are cited in the robotic field [38] and for anthropomorphic robots [49] . A number of hypotheses [30] [50] , experimentally-based observations [51] , and animal observations [52] - [54] support the model presented here.
In the present paper, the trajectory of the desired movement of the arm is articulated in the Central Nervous System (CNS) by specifying the nine Bryant angles [55] - [57] as functions of time. Further, the shape of the trajectories here is consistent with Kornhuber’s [51] [58] hypotheses that simple point-to-point movements are ramp type and that the basal ganglia is responsible for the synthesis of the linear trajectories [55] [59] [60] . As stated before, three phases of central and peripheral activity are required. A simple cerebellum model [61] takes care of programming the turning on and off the agonist and antagonist activations [62] and the necessary spinal reflexes [63] . Simple models of the needed basal ganglia and the cerebellum are presented. Specifically, the presentation here is consistent with Evarts’ formulation [64] [65] (namely, the attention set and attention mechanisms [66] ).
Timing is a major component of the implementation of fast movements, motivated by internal events or conditioned by external events, in activities such as sports. More complex related events in the CNS are storage and recall of information, delaying or advancing events in time, synchronizing, time scaling and reversing events in time. Three-phase timed events in tapping, stepping and rocking [67] , are part of a longer sequence in dance. Other examples are compression or expansion of signals in time, i.e, speeding up a movement or slowing it down. A timed event may be part of a pattern generator or an oscillator.
In a dynamic system, described by an Artificial Neural Network (ANN) or a differential equation [68] , a set of programmable gains control the behavior of the system as in cardiac myocytes [68] [69] and ( [70] , page 250). A majority of such motor functions in living systems are described qualitatively, e.g., ( [54] , Figs 41-14 and 42-5). Examples of conditioning and measurement of duration of events that need to be timed and the neural processing needed for timed events are presented in [71] [72] . A description of the conditioned reflex is provided in ( [20] , chapter 10) and in ( [73] , chapter 13).
Chemical agents and neuro-transmitters induce the needed gain changes in many instances. Serotonin is one agent known to increase the duration of action potentials in abdominal and pleural sensory neurons of Aplysia ( [70] , page 250). It inhibits and delays repolarization due to potassium channels. Serotonin may further decrease a voltage-dependent delayed rectifying potassium current and thus prolong the action potential ( [70] , page 254).
Internal timed events are involved in motor learning, natural reflexes, and tight input-output coupling [34] [52] [74] [75] . Psycho-physical experiments [76] point to processing in the CNS that is governed by laws of physics [77] [78] . Arbib ( [79] , page 53) discusses leaky integrators as more realistic physical models of neurons. In Arbib’s view, a neuron circuit with a long time constant becomes an approximate integrator and, hence, a basic memory element. Doeringer and Hogan [50] have estimated the neural transmission delay in the spinal reflex loop of the upper extremity to be in the order of 30 ms, with a transfer function that has a frequency range of zero to less than 2 Hz. An inverse compensator is proposed for the delay, a form of predictor [80] . Predictors are also discussed in ( [81] , page 62) and [82] .
A single trajectory of force or motion [54] [77] can be stored in a tapped delay line [83] [84] , compatible with the structure of short-term memory ( [20] [77] , page 86 and chapter 9). The fading away of the information can be modeled as attenuation in a lossy delay line. Larger units of the CNS function can be envisioned that are involved in signal generation and processing. Time scaling and piece-wise linear signals are examples. Time scaling involves producing a slower or faster movement.
Timed events are also involved when the CNS has to relate internal decisions to external events. Timing [85] - [87] relative to an external cue or alarm could involve associative learning ( [54] , Chapter 65). Timing is also involved in mechanisms of attention [64] , preparation for a movement or in a motor set [73] . The role of the hippocampus in time reversal of movement has been noted [20] [21] , According to Foster and Wilson [14] , while rats rest after running a maze, their brains replay the movements in reverse. The idea of reversing events in time is a case of spatial synchronization of internal action with external events that is expounded later in Section 4 of the paper.
There are cases in the CNS where different sensory neurons fire in synchrony ( [54] , chapter 30, and [88] ). A simple example of this is the eye-blink experiment [89] . In this experiment [20] [90] , blowing a puff of air in a rabbit’s eye will cause the rabbit to blink [90] . Grethe and Thompson [90] review and compare models of this synchronization. Tapped delay lines of different lengths [78] [91] [92] were proposed. Artificial Neural Net- works (ANNs) can mimic the coincidence model of Buhusi and Meck [93] , granule cells begin to oscillate at the start of the conditioned stimulus, and then the outputs of these granule cells are recorded at the time of the stimulus. Nicholls et al. ( [94] , page 552) discuss, for medullary neurons that generate the respiratory rhythm in neonatal opossum, the location of synapses and the incremental time delays that are important in temporal processing and signal shaping. Simultaneous patterns may have to be recalled from storage or from pattern generators ( [70] , chapter 17). Two alternative schemes to generate patterns are by linear filters and neural oscillators [60] [68] [95] - [97] . The transient outward current in the bag cell neuron is shown to contain one exponential function of time with a time constant of 76 ms, and, under the influence of cyclic AMP, to contain a second exponential of a much faster decay (and, hence, a rationale for a second order system). Neuro-trans- mitters change the shape of an action potential ( [70] , page 249), suggesting the possibility of filtering and pro- cessing mechanisms that are implicit. In this case, that mechanism was the narrowing of the action potential pulse in the dorsal root ganglion of a chick. Other patterns are involved in voluntary movements or in elicited maneuvers [98] [99] or slipping and sliding [100] [101] .
For ease of presentation, afferent and efferent neural transmission delays are ignored in this paper [102] [103] . Spinal reflex delays are included because they are crucial to the stability of the ballistic movement. Spinal reflexes and spinal cord injury [104] - [106] , as a whole, merit more serious consideration that is not warranted here. A rudimentary spinal reflex for controlling forces of contact in pushing or pulling is considered in [107] . A simple spinal reflex is modeled here and more physiologically accurate models [80] [108] [109] remain to be included and investigated in the future. Similarly, it is assumed that gravity is fully compensated and does not affect the motion directly [110] . All discussions, models and formulas derived and developed here are limited to the simple ballistic movement and should not be construed to represent universal models of the cerebellum, the basal ganglia, the reticular formation, or the hippocampus.
The structure of the paper is as follows. The dynamics and control of the three-segment arm are briefly discussed in Section 2. The modeling of fast movements is presented in Section 3. The timing issues and central neural structures for the ballistic movement, its reversal in time and conditioning are presented in Section 4. Simulations of a movement (similar to one in throwing a softball) with and without delays in the spinal reflex path are presented in Section 5. Discussions and conclusions follow in Section 6.
2. Arm Dynamics and Stability
The derivation of the dynamics of the three-link arm system are briefly sketched here. The formulation starts with the free body equations. The 18-dimensional vector Z represents the nine translational position states 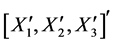 and the nine rotational Bryant angles
and the nine rotational Bryant angles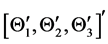 . The arm is assumed to be connected to an stationary torso (the inertial coordinate system) and, as a consequence, all translational degrees of freedom are eliminated to derive the systems equations in terms of the rotational degrees of freedom. The 18-dimensional state space equations of the system are symbolically written here:
. The arm is assumed to be connected to an stationary torso (the inertial coordinate system) and, as a consequence, all translational degrees of freedom are eliminated to derive the systems equations in terms of the rotational degrees of freedom. The 18-dimensional state space equations of the system are symbolically written here:
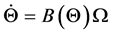 (1)
(1)
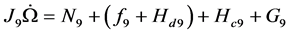 (2)
(2)
There are four nine-vector terms of the second equation. All muscular inputs are included in vector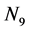 . The are two nonlinear terms:
. The are two nonlinear terms: 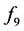 and
and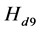 . The centrifugal term is
. The centrifugal term is 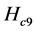 and the gravity term is
and the gravity term is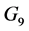 . The steps in the definition and the derivation of these vectors are given in [8] [66] .
. The steps in the definition and the derivation of these vectors are given in [8] [66] .
Stability is achieved by the simultaneous co-activation of agonist-antagonist pairs of muscles by at least three pairs at every joint [111] - [113] . The co-activation produces sufficient position and velocity feedback to bring about stability in the vicinity of the vertical equilibrium position. It can be shown that with no limitation on the amplitudes of the feedback, the system can be globally stabilized [114] . Similarly, for finite feedback amplitudes, the size of the domain of stability can be estimated. For this purpose, Lyapunov functions as the sum of the translational and rotational kinetic energies of both the passive and active tissues and the gravitational energy are considered. The system is stable when the loss of potential energy due to the motion of the system is more than compensated by the energy stored in the elastic structure of the system and sufficient loss occurs in the system.
3. Ballistic Movement
Point-to-point movements can be slow or fast. Slow movements, where the trajectory of motion is defined by linear segments between the initial and final positions, have been considered before [115] . Relatively fast move- ments are discussed in [1] [116] . Hannford and Stark [117] have discussed three actuation phases for such movement. In the beginning phase, initial velocities launch the system. In the middle phase, the system coasts. In the final phase, the movement is quickly brought to a halt. The three phases [118] . are considered below.
3.1. Initial Phase of Acceleration
Suppose the initial stationary position of the arm is specified by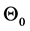 . Let the initial desired angular velocity be
. Let the initial desired angular velocity be 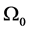 [119] . Suppose the input is a nine-vector of impulsive moment of forces with magnitude
[119] . Suppose the input is a nine-vector of impulsive moment of forces with magnitude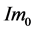 . From Equa- tion (3), it follows that
. From Equa- tion (3), it follows that
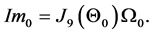
For the three sagittal angular velocities
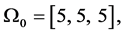
the computed vector of impulses is
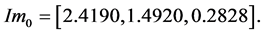
The individual positive impulses correspond to an active agonist. The negative impulses correspond to anta- gonist activity. Zero impulse corresponds to zero activity in the first phase. Other more accurate pulses could be selected based on Fourier studies of the EMG signals [119] . Realistic Hill effect damping is modeled in the muscle dynamics and provides negative intrinsic velocity feedback in the system. The gain of this feedback is assumed constant, but it could be varied and differently programmed.
The implementation of this phase by a central controller is conducted by either of two approaches:
・ By providing ramp type angular inputs during interval T and maintaining the stiffness of all muscles constant, or
・ By programming a linearly rising stiffness during interval T.
These impulses as torques are produced by constant stiffness. Therefore, the angular inputs are impulses. The position angular impulses can be implemented in three ways: by setting initial velocities as a theoretical refer- ence frame, by implementing the impulse as a finite square pulse over a finite period of time T or by triangular pulses over the same interval. The triangular pulse starts with a finite slope and abruptly drops to zero at time T. For a unit impulse, the area of the pulse is unity and, consequently, the slope is![]() . The choice of the pulse is consistent with Kornhuber’s results [51] [58] that the CNS signals are ramp-like. The time interval T is a parameter and can be adjusted to arrive at physically acceptable muscular forces and joint moments of force ( [1] , Table 11.1, page 188).
. The choice of the pulse is consistent with Kornhuber’s results [51] [58] that the CNS signals are ramp-like. The time interval T is a parameter and can be adjusted to arrive at physically acceptable muscular forces and joint moments of force ( [1] , Table 11.1, page 188).
3.2. The Coasting Phase
The second phase of the fast movement is coasting, where both the agonists and the antagonists are turned off. There are no angular inputs to the system in this phase, but, for stability purposes, precise velocity feedback is necessary to prevent tremors and oscillations. The linear velocity feedback is implemented by a spinal reflex loop where afferent spindle signals are involved [62] [63] [80] . There is a finite neural transmission delay here. The CNS, through spinal control signals, must precisely regulate the minimal velocity feedback for stability purposes. This velocity feedback cannot depend on the general friction losses in the system and, depending on the characteristics of the desired movement, is learned and regulated by cerebellar control.
3.3. The Stopping Phase
The stopping phase is characterized by centrally defined and programmed input angles. These angles define the terminal position. Co-activation of agonist and antagonist muscles implement the necessary position feedback. The needed precise velocity feedbacks are implemented by spindle feedback and spinal reflexes. The latter velocity feedback loops also involve afferent and efferent transmission delays.
The strategy articulated above is consistent with some of the later studies of slow and ballistic movements [2] . It is worth repeating that in the present formulation, co-contraction takes place only in the stopping phase of movement. At the same time, the issues of the involvement of the motor cortex and motor memory in execution of ballistic movements constitute challenging research problems for the future [120] and ( [55] , pages 440-441). An alternative movement to consider would be the underhand fast pitch in softball, where two phases of accele- ration and stopping may suffice.
4. Timing and Neural Implementation
Three timing issues involved in the movement are presented here and the possible neural involvement of the hippocampus, the reticular formation, the basal ganglia and the cerebellum are delineated. The three timing issues are:
・ reversal of motion timing,
・ parallel event timing, and
・ serial event timing.
For ease of presentation and communication, the functions are illustrated with simple daily events.
4.1. Reversal in Time
The hippocampus is reported to be involved in reversal of motion in animals. Running a movie projector back- ward produces a reversed motion in time. For translational reverse motion (locomotion) in humans or animals, the trajectories of one point should be stored and then reproduced backwards. More importantly, the central control sequences also have to be executed to fit the reverse translational movement.
The point of reference for this purpose is the human head, where the vestibular otolith organs measure the linear acceleration of the head. The hippocampal neural network for reversing the trajectories and the control of movement is shown in Figure 1. Vision and other sensory inputs or external cues are ignored in this paper. The vestibular linear acceleration signals from the otolith must be integrated twice to produce the trajectories of the translational motion. These position trajectories are stored in memory structures that are capable of reflecting the trajectories in time. These memory and processing structures are analogous to putting an ordered sequence of objects in a basket (what goes in last comes out first.) The needed control sequences for the reverse motion are more complicated and do not necessarily correspond to the reverse of the stored control signals.
The memory structure, mentioned above, may be involved in parallel timing and conditional reflexes, where internal events may have to be timed and synchronized with external events, as is discussed below. These
![]()
Figure 1. Hippocampal processing for motion reversal. The signals are: S1: otolith linear accelerations, S2: translational velocities, S3: position trajectories, and S4: generated backward trajectories. The processors are I1: time integrator, P1: LIFO processing, and P2: control processing. The commands are C1: to initiate reverse motion, and C4: to output reverse motion.
memory structures also have applications in computer design and programming, and are subsumed under the name Last-In-First-Out (LIFO) stacks. One major use of LIFOs is in multi-level interrupt implementation where, under a higher priority interrupting task, all the registers (states) of the computer are pushed into a stack and wait to be popped after the higher priority task is completed. Human CNS interrupt systems have not been studied in detail at this time. In current computer design all such processing is discrete and an external synchro- nous clock orchestrates all events and steps (stack processing).
An analog version of the implementation of the needed memory structure may take place in the reticular formation where “transmission delay lines” store the trajectories as they flow from the cortex outwards. Upon command C1, they transfer all the information in parallel to an inward-flowing transmission delay line that reverses the trajectory. This process can be imagined as a reflection of the time trajectory about a vertical time line at the moment for reversal. Delay line information and storage also can model procedural memory or short- term memory. Capacity and information loss are two characteristic attributes. The implementation is by neural networks [121] . Newer information will push out older information and short-term memory experiences loss of information over time.
A variation of reverse motion is in periodic movements [122] and dance, where the reverse trajectory may not necessarily be a reflection of the forward trajectory [37] [66] . In this case, an internal clock or the extracted beat of the music (period of beat = T) sets up a clock with period T. The period of the periodic dance motion will be a fixed integer multiple of T. The clock cycle T is used in the basal ganglia for construction of “ramp-like” segments of the motion in successive T intervals [60] . The neural element for one such trajectory construction is sketched later in the paper. The periodic trajectory construction by the basal ganglia is shown in Figure 2.
4.2. Parallel Timing
The classical conditioning experiment [73] is discussed first. Only amplitude modulation is envisioned. The conditioning is represented as a 10-state discrete time event as described below.
・ State 0: The unconditioned stimulus ![]() begins and the system starts to measure the duration of the stimulus
begins and the system starts to measure the duration of the stimulus![]() .
.
・ State 1: Puff of air is detected![]() , ending the measurement and holding or storing
, ending the measurement and holding or storing![]() .
.
・ State 2: Initiate closure of eyes ![]() and measure duration of it
and measure duration of it![]() .
.
・ State 3: Eyes are closed. Hold or store![]() .
.
・ State 4: Do subtraction:
![]() .
.
・ State 5: Wait for next![]() .
.
・ State 6: ![]() arrives and its duration is measured in
arrives and its duration is measured in![]() .
.
・ State 7: Set ![]() equal to
equal to![]() .
.
・ State 8: Initiate CS (closing of eyes).
・ State 9: Eyes are closed, Repeat the above 10-state cycle if necessary.
The discrete event system is shown in Figure 3.
Alternatively, suppose two internal events of different duration must end simultaneously (for example, due to different efferent delays in the execution path.) Suppose the time durations of the two signals are known. One
![]()
Figure 2. The design of periodic movements in the basal ganglia based on time intervals T. Alternatively, the trajectories could be recalled from storage in the cortex, but may have to be rescaled in time to fit the extracted beat.
![]()
Figure 3. The 10-state representation of a discrete time event for classical conditioning.
delays the faster event so that the terminal time of the two events coincide [102] [123] . Let both events be stored in tapped delay lines. One physiological analog is the parallel fibers in the internal cerebellum processing. A second example is the processing in the reticular formation. A more general case is the terminal synchronization of an arbitrary number of signals. The pairwise computations may not be efficient or quick enough for the CNS. An example of such large events is fixed action patterns ( [72] , Fig. 63.3). It is stated on page 989 that, “each species has a repertory of fixed action patterns generated by central programs.” Presumably, the shaping and timing of these patterns are learned. We only consider the timing issues here.
Two alternative neural structures for this purpose are stacks where concepts from clocked array processing are useful and internal cerebellum-like parallel structures and processing. Let there be n existing events, all having a starting point in time and a stopping point. The beginning point ![]() and end point
and end point ![]() of each event is well marked and known and
of each event is well marked and known and
![]()
Let there be n LIFO stacks, the depth of all being longer than the longest of the n time events. The functioning here is formulated as a clocked discrete time system [84] . Let the depth of the stack be d. The state ![]() is of dimension
is of dimension ![]() at time k. Let the event vector X be of dimension n. The control signals are pop, push, and inhibit. The push and pop operations are the standard. The inhibition’s operation is more complex and state- dependent and is discussed in some detail below.
at time k. Let the event vector X be of dimension n. The control signals are pop, push, and inhibit. The push and pop operations are the standard. The inhibition’s operation is more complex and state- dependent and is discussed in some detail below.
The state-space behavior of this linear system is described in words below and can be formulated in matrices:
・ If push and pop are both off, do nothing. The state remains as it was.
・ When push is on, the n values of the events are pushed onto the stack. This operation is continued until the longest event is stored.
・ After the longest event is stored, the pop signal comes on.
・ When pop is on, the immediate values of the top of the stack are extracted.
・ When ![]() is to be popped, the inhibition signal i becomes active and discourages any further popping on stack i.
is to be popped, the inhibition signal i becomes active and discourages any further popping on stack i.
So, the procedure of the stack system pushes all signals in and pops each until ![]() reaches the top of the stack. Therefore, once popping is stopped, all the events are synchronized with their last value on the top of the stack. With a second simple stack operation, all the signals, except the longest, are recovered with arbitrary delays in the beginning of each, so they are all synchronized at the end.
reaches the top of the stack. Therefore, once popping is stopped, all the events are synchronized with their last value on the top of the stack. With a second simple stack operation, all the signals, except the longest, are recovered with arbitrary delays in the beginning of each, so they are all synchronized at the end.
It is assumed here that all signals are amplitude modulated, are properly scaled and no time expansion or contraction is necessary. The only operation is that all signals are delayed such that the end of execution is the same for all of them. It is also assumed that the cerebellar parallel fibers are regularly tapped with control inputs and their values output at all the ![]() array. Each node also has a second output that identifies whether the node is the beginning or the end has the signal. Suppose the array is
array. Each node also has a second output that identifies whether the node is the beginning or the end has the signal. Suppose the array is![]() . Suppose the signals are all entered from the right so that all end markers are on the right side and all the beginning markers are on the left. The operation of synchronization starts with the following sequence of operations:
. Suppose the signals are all entered from the right so that all end markers are on the right side and all the beginning markers are on the left. The operation of synchronization starts with the following sequence of operations:
・ Step 1: Detect or identify the left-most marker (i.e., identification of the longest signal, say signal J). This operation is simplified by projecting all the n end signals on a parallel fiber that is not a data delay line, but a control delay line.
・ Step 2: Produce an output signal from the detector that inhibits channel j from any inputs but allows all the other channels to accept a zero signal as input.
・ Step 3: Repeat Step 2 above until a second channel’s end signal, say channel k overlaps![]() . Now channel k is also inhibited from taking any more zero inputs. Also, channel 2 is now synchronized with channel j;
. Now channel k is also inhibited from taking any more zero inputs. Also, channel 2 is now synchronized with channel j;
・ Step 4: Repeat step 2, except now both channels are inhibited from accepting inputs.
・ Step 5: Repeat inserting zeros until another channel is synchronized.
・ Step 6: Stop when the last channel is synchronized, and
・ Step 7: Empty the parallel fiber array from the left to some appropriate memory.
4.3. Sequential Timing
For the ballistic movement here, the control must be designed differently for three consecutive intervals of time of known durations. The production of these signals, produced in the basal ganglia and issued to the cerebellum in “climbing fibers”, is shown in Figure 4 where the input signal is unity. The output is proportional to time. Once the first interval is constructed, the circuit starts the second interval, and so forth. Sequential triggering of signals and chaining is one way to generate commands for complex movements. The same neural circuit could be used to measure duration of CS in the conditional reflex measurement. Another variation of this basal ganglia circuit is used for pattern generation [60] . The circuit demonstrates the flexibility of the CNS in using the same circuits with synaptic and interneuron control for a variety of goals and purposes ( [71] , Chapter 65). The process of measuring time durations in the basal ganglia can be compared with the stack-processing method of per- forming the same computations. Stack processing is much simpler, but not as versatile. It can be conjectured that perhaps the stack system is the processing unit in nature’s more primitive nervous systems. By changing the
slope of the ramp signal, the duration of any event can be changed. A slope larger than unity produces a com- pressed signal, and a slope less than unity stretches the signal linearly in time.
5. Simulation of Ballistic Movement
The simulation has four components here: the basal ganglia for time and trajectory construction, the cerebellum for setting the gains, the musculoskeletal system and the spinal reflexes. The ramp-type trajectories for time measurement and pattern generation are constructed in the basal ganglia [60] and ( [55] , Table 23.1, page 448). The first phase of movement starts as output of a block. When the first phase is complete, a trigger starts the second phase and, subsequently, a third phase. Asynchronous “one-shot” electronic circuits without a clock could be used to measure the three time intervals.
The cerebellum is involved in the selection of the activation levels of the muscles in phase one, in inhibition of position-dependent forward activation and disinhibition of spinal reflexes in phase two, and in both co- activation and maintenance of precise spinal reflexes in phase three. These inhibitions and disinhibitions occur in the motor cortex for preprogrammed movements according to Evarts ( [65] , page 178), and also conform to the summary of functions of the cerebellar outputs as given by Brooks ( [73] , page 287). Other activities may be involved in this path to the cortex, as discussed by Ghez ( [124] , page 637).
From input position angles ![]() and known gains K, the cerebellum produces products
and known gains K, the cerebellum produces products![]() . In a better model than this, the cerebellum would produce many output
. In a better model than this, the cerebellum would produce many output ![]() functions for a corresponding input
functions for a corresponding input ![]() signal. The following assumptions are made:
signal. The following assumptions are made:
・ The basket, Golgi and stellate cells regulate internal gains and internal stability of the cerebellum.
・ The cerebellum is assumed as a memoryless algebraic function generator, consistent with Pellionisz and Llina’s hypotheses [125] - [127] , where there are outputs from Purkinje cells (or sums of Purkinje cell outputs) and two classes of inputs.
・ Climbing fibers as (possibly binary) discrete events and conditions are one input class.
・ Mossy fiber inputs are trajectories and other functions of time.
・ The possible addition (or summing) of Purkinje cell outputs to construct larger signals (in frequency), which may require delicate timing mechanisms, is also ignored. Simple amplitude addition is employed here.
The requirement that all the signal processing in the cerebellum be formulated in frequency domain and with pulse signals merits a challenging and independent study. It also requires that the Purkinje cell outputs involved for the same large ![]() function have differently timed windows such that their pulses add together in adjacent intervals of time. This mechanism allows construction of signals with large intensity. It could also explain the “inhibitory” nature of the Purkinje cells.
function have differently timed windows such that their pulses add together in adjacent intervals of time. This mechanism allows construction of signals with large intensity. It could also explain the “inhibitory” nature of the Purkinje cells.
A sketch of the control activity of the three phases is shown in Figure 5.
We also note that reversing the control here does not reverse the movement. The movement is from a vertically extended position and takes place in the sagittal plane. Initially, all 18 positions and velocities are zero.
![]()
Figure 5. A block diagram sketching the control machinery involved in the neural control. All three phases have inputs constructed in the basal ganglia-ramp signals for the first phase and constant signals for phases two and three. The inhibitory and disinhibitory activation signals are issued by the cerebellum-inhibiting antagonists in phase one, inhibiting both agonists and antagonists in phase two, and dis-inhibiting both groups in phase three. The rest of the arm muscles and the torso are co-activated to maintain a steady arm and a stationary torso.
In the terminal state, the three sagittal (pitch) angles are, respectively, ![]() radians and the rest of the position states (roll and yaw angles) and all the velocities are zero. The stiffness matrix is constructed from nine pairs of single-joint and six pairs of biarticular muscles, and is assumed to be constant throughout the movement. It is given in the Appendix.
radians and the rest of the position states (roll and yaw angles) and all the velocities are zero. The stiffness matrix is constructed from nine pairs of single-joint and six pairs of biarticular muscles, and is assumed to be constant throughout the movement. It is given in the Appendix.
The initial phase is assumed to take 10 ms and the three sagittal angles, i.e., the three pitch angles of the upper arm, lower arm and hand are expected to rise to 5 rad./sec. The triangular pulse scheme is used for 10 ms to initiate the movement. The three angles, angular velocities and the negative feedback moments of forces at the joints are shown in Figure 6. The other six angles remain zero and are not plotted. If the rest of the body, i.e., the torso, etc. was modeled (under co-activation) it would provide a stable platform as an inertial coordinate system from which the arm’s movement is launched.
At t = 0.5 second, i.e, the end of the free coasting cycle, the three nonzero sagittal positions are
![]()
The three non-zero sagittal velocities are
![]()
As can be seen, only the sagittal pitch position and angles are non-zero. Suppose it is desired to stop the system at that state. For the last phase, co-activation is implemented and, further, spinal reflex feedback is used to slow the system to an over-damped halt with no terminal oscillations. The gain of the spinal reflex is 0.2 in the coasting phase and unity in the stopping phase. This means about one fifth of co-activation gains in coasting and unity in the stopping phase. The co-activation gains are kept constant in the simulation of the ballistic movement. The three angles, angular velocities, and the negative feedback moments of forces at the joints are shown in Figure 7.
![]()
Figure 6. The agonist impulsive phase 1 of the movement: the three pitch angles, angular velocities and joint damping due to Hill effect are shown as functions of time.
![]()
Figure 7. The whole ballistic movement: the three pitch angles, angular velocities and joint damping due to spinal reflexes (active in phases two and three) are shown as functions of time. No delay is included in the reflex paths.
In the next three simulations, neural transmission delays are added to the spinal reflex. In Figure 8, a delay of 5 ms is added in the neural path of the spinal reflex.
In Figure 9, the delay is increased to 10 ms. In Figure 10, the delay is kept at 10 ms, but the gain of the spinal reflex feedback loop is reduced by half for all three muscles involved.
6. Discussion and Conclusions
Neural modules were presented for the implementation of ballistic movements that may be reversed in time or conditioned and synchronized with external events. The role in the execution of movement of four central neural structures, hippocampus, the reticular formation, the basal ganglia and the cerebellum, was outlined.
The role of procedural memory was illustrated. Time scaling by basal ganglia circuits was demonstrated. Neural structures involved in time reversal of trajectories were discussed. Reversal of control sequences was not considered and remained a challenge for the future. Use of LIFO stacks for synchronization of large numbers of signals was formulated.
The point-to-point fast movement is implemented by assuming that the CNS has information about the nine Bryant angles at the initial and terminal position of the arm. Such information could be inferred by the CNS from the stretch responses of all the muscles that are relayed to the CNS at any position of the arm, and then kept, in an associative memory, with the visually encoded position of the arm. More research is necessary to establish the above hypotheses.
The central feed forward signals were the desired limb trajectories. The co-activation of 15 pairs of agonist- antagonist muscles produced the necessary muscular feedback. The tendons played a role here in controlling of their length allow control of stiffness.
![]()
Figure 8. The whole ballistic movement: the three pitch angles, angular velocities and joint damping due to spinal reflexes (active in phases two and three) are shown as functions of time. The delay in the reflex path is 5 ms.
![]()
Figure 9. The whole ballistic movement: the three pitch angles, angular velocities and joint damping due to spinal reflexes (active in phases two and three) are shown as functions of time. The delay in the reflex path is 10 ms. The gain of the reflex feedback loop is the same as the previous case.
![]()
Figure 10. The whole ballistic movement: the three pitch angles, angular velocities and joint damping due to spinal reflexes (active in phases two and three) are shown as functions of time. The neural delay in the reflex path is 10 ms, and the gain of the reflex feedback loop is half as much as for the previous figures.
It is instructive to compare the co-activation strategies of this paper with the ones attributed to the human system ( [73] , Fig. 4.11). The model here has to be contrasted with “length follow-up servo” as in ( [73] , Fig 4.11 A and B).
The gains of the feed forward path are set centrally, and not mediated by Golgi and ![]() afferent signals involved in feedback from the spinal cord ( [73] , Fig 4.11 C). Finally, precisely controlled spinal reflexes of velocity are needed in the third phase of the ballistic movement. The ballistic movement was specified and controlled in three phases of initial acceleration, coasting, and stopping. All three phases require construction of reference input trajectories in the basal ganglia and inhibition and disinhibition of muscular activities, prompted by the CNS and spinal reflexes by the cerebellum. Computer simulation showed how the system works, and the effect of delays in the spinal reflex loop was demonstrated.
afferent signals involved in feedback from the spinal cord ( [73] , Fig 4.11 C). Finally, precisely controlled spinal reflexes of velocity are needed in the third phase of the ballistic movement. The ballistic movement was specified and controlled in three phases of initial acceleration, coasting, and stopping. All three phases require construction of reference input trajectories in the basal ganglia and inhibition and disinhibition of muscular activities, prompted by the CNS and spinal reflexes by the cerebellum. Computer simulation showed how the system works, and the effect of delays in the spinal reflex loop was demonstrated.
Existing measurements could be used to tune the model parameters and improve the model and the simulation results. With recent posture estimation techniques [128] [129] , one could train or teach robots to play softball [130] . The performance of the above model can be improved [131] for human applications [132] - [134] and by anatomical accuracy [45] - [47] . More quantitative studies of the sensory and processing deficits, injuries and deficiencies could be undertaken [104] [106] [132] .
Acknowledgements
The authors are very grateful and indebted to Professor H. C. Ko, former chair and professor emeritus of the Electrical and Computer Engineering Department at The Ohio State University, for his generosity, vision, sustained support and encouragement of this work. We would like to acknowledge support of R. J. Garbacz, Lee Potter, Patrick Roblin and Vadim Utkin. We are indebted to Darla Peelle and David B. Ball for editorial assistance and inspiration.
Appendix
A.1. Physical Parameters
The physical parameters used in the computer simulations are given in the table below.
A.2. Gains
The gain matrix for the simulations is given in table below. The linear viscosity, in the first phase, is assumed to be 1/8 of the stiffness for all actuators.
![]()