Subject Areas: Applied Physics
1. Introduction
Von Neumann introduces the Hilbert space and he tries to present axioms of quantum mechanics [1] . He introduces projective measurement theory. For example, the values of the result of quantum measurements are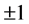 
(in 
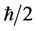unit) in spin-1/2 system. An important note here, von Neumann’s theory does not say that we can measure non-commuting observables, simultaneously. Therefore, each value of measurement depends time even though we do not indicate any suffix concerning time. The detail argument can be seen in Ref. [2] where we indicate a suffix concerning time. von Neumann’s theory is necessary to perform quantum computer. It is said that there is not any quantum computer without von Neumann’s theory.
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from digital computers based on transistors. Whereas digital computers require data to be encoded into binary digits (bits), quantum computation utilizes quantum properties to represent data and perform operations on these data [3] . A theoretical model is the quantum Turing machine, also known as the universal quantum computer. Quantum computers share theoretical similarities with non-deterministic and probabilistic computers, like the ability to be in more than one state simultaneously. The field of quantum computing was first introduced by Richard Feynman in 1982 [4] [5] .
Here we review to discuss that there is a crucial contradiction within von Neumann’s formalism of the quantum theory [2] [6] [7] . Especially, we reexamine the quantum-theoretical formulation of Deutsch’s algorithm [8] as the earliest quantum computer. We result in the fact that the formulation is questionable despite the fact that we indeed have raw experimental data. We systematically describe our assertion based on more mathe- matical analysis using raw data. This point gives us new important insight rather than the argumentations presented in Refs. [2] [6] [7] .
We review the contradiction as follows. We derive a proposition concerning a quantum expected value under the assumption of the existence of the directions in a spin-1/2 system. The quantum predictions within the formalism of von Neumann’s projective measurement (the results of measurements are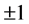
) cannot coexist with the proposition concerning the existence of the directions. Therefore, there is a crucial contradiction in the set of propositions of von Neumann’s theory in a spin-1/2 system.
2. There Is a Contradiction within Von Neumann’s Theory
First, we review that there is a contradiction within von Neumann’s theory along with the argumentation of Ref. [7] .
Assume a pure spin-1/2 state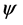 
lying in the x-y plane. Let 
be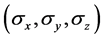
, the vector of Pauli ope- rators. The measurements (observables) on a spin-1/2 state lying in the x-y plane of 
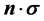are parameterized by a unit vector 
(its direction along which the spin component is measured). Here, 
is the scalar product in
.
We have a quantum expected value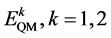 
as
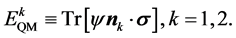(1)
We have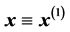
, 
, and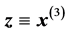 
which are the Cartesian axes relative to which spherical angles are measured. Let us write the two unit vectors in the plane defined by 
and 
in the following way:
![]()
(2)
Here, the angle ![]()
takes only two values:![]()
.
We derive a necessary condition for the quantum expected value for the system in a pure spin-1/2 state lying
in the x-y plane given in (1). We derive the possible values of the product![]()
. ![]()
is
the quantum expected value given in (1). We see that![]()
. We use decomposition (2). We
introduce simplified notations as ![]()
and ![]()
Then, we have
![]()
(3)
where we use the orthogonality relation![]()
. From a proposition of the quantum theory, the Bloch
sphere (the directions) with the value of ![]()
is bounded as![]()
. The reason of the condition (3) is
the Bloch sphere ![]()
Thus we derive a proposition concerning a quantum expected
value under the assumption of the existence of the directions (in a spin-1/2 system), that is,![]()
. It is worth noting here that this inequality must be saturated if ![]()
is a pure state lying in the x-y plane. That is,
![]()
Hence we derive the following proposition concerning the existence of the directions
when the system is in a pure state lying in the x-y plane
![]()
(4)
![]()
is the maximal possible value of the scalar product.
On the other hand, let us assume von Neumann’s projective measurement. In this case, the quantum mean value, which is the average of the results of projective measurements, is given by
![]()
(5)
We can assume as follows by Strong Law of Large Numbers,
![]()
(6)
where ![]()
is given in (1). The possible values of the actually measured result ![]()
are ![]()
(in ![]()
unit). Same quantum mean value is given by
![]()
(7)
where![]()
. We only change the labels as ![]()
and![]()
. Of course, the possible values of the actually measured result ![]()
are ![]()
(in ![]()
unit). Thus, we have
![]()
(8)
And
![]()
(9)
By using these facts, we derive a necessary condition for the quantum mean value for the system in a pure spin-1/2 state lying in the x-y plane given in (5). The quantum mean value ![]()
is given in (5). We have
![]()
(10)
Clearly, the above inequality can be saturated since, as we have said,
![]()
(11)
and
![]()
(12)
We derive the possible values of the product![]()
. Thus we derive a
proposition concerning a quantum mean value under the assumption that von Neumann’s projective mea-
surement is true (in a spin-1/2 system), that is,![]()
. This is true when![]()
. From Strong Law
of Large Numbers, we have
![]()
(13)
Thus, we have
![]()
(14)
Hence we derive the following proposition concerning von Neumann’s projective measurement
![]()
(15)
Clearly, we cannot assign the truth value “1” for two propositions (4) (concerning the existence of the directions) and (15) (concerning von Neumann’s projective measurement), simultaneously, when the system is in a pure state lying in the x-y plane. Therefore, we are in the contradiction when the system is in a pure state lying in the x-y plane.
3. Deutsch’s Algorithm
Next, we review Deutsch’s algorithm along with Ref. [9] .
Quantum parallelism is a fundamental feature of many quantum algorithms. It allows quantum computers to evaluate the values of a function ![]()
for many different values of x simultaneously. Suppose ![]()
is a function with a one-bit domain and range. A convenient way of computing this function on a quantum computer is to consider a two-qubit quantum computer which starts in the state![]()
. With an appropriate sequence of logic gates it is possible to transform this state into![]()
, where ![]()
indicates addition
modulo 2. We give the transformation defined by the map ![]()
a name,![]()
.
Deutsch’s algorithm combines quantum parallelism with a property of quantum mechanics known as interference. Let us use the Hadamard gate to prepare the first qubit ![]()
as the superposition![]()
, but let us prepare the second qubit as the superposition![]()
, using the Hadamard gate applied to the
state![]()
. The Hadamard gate is as ![]()
Let us follow the states along to
see what happens in this circuit. The input state
![]()
(16)
is sent through two Hadamard gates to give
![]()
(17)
A little thought shows that if we apply ![]()
to the state ![]()
then we obtain the state ![]()
. Applying ![]()
to ![]()
therefore leaves us with one of two possibilities:
![]()
(18)
The final Hadamard gate on the first qubit thus gives us
![]()
(19)
Realizing that ![]()
is 0 if ![]()
and 1 otherwise, we can rewrite this result concisely as
![]()
(20)
So by measuring the first qubit we may determine![]()
. This is very interesting indeed: the quantum circuit has given us the ability to determine a global property of![]()
, namely![]()
, using only one evaluation of![]()
! This is faster than is possible with a classical apparatus, which would require at least two evaluations.
4. A Problem of Deutsch’s Algorithm
In what follows, we discuss a problem of Deutsch’s algorithm. We see that the implementation of Deutsch’s algorithm is not possible if we give up either observability of a quantum state or controllability of a quantum state.
We introduce the following quantum proposition concerning controllability:
![]()
(21)
We may consider the following non-quantum-theoretical proposition:
![]()
(22)
The proposition (22) implies the validity of von Neumann’s projective measurement (observability). The proposition (22) implies
![]()
(23)
However, the validity of von Neumann’s projective measurement does not imply the proposition (22). We see that the proposition (21) is not equivalent to von Neumann’s projective measurement (observability). We see that we can assign the truth value “1” for von Neumann’s projective measurement (observability) and we can assign the truth value “0” for the proposition (21) concerning controllability.
The proposition (21) implies that ![]()
when the system is in a pure state lying in
the x-y plane. The reason is as follows: Assume a pure state lying in the x-y plane as ![]()
where
![]()
is a phase. Let us write ![]()
and![]()
. Then we have ![]()
and![]()
. Therefore, we see![]()
. We thus see the
proposition (21) implies that there are directions in the Hilbert space formalism of the quantum theory.
From the discussion presented in the previous, we see that the quantum proposition (21) concerning con- trollability (the directions) cannot coexist with the validity of von Neumann’s projective measurement (obser-
vability), which states![]()
, when the system is in a pure state lying in the x-y plane.
Deutsch’s algorithm shows the importance of the ability of the Hadamard gate (controllability and the existence of the directions) for quantum computation. The ability of the Hadamard gate is valid only when we assign the truth value “1” for the proposition (21) (the directions). We see that the quantum state ![]()
is a pure state lying in the x-y plane. We can assign the truth value “1” for the ability of the Hadamard gate (controllability and the existence of the directions)
![]()
(24)
only when we assign the truth value “1” for the proposition (21) concerning controllability (directions) and we give up the validity of von Neumann’s projective measurement (observability). The validity of the proposition (21) implies that![]()
. Thus applying H twice to a state does nothing to it if we accept the proposition (19). When we accept the proposition (21), we have
![]()
(25)
We conclude that the step in which transforms the state ![]()
into the state![]()
, namely the step saying from (16) to (17) is possible only when we assign the truth value “1” for the proposition (21) (concerning controllability and the existence of the directions) and we give up the validity of von Neumann’s projective measurement (observability). The step saying from (18) to (19) is also so. Therefore we question what makes observability if we accept the ability of the Hadamard gate (controllability and the directions). We also question what makes controllability if we accept the validity of von Neumann's projective measurement (observability).
5. Conclusions
In conclusion, we have reviewed that there is a crucial contradiction within von Neumann’s theory. We have reexamined the quantum-theoretical formulation of Deutsch’s algorithm as the earliest quantum computer. We have resulted in the fact that the formulation has been questionable despite the fact that we have indeed had raw experimental data. We have questioned what makes observability if we accept the ability of the Hadamard gate (controllability and the directions). We have questioned what makes controllability if we accept the validity of von Neumann’s projective measurement (observability). Especially, we have systematically described our asser- tion based on more mathematical analysis using raw data. This point improves previously published argumen- tations very much.
What are new physical theories? We cannot answer it at this stage. However, we expect that our discussion in this thesis could contribute to creating new physical theories in order to explain the handing of raw experimental data, to create new information science, and to predict new unknown physical phenomena efficiently.