Subject Areas: Classical Physics, Functional Analysis, Quantum Mechanics

1. Introduction
The debates about the interconnection between the hidden laws of nature and our ability to extract the information necessary to formulate them have perhaps a history as long as study of physics itself. The content of our paper is not related to the philosophical or metaphysical aspects of those discussions. Instead, we choose certain point of view without intention to defend it or to convince the reader that it is the only possible approach. We simply present how the process of knowledge acquisition is realized within that approach. We explore the analogy with the structure of field theories (classical electrodynamics, general relativity and non-relativistic quantum mechanics) and make distinction between the unobservable kinematical quantities which characterize the physical system and the measurable variables which define its dynamics. Since the main distinction between the classical and the quantum physics is in presence of new kinematical quantities―phases, one should learn how to measure the corresponding phase differences. We demonstrate that the required measurement may be performed using special experimental arrangement which we call the quantum reference frames. The use of these reference frames allows communicating the hidden unobservable information into the instruments of the observer. Simultaneously it explains why the elementary unit of the communication is given in terms of indivisible bit.
In order to achieve our goal we establish for classical mechanics the structural framework similar to the one used in quantum theory. We restrict ourselves to description of single particle states and prefer here to avoid complications introduced by special relativity. In order to make clear the mathematical and correspondent physical content for successive discussion, I will quote the following statement [1] :
If 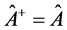 and
and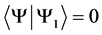 , we can always decompose
, we can always decompose
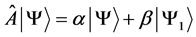
with 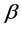 real and non-negative.
real and non-negative.
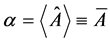
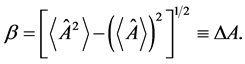
This theorem appears several times [2] in different contexts, but in form presented, its content takes a clear view of the situation: it is enough that wave function of the system will contain two linearly independent (orthogonal) components in order that the correspondent observable will have non-zero dispersion. The non-zero dispersion leads to practically instant spread of wave packet.
Now, let us consider famous E. Schrödinger cat example [3] . The essential assumptions are:
1) The cat may be presented as a quantum mechanical system and not as a classical measurement instrument;
2) The system state is described by the following linear superposition of pure states:
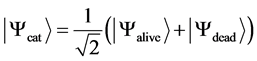 .
.
E. Schrödinger did not continue discussion after that point. But since a cat is in the superposition state, this will lead to the spread of wave packet within time uncertainty predicted by W. Heisenberg. The curious experimenter would find cat “blurred” over entire volume of the chamber and disappeared (from classical point of view) together with his smile (notice that if it was correct, then the quantum mechanics would provide proper unification between L. Carroll and E. Schrödinger fantasies). It was remarkable that E. Schrödinger concluded discussion of cat paradox by the following statement:
“It is typical of these cases that an indeterminacy originally restricted to the atomic domain becomes transformed into macroscopic indeterminacy, which can then be resolved by direct observation”.
That statement is in contradiction with the J. von Neumann conjecture [2] that the macroscopic physics is dispersion free.
2. Real Hilbert Space Formulation of Classical Mechanics
First of all it should be defined what we mean by real Hilbert space. We should maintain the connection with quantum theory as close as possible and assure the proper extension to relativistic version.
In addition, a scheme should incorporate classical electrodynamics through application of principle of local gauge invariance. Therefore we will use the following definitions:
(*)Scalar product in this framework is defined by:

with underlined numerical basis of dimension two (complex numbers). This implies that
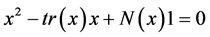 ,
, 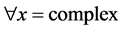 ,
, 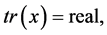
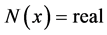 ,
, 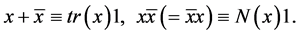
In particular,
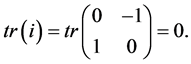
Notice that in quantum theory the relevant scalar products associated with observable quantities are always real. Since in classical mechanics every dynamical variable is observable, we will further discuss only self-adjoint operators. They satisfy the following algebra:
1)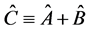 ,
, ![]()
![]()
![]()
This statement will be justified after introduction of a product of two self-adjoint operators.
2)![]() ,
, ![]()
![]()
![]()
Proof:
![]()
![]()
Obviously,![]() .
.
Then
![]()
![]()
Therefore
![]()
with respect to real scalar product defined above.
Since the product of any pair of self-adjoint operators is a self-adjoint operator, the product of an arbitrary number of self-adjoint operators is a self-adjoint operator.
Now let us examine properties of self-adjoint operators in these schemes.
1) Spectral Decomposition Theorem: For every self-adjoint (hermitian) operator ![]() that is suitable for description of the observable dynamical variable (has all necessary properties required by functional analysis), there exists the complete orthonormal basis in Hilbert space uniquely defined by the requirement
that is suitable for description of the observable dynamical variable (has all necessary properties required by functional analysis), there exists the complete orthonormal basis in Hilbert space uniquely defined by the requirement
![]() (1)
(1)
The components of this basis are the solutions of the equation
![]() (2)
(2)
which is a consequence of Equation (1). ![]() are called eigenfunctions of the operator
are called eigenfunctions of the operator![]() . Sets of real numbers
. Sets of real numbers ![]() are called eigenvalues of the operator
are called eigenvalues of the operator![]() , are defined simultaneously with
, are defined simultaneously with ![]() and form a spectrum of
and form a spectrum of![]() . The spectrum of hermitian operator may contain several discrete numbers, a countable set of discrete numbers or/and continuous interval (finite or infinite).
. The spectrum of hermitian operator may contain several discrete numbers, a countable set of discrete numbers or/and continuous interval (finite or infinite).
The careful reader may verify line by line that there is no difference between complex and real Hilbert spaces as defined above with respect to spectral decomposition theorem. There exists vast literature on the topic but the books of R. Courant and D. Hilbert [4] and J. von Neumann [2] still remain useful.
Here perhaps I should add the important remark. When we write
![]()
we usually say that it provides physical value(s) of the observable![]() . It does not. Wave function
. It does not. Wave function ![]() is not an observable quantity. Wave function
is not an observable quantity. Wave function ![]() is also an unobservable quantity. The value of an observable should be a real number. Only the expression
is also an unobservable quantity. The value of an observable should be a real number. Only the expression
![]()
provides the values of the observable in quantum theory. Therefore, an additional relation is required in order to associate them with the results of measurements.
2) The necessary and sufficient condition for two or any number of hermitian operators to have a common set of eigenfuctions which form a complete orthonormal basis in Hilbert space is that they are mutually commuted. Since the product of two or any number of mutually commuting hermitian operators is again a hermitian operator (and commutes with each of its components), it has the same set of eigenfunctions. Indeed, every one of them in that basis is dispersion free.
Hence, the real Hilbert space as defined above provides realization of dispersion free physical theory.
Moreover, since the coordinate ![]() has a purely continuous spectrum, every observable in this theory has a continuous spectrum. An additional feature, which distinguishes it from the complex Hilbert space framework, is uniqueness of its basis. The theory remains linear and does not exclude validity of linear superpositions for the system states; however, only precise values of hermitian operators are measured. That phenomenon is known as collapse of wave function.
has a purely continuous spectrum, every observable in this theory has a continuous spectrum. An additional feature, which distinguishes it from the complex Hilbert space framework, is uniqueness of its basis. The theory remains linear and does not exclude validity of linear superpositions for the system states; however, only precise values of hermitian operators are measured. That phenomenon is known as collapse of wave function.
3) Another mathematical statement that may have interesting physical realization (we will discuss it later) is valid in real Hilbert space: for an arbitrary set of mutually commuting hermitian operators ![]() there exists hermitian operator
there exists hermitian operator ![]() such that each one of
such that each one of ![]() is a function of
is a function of ![]() [5] .
[5] .
Now it become manifestly obvious that real Hilbert space provides a convenient arena for Newtonian mechanics. Finally, let us demonstrate that the equation
![]() (3)
(3)
is equivalent to the Heisenberg quantization condition.
It is well known that the classical equations of motion
![]()
have the following form in terms of hermitian operators [6] :
![]()
if we choose
![]()
and
![]()
then using Equation (3) we obtain
![]()
which are the quantum equations of motion written in the Heisenberg representation.
The Equation (3) is the fundamental relation that defines the results of measurements. For the model example of a particle in an infinite spherical well, only discrete solutions of right hand side embedded into continuous spectrum of left hand side will be revealed.
3. Theory of Measurements
In the previous section the formulation of Newtonian dynamics was achieved and was even demonstrated that the same dynamical law still governs time evolution of the system in quantum physics. It was discovered by E. Schrödinger [7] that the alternative equivalent form of equations of motion exists in non-relativistic version of the theory. However, what is mentioned by the notion “physical law” still remains undefined.
We may say that for the mathematical structure it is sufficient to be legal and legitimate if its foundation is based on mutually consistent set of assumptions. It is not sufficient for physics: physics is an empirical science. The realization of that requirement is performed through introduction of properly defined measurement instruments and procedures. The structure of Newtonian mechanics represents the basic ingredients needed to achieve that. In addition to the formulation of the time evolution of the system (dynamics), the equations of motion should earn status of physical law. The latter requirement is satisfied by introduction of the reference frames and rules as how they are connected with each other. It is meaningless to discuss any law or relation without its universality with respect to a chosen and well defined infinite set of reference frames. In the classical mechanics, it turns out that the definition of the suitable reference frame (inertial systems) occurs through the idealization of the free moving body isolated from its environment. Then the connection between those frames is given in terms of the motion of such a body. This is the content of the first law of the Newtonian mechanics (Galileo law of inertia), which is indeed consistent with the fundamental equations of motion. We associate that body, located at the origin of a given reference frame, with an appropriate set of measurement instruments. Therefore the origin of the reference frame should be defined with certainty and the measurement instruments should obey laws of classical physics.
In the scheme suggested here, both requirements are met and Equation (3) assures that all relevant information about properties of investigated quantum mechanical system is available. Equation (3) plays a role analogous to the third
Newton
law.
A single isolated sample of the experimental data has no meaning in classical physics. Only repetitions of the sample will confirm that the obtained result represents the objective reality. The requirement that the system state remains unchanged during the experiment was never fulfilled; even the system invariants (for example in collisions) may change. What is essential is that if the consecutive (in time) measurements on the same system are not legal, the repetition of the measurement should be assured by possibility to prepare a system identical to the original one. As pointed out by E. Schrödinger [3] the measurements of quantum mechanical systems allow unprecedented precision as well as preparation of the identical experiments (feature inherent to objective property of the quantum systems―the identical particles are undistinguishable; a situation which is not available within the classical world).
The collection of the obtained results is now the subject of the standard techniques for the data processing. In case the system under test is a classically defined material point (coordinate and momentum are mutually commuted hermitian operators), one will obtain a picture sharply concentrated around a single isolated point. In case when the system obeys the laws of quantum physics, one will get a picture of a spatially extended object; the number of required samples is determined by the classical methods of image and/or signal processing [8] . There is no any importance to our subject that the sequence of samplings emerged in random fashion; no doubt that the obtained result reconstructs the objective reality exactly in the same manner as the image of the classical material point was obtained.
4. Eigenschaften Operators
The notion of eigenschaften operator was introduced by J. von Neumann [2] as the necessary ingredient of the theory of measurements. He suggested assigning that role to the projection operators. However, projection operators define the space of quantum mechanical states, they define the structure of that space and its orthonormal and complete basis. It is logically inconsistent to describe the alternatives by the tool that annihilates the alternative possibilities; rather it seems natural to use the operators that keep all possibilities open. Therefore, the eigenschaften operators must be closely related to projection operators but act on whole space without distortion, that is, eigenschaften operators must be unitary.
Together with the requirement of being observable (![]() ) that leads to the following statement:
) that leads to the following statement:
Theorem.
If ![]() (unitary) and
(unitary) and ![]() (self-adjoint),
(self-adjoint),
Then
![]() (4)
(4)
Proof:
1) Suppose
![]()
then
![]()
2) Suppose
![]()
then
![]()
From ![]() we have
we have
![]() (5)
(5)
Let us consider first the two-dimensional case. From the Equation (5)
![]() (6)
(6)
and due to the spectral decomposition theorem, we have
![]() (7)
(7)
Since
![]() (8)
(8)
finally we obtain
![]() (9)
(9)
Now in terms of matrix mechanics we have
![]()
![]() (10)
(10)
with
![]()
![]() (11)
(11)
Then
![]() (12)
(12)
Since here we discuss the measurements of relevant parameters of the quantum mechanical systems with non-vanishing dispersion, we will consider only ![]() case. Then
case. Then
![]() (13)
(13)
or
![]() (14)
(14)
The matrix elements
![]() (15)
(15)
and
![]() (16)
(16)
are all we need to know about the quantum state. Both are measurable, ![]() define the spectrum and
define the spectrum and
![]() define the dispersion. The basis introduced above
define the dispersion. The basis introduced above ![]() and
and ![]() is distinguished by the fact that it allows measurement both of them simultaneously. Perhaps the example of two level systems makes that even more clear:
is distinguished by the fact that it allows measurement both of them simultaneously. Perhaps the example of two level systems makes that even more clear:
![]() (17)
(17)
Then dropping the overall phase factor, we obtain
![]() (18)
(18)
Using the relations (12) we obtain the following most general solution
![]() (19)
(19)
In particular, for ![]() and
and ![]() we obtain the Hadamard matrix of lowest order (N = 2)
we obtain the Hadamard matrix of lowest order (N = 2)
![]() (20)
(20)
well known in image processing applications.
5. Holographic Detection: Quantum Reference Frames
The remarkable feature of the measurement process is that the measurement devices are macroscopic, obeying the laws of classical physics, whereas the systems under test belong to the microscopic world and behave quantum mechanically. Indeed, the measurement setup should assure that the obtained results represent the objective properties of the investigated physical system and not a free subjective imagination of the observer. That task is performed in classical physics by introduction of reference frames such that the detector location defines the frame origin and the set of auxiliary macroscopic devices allows establishing the connection and the communication between the frames separated by the finite space-time interval (the comparison of the obtained empirical data must always be performed by the same observer). Similarly, in order to perform the measurement of the relevant quantum dynamical variable one should include in the classical setup a set of auxiliary macroscopic devices which produce the necessary beam-splitting. Then the required phase differences are measured in the usual way. This setup and recording procedure may be viewed as the general holographic detection. But in contrast to the classical physics, measurements in quantum mechanics should provide simultaneous information about all relevant relative amplitudes (pure states and the transitions between them) and all relevant relative phases. Simultaneity is needed since in general the measurement changes the state of the system (in quantum physics and in classical physics as well). We illustrate that by explicit examples and describe general features of the corresponding experimental setup which we identify as the quantum reference frame.
We address the following questions:
1) What is the difference between “on-off” and “or-and” switches in terms of quantum mechanical self-adjoint operators (observables)?
2) How the transition amplitudes between the stationary (pure) states are incorporated naturally and symmetrically together with the amplitudes of these states?
3) Is it possible to measure ![]() and
and ![]() simultaneously and how to arrange the required setup?
simultaneously and how to arrange the required setup?
4) If it is possible, may that measurement be performed using only macroscopic devices?
It is well known [9] that the product of two noncommuting self-adjoint operators is not a self-adjoint operator and that the dispersion of their product is not a self-adjoint operator also. Therefore, there is no way to assign the physical meaning to its numerical value. The HDR has outstanding theoretical importance telling us that quantum physics is the physics of extended objects and not of the Newtonian material points. The results of measurements are “pictures” and could not be treated as an image of a single space-time point, in principle. The projection operators intensively used by J. von Neumann in formulation theory of measurements obviously play a role of “on-off” switches defining the basis of the state vectors in the Hilbert space. Therefore, it is reasonable to expect that the “or-and” operators should be connected to them but different. The particular example of the suitable candidates is the Hadamard transformations [10] which already find their applications in image process- ing and in the quantum information theory. In addition, the notions of bits and qubits appear naturally as two component wave packets. Finally, in order to provide the laboratory realization of the simultaneous measurement of the relevant amplitudes (relative generalized coordinates) and phase differences one should assure that the wave packet will arrive to each point of the detector screen.
Let us expose the content of our discussion viewed from the eyes of Schrödinger’s cat totally confused by endless debates about his destiny. The usual justification of apparent uncertainty in it refers to HDR. But the empirical evidence clearly tells us that the initial assumption that the cat may be considered as quantum mechanical system containing an inherent indeterminacy which “becomes transformed into macroscopic indeterminacy” [3] is erroneous. If the state of the system (“cat”) is defined, one can measure its dispersion. Now, if in that given state the dispersion is not zero, we deal with an extended object and the expected result of the measurements should be represented by a picture of poor cat “mixed or smeared out in equal parts”; if not, the cat was and will remain in the pure (definite) state, hopefully alive. Now, let us remember what we are doing in the classical case, when only measurements of amplitudes are required. In that case, nobody doubts that the “moon is there” and in addition it is the same for all inertial reference frames, for example (Figure 1) [11] :
The lossless beam splitter here is the macroscopic device which participates actively in the detection procedure (![]() ).
).
In contrast, in microscopic quantum mechanical world (quantum optics) we are required to measure also the phase differences in order to obtain all existent and necessary information about the original object. This may be done using similar setup, for example (Figure 2), but in both cases the mirror and the lossless beam splitter participate in detection only passively; they do not cause the wave function collapse, but allow extracting the phase difference information, since the reference component of the wave packet arrives to each point of the detector screen together with the tested wave packet (within inherent dispersion of the quantum mechanical space-time continuum). Then there is no reason to expect that the obtained picture would not provide the adequate image of the original object.
![]()
Figure 1. Classical optics measurement systems.
![]()
Figure 2. Quantum optics measurement systems.
6. Conclusion
It was demonstrated that non-relativistic classical mechanics might be reformulated in terms of real Hilbert space, with an underlined numerical system of complex numbers. It is worthwhile to mention that similar structures based on real quaternions and real octonions exist. The presence of rich phase structure in the definition of wave functions (system states) should allow the axiomatic introduction of electromagnetic and gravitational interactions by means of application of the principle of the local gauge invariance. The relativistic version of the theory is expected to emerge naturally in suggested frameworks. The present paper is devoted mainly to the problems related to the measurement theory. Within a classical world we are working in Heisenberg representation. Hilbert space appears to be uniquely defined and rigid and plays a role of passive arena for the events associated with the dynamics of the physical system. The space-time continuum plays a similar role in the standard formulation of Newtonian mechanics. It seems reasonable to expect that these arenas are actually identical and the J. von Neumann theorem mentioned above (statement 3) may assign to it the dynamical content.