A Remarkable Chord Iterative Method for Roots of Uncertain Multiplicity ()
Received 23 May 2016; accepted 8 July 2016; published 11 July 2016

1. Introduction
The multiplicity index m of root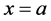 ,
, 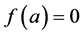 of equilibrium function
of equilibrium function 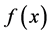 may be a well latent property of the root, not cursorily revealed, nor readily available, yet this multiplicity can profoundly affect the behavior of the iterative approach [1] - [3] to the root. In this note, we briefly review the iterative methods [4] - [8] for approaching a root of an unknown multiplicity, and present a first oder [9] as well as a second order estimate for the multiplicity index m of the approached root. Then we present a novel chord, or a two-step method, not requiring beforehand knowledge of m, nor requiring the higher derivatives of the equilibrium function, which is quadratically convergent for any
may be a well latent property of the root, not cursorily revealed, nor readily available, yet this multiplicity can profoundly affect the behavior of the iterative approach [1] - [3] to the root. In this note, we briefly review the iterative methods [4] - [8] for approaching a root of an unknown multiplicity, and present a first oder [9] as well as a second order estimate for the multiplicity index m of the approached root. Then we present a novel chord, or a two-step method, not requiring beforehand knowledge of m, nor requiring the higher derivatives of the equilibrium function, which is quadratically convergent for any , and then reverts to superlinear.
, and then reverts to superlinear.
2. Assumed Nature of the Equilibrium Function
We assume that near root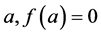 , function
, function  has the power series representation
has the power series representation
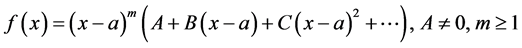 (1)
(1)
where m is the multiplicity index of root a, and where  etc. are, for
etc. are, for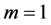 , the coefficients
, the coefficients
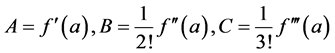 (2)
(2)
and so on.
3. The Newton-Raphson Method
The Newton-Raphson method
 (3)
(3)
is quadratic
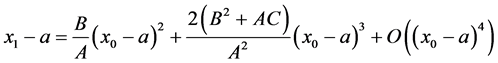 (4)
(4)
if . However, if
. However, if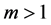 , the method declines to mere linear
, the method declines to mere linear
![]() (5)
(5)
See also [10] .
4. Extrapolation to the Limit
Let ![]() be already near root a. Then, if
be already near root a. Then, if ![]()
![]() (6)
(6)
nearly. Eliminating ![]() from the two equations we obtain
from the two equations we obtain
![]() (7)
(7)
which we solve for an approximate a, as
![]() (8)
(8)
where
![]() (9)
(9)
The square root in Equation (8) may be approximated as
![]() (10)
(10)
and for this extrapolated ![]() of Equation (8) we have
of Equation (8) we have
![]() (11)
(11)
For example, for![]() , and starting with
, and starting with![]() , we compute
, we compute![]() ,
,![]() ; and then from Equation (8),
; and then from Equation (8),![]() . Another such cycle starting with
. Another such cycle starting with ![]() produces a next
produces a next![]() .
.
5. Always Quadratic Newton-Raphson Method
The modified Newton-Raphson method
![]() (12)
(12)
converges quadratically to a root of any multiplicity m
![]() (13)
(13)
But for this we need to know m.
By Equation (1) we readily deduce that, for any x
![]() (14)
(14)
obtained at the price of a second derivative. For finite-difference approximations of the needed derivatives see [11] - [13] . Using ![]() in Equation (14) for m in Equation (12) we obtain the method
in Equation (14) for m in Equation (12) we obtain the method
![]() (15)
(15)
which is quadratic for any, provided, m
![]() (16)
(16)
The method of Equation (15) is also obtained by applying Newton’s method not to f, but rather to![]() . For
. For![]() , we obtain by the method of Equation (15) that requires not only
, we obtain by the method of Equation (15) that requires not only ![]() but also
but also![]() , starting with
, starting with![]() .
.
For ![]()
![]() (17a)
(17a)
For ![]()
![]() (17b)
(17b)
Equation (15) may be written as
![]() (18)
(18)
and it is of interest to know that
![]() (19)
(19)
For the price of a third derivative we may have the quadratic approximation
![]() (20)
(20)
6. An Erroneous m
The method
![]() (21)
(21)
produces the superlinear
![]() (22)
(22)
and if![]() , convergence is alternating.
, convergence is alternating.
7. Estimation of the Leading Term
We readily have that
![]() (23)
(23)
For example, for![]() , we compute using Equation (23) the
, we compute using Equation (23) the ![]() approximations as depending on the chosen x
approximations as depending on the chosen x
![]() (24)
(24)
8. An Elementary Discrete Two-Step Newton Method for Roots of Any Multiplicity
If
![]() (25)
(25)
are already close to root a of multiplicity![]() , then according to Equation (5)
, then according to Equation (5)
![]() (26)
(26)
nearly, from which we extract the approximation
![]() (27)
(27)
Setting a back into Equation (26) yields
![]() (28)
(28)
and the two-step method
![]() (29)
(29)
where ![]() in Equation (28) is seen to be but the finite-difference approximation of
in Equation (28) is seen to be but the finite-difference approximation of ![]() in Equation (14).
in Equation (14).
For example, for![]() , and starting with
, and starting with![]() , we compute by Equation (29), the successive approximations
, we compute by Equation (29), the successive approximations
![]() (30a)
(30a)
![]() (30b)
(30b)
![]() (30c)
(30c)
![]() (30d)
(30d)
Generally, starting with
![]() (31)
(31)
we have from the method of Equation (29) that
![]() (32)
(32)
The repeated classical Newton’s method, ![]() , we recall, is only linear if
, we recall, is only linear if ![]()
![]() (33)
(33)
See also [14] [15] .
9. Derivation of the Chord Method
It is a rational two step method of the form
![]() (34)
(34)
With
![]() (35)
(35)
the method is quadratic for ![]() and
and![]() . In fact;
. In fact;
For ![]()
![]() (36a)
(36a)
For ![]()
![]() (36b)
(36b)
For ![]()
![]() (36c)
(36c)
For ![]() the method produces
the method produces
![]() (37)
(37)
and for ![]() the method is quadratic for
the method is quadratic for ![]() as well.
as well.
According to Equation (36a), if![]() , then the method is higher than quadratic.
, then the method is higher than quadratic.
10. The Method is Further Superlinear
For ![]() we have:
we have:
For ![]()
![]() (38a)
(38a)
For ![]()
![]() (38b)
(38b)
For ![]()
![]() (38c)
(38c)
For ![]()
![]() (38d)
(38d)
For ![]()
![]() (38e)
(38e)
For ![]()
![]() (38f)
(38f)
For ![]()
![]() (38g)
(38g)
For ![]()
![]() (38h)
(38h)
For ![]()
![]() (38k)
(38k)
For ![]()
![]() (38l)
(38l)
11. Lowering the Value of k
We leave k in ![]() of Equation (34), free, and have by power series expansion, for multiplicity index
of Equation (34), free, and have by power series expansion, for multiplicity index![]() , for
, for ![]() in Equation (1), that
in Equation (1), that
![]() (39)
(39)
The linear term in the above expansion is annulled with
![]() (40)
(40)
We do this for higher values of m and find that
![]() (41)
(41)
We try![]() , and get
, and get
For ![]()
![]() (42a)
(42a)
For ![]()
![]() (42b)
(42b)
For ![]()
![]() (42c)
(42c)
For ![]()
![]() (42d)
(42d)
For ![]()
![]() (42e)
(42e)
For ![]()
![]() (42f)
(42f)
For ![]()
![]() (42g)
(42g)
For ![]()
![]() (42h)
(42h)
For ![]()
![]() (42k)
(42k)
For ![]()
![]() (42l)
(42l)
For ![]()
![]() (42m)
(42m)
The general form of the linear part of ![]() in Equations (42) is of the form
in Equations (42) is of the form ![]() with a constant
with a constant ![]() that is small if multiplicity index m is not much above 5. For instance,
that is small if multiplicity index m is not much above 5. For instance, ![]() , meaning that at each iteration the error
, meaning that at each iteration the error ![]() is reduced by this factor. Such convergence behavior we term superlinear. More concretely, for
is reduced by this factor. Such convergence behavior we term superlinear. More concretely, for![]() , we obtain by the above method, using
, we obtain by the above method, using![]() , starting with
, starting with![]() .
.
For ![]()
![]() (43a)
(43a)
For ![]()
![]() (43b)
(43b)
For ![]()
![]() (43c)
(43c)
12. Conclusions
The paper is predicated on the realistic assumption that the multiplicity index m of the iteratively targeted root is unknown. We conclude that if one prefers to shun second order derivatives, then the quadratic two-step method of Equation (29), that provides also ever better approximations for the multiplicity index m of the approached root, is a practically appealing alternative.
Otherwise, one may use the rational two-step method of Equation (34) with a constant k that is only slightly less than 2. Thus stating the method becomes superlinear, albeit, of a reduced speed of convergence for highly elevated root multiplicities. For the sake of brevity, the present paper does not explore the possibility of estimating the multiplicity index m of the sought root by the method of Equation (29), then applying this estimate to the choice of an optimal k in the method of Equations (34) and (35).