Received 25 April 2016; accepted 27 June 2016; published 30 June 2016

1. Introduction
Alumina (Al2O3) and Titania (TiO2) ceramics are popular materials used in plasma spray coating in manufacturing sector. The selection of coating material depends on the application of coating. Alumina is highly corrosion resistant and is used to resist abrasive wear. Al2O3-TiO2 coating is widely known as ceramic coating which shows strong addition to substrate, high dielectric strength, high wear strength and superior protection from corrosion. Ramachandran et al. [1] observe that TiO2 has a lower melting point and it actively combines with alumina grains, which results in to high density. So a coating of Al2O3-TiO2 composite supports the industry to get a hard, wear, oxidation and corrosion resistant coating on the surface of the subtract. EN24 is an alloy steel known as 34CrNiMo6 as per DIN and has Mn up to 0.7% in composition. EN24 is used in components such as gears, shafts, studs and bolts, and its hardness is in the range of 248 to 302 HB. EN24 can be further surface-hardened to create components with enhanced wear resistance by induction, coating or nitriding processing. EN24 possesses low corrosion resistance. An effective coating of Al2O3-TiO2 helps the EN24 steel surface to attain excellent corrosion resistance. A detailed survey of the research studies particularly in the field of Al2O3- TiO2 coatings and EN24 alloy steel applications is carried out in detail.
Yang et al. [2] presented the aspects of preparing of nanostructured Al2O3-TiO2-ZrO2 composite powders and plasma spraying nanostructured composite coating. Forghani et al. [3] utilized a design of experiment (DoE) method to identify the effect of air plasma spray (APS) parameters on several main properties of titanium dioxide (TiO2) coatings. Kang et al. [4] studied the influence of contact stress on rolling contact fatigue performance of plasma sprayed Al2O3-40% TiO2 composite ceramic coating using a double-roll test machine. Surface abrasion, spalling, and delamination were observed during this investigation. It was found that the initiation and propagation of fatigue cracks were mainly caused by the shear stress, which was highly influenced by the contact stress. Mishra et al. [5] deposited Al2O3-13TiO2 coating on nickel-based Superni 718 and AE 435 super alloys using a low-velocity oxy-fuel (LVOF) process. The coating was characterized for SEM, XRD and surface roughness. The LVOF sprayed Al2O3-13TiO2 coating had shown good oxidation resistance as well as adherence to the substrates under the tested environment.
Bolleddu et al. [6] deposited air plasma sprayed nanostructured Al2O3-13TiO2 coatings as a function of critical plasma spray parameter (CPSP), defined as the ratio of arc power to primary gas flow rate, using nitrogen and argon as the primary plasma gases. Effect of CPSP on microstructural and wear characteristics of coatings deposited with nitrogen was found to be relatively small. Morks et al. [7] carried out a detailed study of Al2O3-50% TiO2 composite coatings, which were sprayed on a mild steel substrate by using plasma spraying .Yugeswaran et al. [8] studied the Critical Plasma Spraying Parameter (CPSP) effect on plasma arc spraying to control the quality of coatings. Palacio et al. [9] coated AISI 1040 steel by atmospheric plasma spraying with 13% Al2O3 and 45% TiO2. Micro sized powders (6/22 and 13/41 μm) were used as raw materials for coating. Rico et al. [10] compared the mechanical and high temperature wear behavior of Al2O3-13% TiO2 nanostructured coatings to that of the conventional ones. Wang et al. [11] prepared Al2O3 coatings using supersonic plasma spraying on the porous Si3N4 substrate at the spraying power of 52, 54, 58 and 60 kW, respectively. The effect of spraying power on the microstructures and properties of Al2O3 coating was investigated. Vargas et al. [12] studied evolution of brine permeation in Al2O3-TiO2coatings elaborated by atmospheric plasma spray using Electrochemical Impedance Spectroscopy. Znamirowski et al. [13] investigated Titania composite layers made by atmospheric plasma spraying technique and laser engraving Emission characteristics of the emitters made of pure TiO2 and those made of Al2O3-13% TiO2.Vicent et al. [14] deposited Al2O3-13% TiO2 nanostructured and submicron-nanostructured powders using APS. Optimization of the deposition conditions enabled the reconstituted powders to be successfully deposited, yielding coatings that were well bonded to the substrate.
Murakami et al. [15] analysed the complicated fatigue data effects of non-metallic inclusion by adding spherical and angular alumina particles of various controlled sizes on Hard Chrome Coated EN24 Substrate. It was found that the geometrical parameter that controls the scatter of the fatigue strength is the square root of the projection area and not the shape of the inclusions. It is concluded that Fatigue strength of materials containing inclusions larger than a critical size can be predicted.
Ramesh et al. [16] studied Fretting wear behaviour of liquid nitrided structural steel, EN24. They had conducted tests at different normal loads on many bearing shaft assemblies and at constant slip amplitude under unlubricated conditions. Coefficient of friction under fretting conditions and wear resistance were measured. Surface chemistry influences the fretting wear behavior more than the hardness of the materials in the case of EN24. Sarmahet al. [17] investigated the wear mechanisms while machining EN24 steel having multiple coatings of TiC, Ti (C, N), TiN and AlON. It was concluded that the AlON coatings provide the best crater wear resistance under high speed cutting conditions for EN24. Tomlinson et al. [18] analysed running in wear of whiter layers formed on EN24 Steel by centerless grinding. The white layers increased the resistance of the steel to wear. The mechanism of wear was by abrasion and the results followed a simple truncation model.
Aparnadevi et al. [19] carried out a study which deals with an objective to implement different heat treatments such as annealing, normalizing and hardening with different quenchants (water and oil) to witness its effect on corrosion behaviour of selected EN8 and EN24 grades of steels. Normalizing, oil quenching and water quenching exhibit lesser degree of corrosion resistance compared to that of annealed specimen. EN24 grade of steel exhibited better corrosion resistance than EN8. Sabithaghosh et al. [20] studied the effect of various heat treatments on the mechanical properties of EN24 steel. Ball Indentation Technique has been used to evaluate the variation in mechanical properties due to heat treatment on EN24 steel. Increments in tempering temperature have softened the EN24 steel substrate and thus decreased the strength but increased strain hardening exponent. They reported some typical complicated aspects of the effects of non-metallic inclusions on the fatigue strength.
Mohandas et al. [21] Studied the Surface Integrity and Heat Measurement during Hard Turning of Hard Chrome Coated EN24 Substrate. The input parameters considered are spindle speed, feed, depth of cut, nose radius and cutting edge angle. EN24 substrate was coated with hexavalent chrome to a thickness of 170 μm. The surface hardness before and after hard turning of hard chrome plated surfaces were studied. The experimental results revealed that the maximum heat was observed at 2 mm from the cutting edge on the top diagonal.
A number of researchers had explored the effect of various parameters on the final response of atmospheric plasma spray in the last five years. Researchers have utilized DoE methods to different thermal spray processes and for different aspects of this field. Troczynski et al. [22] applied response surface methodology (RSM) on plasma spray of WC-12% Co powders to optimize their parameters. Steeper et al. [23] used a Taguchi method to study the effects of plasma processing conditions on properties of alumina-titania coatings. In another study, Pierlot et al. [24] had utilized full factorial designs for their thermal spray work and carried out a review on the design of experiment methodology for thermal spraying. The design of Hadmard matrix and RSM are discussed in detail. Li et al. [25] investigated the plasma spray process parameters with respect to deposition efficiency, porosity and micro hardness using a uniform design of experiment.
It is observed from the thorough literature review that work carried out on EN24 is very rare. The research was mostly related to heat treatment and case hardening. The method followed by many of the researchers globally to relate input parameters to output parameters is through different types of mathematical modeling. But very few attempts are made to create mathematical models to depict the relationships between the input and output parameters in the case of Al2O3-TiO2 coatings. The literature review clearly shows the need for a detailed study for the input parameter optimization of plasma spraying of Al2O3-TiO2 coatings with various weight% of TiO2 on different metal substrates. The modern optimization techniques applied in the current work are very effective to set appropriate process parameters on plasma spraying machines as it is a very critical step to ensure highest utilization of the resources with no compromise on quality as well as productivity.
2. Experimental Procedure, Preparation and Testing of Al2O3-40%TiO2 Coating
EN24 alloy steel is made with a dimension of 27 mm diameter and 3 mm thickness from a flat sheet using punching process to make test substrate sample pieces. Three samples are used to conduct each of the experiment, assembled in one cartridge. Al2O3-40%TiO2 in powder form supplied by H. C. Starck, USA is used for coating. Thorough sand blasting is carried out on all the samples to keep the sample surface active and clean for coating. Fused Alumina of grit size 60 µm is used as the sand blasting material. This is supplied by Carborundum Universal. Al2O3-40% TiO2 powder is deposited on the rotating substrates by using an SG 100 Plasma spray gun, supplied by Metco. The coating powder is preheated up to 110˚C to ensure the removal of moisture.
The experiments are conducted as per the design of experiments. The details of DoE are shown in Table 2. Some of the parameter values, which are kept constant during the entire experiment, are given below.
Once the coating process is over, the sample pieces are washed in ethanol and dried to avoid accumulation of moisture. Measurement of coating thickness is done with an ultrasonic thickness gauge. The surface roughness values are measured by surface roughness tester SV-C3100 by Mitutoyo Japan. The measurement is done on the coating surface for a length of 15 mm with a pitch of 0.001 mm and scanning speed was 2.0 mm/sec. Hardness tester make Equotip 3, with range of up to 1000 HV is used for hardness measurement
2.1. Experimental Design and Procedure
The experiment is carried out using L18 orthogonal array of Taguchi’s design of experiments (DoE). Selected responses in this study are surface roughness, coating thickness and hardness. The input parameters considered are distance of plasma spray gun, substrate rpm, arc current, coating power flow rate and carrier gas flow. The entire input parameters considered for the experiment along with levels decided are shown in Table 1.
The Design of Experiments is given in detail in Table 2.
2.2. Coating Output Parameter Details
The mean values of the measured coating thickness, roughness and hardness are given in Table 3.
3. Results and Discussion
Regression modelling is done using MS Excel’s data analysis capability for each of the output parameters. The derived mathematical models for output parameters are shown below as Equations (1)-(3).
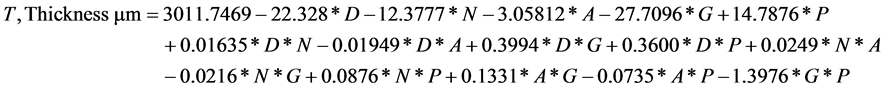 (1)
(1)
![]()
Table 2. DoE for conducting the experiments.
![]()
Table 3. The values of measured output parameters.
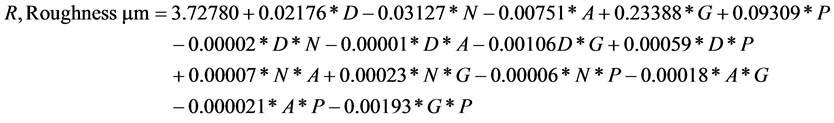 (2)
(2)
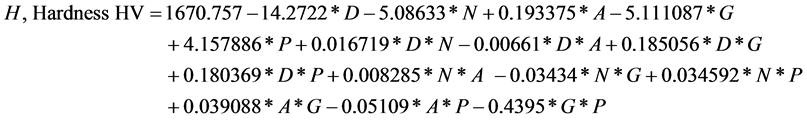 (3)
(3)
where
D = Spray distance,
N = Substrate RPM,
A = Arc Current,
G = Carrier gas flow, and
P = Powder flow rate.
The values of thickness and hardness are considered as beneficial (higher the better) and the values of thickness and hardness are considered as beneficial (lower the better). ANOVA is carried out on each of these models to check the adequacy as shown in Tables 4-6.
![]()
Table 4. Regression details and ANOVA of thickness model.
![]()
Table 5. Regression details and ANOVA of roughness model.
![]()
Table 6. Regression details and ANOVA of hardness model.
3.1. Confirmation Experiments
Confirmation tests are conducted with five samples .To conduct the test, random values are selected for all input parameters which lies between maximum and minimum levels. The final measurement of all output parameters are taken and shown in Tables 7-9 along with predicted values obtained using the proposed mathematical models. The % variation between actual and predicted values is also given in tables.
3.2. SN Analysis
Signal-to-noise ratio, or the SN ratio, is calculated for each set of experiments.SN ratio clearly indicates the effect of each input parameter on the desired output parameter. The values of SN ratios are tabulated as shown in Table 10 for each factor and level. The range ∆R (R = high SN-low SN) of the SN for each input parameter is found out. The larger the R value for an input parameter, the larger the effect that parameter has on the output parameter. That means, the same change in input parameter signal causes a larger effect on the output parameter is considered as most dominating.
SN ratio values for coating thickness are derived for each input parameters. The values are shown in Table 11.
Here, the R value clearly shows that spray gun distance has a dominating effect on the coating thickness. The next deciding parameter in the case of coating thickness is rpm of the EN24 substrate. The sequence of significance is shown as rank. Similarly, SN ratio values are calculated for surface roughness for each parameter and level for all the output parameters as shown in Table 12. It is found that arc current has a significant effect on the surface roughness. The next dominant parameter in the case of surface roughness is rpm of the substrate. In the case of surface hardness, the spray distance has a significant effect on the coating hardness as shown in Table 13. The next dominant parameter in the case of hardness is carrier gas flow. All the effects of input parameters vs SN Ratio means related to coating thickness, roughness and hardness are shown as graphs in Figures 1-3.
3.3. Application of Teaching Learning Based Optimization (TLBO)
Teaching-learning-based optimization (TLBO) is applied individually to each of the mathematical models of output parameters given by Equations (1) to (3) to derive the optimum values of output parameters. TLBO―an advanced optimization method―is a teaching-learning process inspired algorithm proposed by Rao et al. [26] , based on the effect of influence of a teacher on the output of learners in a class. Teacher and learners describes two basic modes of the learning, through teacher (known as teacher phase) and interacting with the other learners (known as learner phase). The algorithm mimics teaching-learning ability of teacher and learners in a class room. The algorithm-specific parameter-less concept of the algorithm is one of the attracting features of this procedure. The algorithm is very simple to use and it has an effective capability to provide the global or near
![]()
Figure 1. SN ratio vs input parameter in the case of coating thickness.
![]()
Figure 2. SN ratio vs input parameter in the case of coating roughness.
![]()
Figure 3. SN ratio vs input parameter in the case of coating hardness.
![]()
Table 7. Measured and predicted values―thickness.
![]()
Table 8. Measured and predicted values―hardness.
![]()
Table 9. Measured and predicted values―roughness.
![]()
Table 10. Levels and parameters SN ratio.
![]()
Table 11. SN ratio matrix and ∆R values of coating thickness.
![]()
Table 12. SN ratio matrix and ∆R values of coating roughness.
![]()
Table 13. SN ratio matrix and ∆R values of coating hardness.
global optimum solutions in comparatively less number of function evaluations. More details about the TLBO algorithm can be found in [27] and https://sites.google.com/site/tlborao. Another recently developed algorithm specific parameter-less algorithm known as Jaya [28] may also be attempted for optimization.
Pickard et al. [29] mentioned that the TLBO algorithm has origin bias affecting the population convergence and success rates of benchmark objective functions with origin solutions. But they had overlooked the fact that the TLBO algorithm provided better results even for the benchmark functions whose solutions were not located at the origin [27] [30] - [32] . Many researchers had obtained better results with TLBO algorithm for different objective functions with different characteristics. Moreover, the results shown by Pickard et al. [29] in Table 1 of their paper are checked by the first author of this paper under the same conditions and it is found that the results shown by Pickard et al. [29] for non-origin based objective functions were incorrectly reported. The TLBO algorithm has obtained the optimum results irrespective of whether the solution to the objective function is located at the origin or not. Comments were also made by Rao [32] on the unusual concept of function evaluations required for duplicate removal. Furthermore, Pickard et al. [29] mentioned that the bias is occurring when teaching factor takes the value of 2. But in the original TLBO algorithm, the value of teaching factor varies randomly during each iteration either as 1 or 2 and it will not remain as 2 during all the iterations and Pickard et al. [29] had not considered this fact. The TLBO algorithm has been applied by many researchers to many real life applications (whose solutions are not located at origin) in different engineering disciplines and obtained better results as compared to the other advanced optimization algorithms [32] .
In the present work, 30 independent runs with a population size of 10 and 100 number of iteration generations is considered for executing the TLBO algorithm for the optimisation of individual objective functions of output parameters. Optimized values obtained by applying TLBO algorithm for the individual objective functions of output parameters are: T (Thickness), R (Roughness) and H (Hardness) are 1476.0 µm, 4.1659 µm and 915.847 HV respectively. Convergence graphs of TLBO for each of the output parameters are displayed in Figures 4-6.
![]()
Figure 4. Convergence graph of TLBO for coating thickness.
![]()
Figure 5. Convergence graph of TLBO for coating roughness.
![]()
Figure 6. Convergence graph of TLBO for coating hardness.
3.4. Formation of Combined Objective Function
A combined objective function is formed by apirori approach, involving all the three objective functions. The Combined objective function is solved by applying TLBO algorithm for the given ranges of the input parameters. By considering only one objective at a time, the optimized values for individual output parameters T, R and H are already obtained by applying TLBO. However, practically, optimization of all these output parameters is required together simultaneously. That way, the problem becomes a multi-objective problem, as shown in Equation (4).
![]() . (4)
. (4)
In the above Equation (4) Tmax, Rmin and Hmax represents the optimum desired values T, R and H when solved individually for the given range of input parameters. These values are 1476.0 µm, 4.1659 µm and 915.847 HV respectively. W1, W2 and W3 show the weights assigned to the individual objective functions. The weights W1, W2 and W3 can be assigned by the researcher based on his experience, literature review and input from other experts. In this paper, a systematic approach of assigning the weights, known as Analytic Hierarchy Process (AHP) [33] is presented. This method lets the person to assign the weights by following the theory of relative importance. The numbers 3, 5, 7, and 9 correspond to the verbal judgments “moderate importance”, “strong importance”, “very strong importance”, and “absolute importance” is given. A parameter compared with itself is assigned the value 1 so, the main diagonal entries of the pair-wise comparison matrix are all 1. Decision making matrix is made as shown below comparing the output parameters, Coating thickness (T), Surface roughness (R) and Hardness (H).
![]()
The normalized weights of each output parameter is calculated following the procedure and these are WT = 0.1048, WR = 0.2583 and WH = 0.6370. The value of maximum Eigen value (lmax) is 3.0385 and consistency ratio (CR) = 0.036712, which is much less than the allowed CR value of 0.1. Thus, there is good consistency in the judgments made. The weights calculated following the AHP method are applied to the combined objective function as given below in Equation (5).
![]() (5)
(5)
Now, the TLBO algorithm is used to optimize the combined objective function and the optimum value of coefficient Zmax is achieved. Considering a population of 10 and after 30 independent runs and 100 iterations, The Zmax achieved is 0.2993and the corresponding values of the optimum input parameters are:
Spray distance: 75 mm,
Carrier Gas Flow: 40 Lit./min,
Powder flow rate: 25 Gms./min,
RPM of the substrate: 150 rpm,
Arc current: 500 A.
These input parameter values are simultaneously satisfying all the three objectives considered for Al2O3-40% TiO2 coating on EN24 substrate. The convergence graph of TLBO optimization process is shown as Figure 7.
The combined objective function is once again generated considering assumed weights, i.e., WT = 0.50, WR = 0.25 and WH = 0.25, and TLBO algorithm is applied on the combined objective function. The optimum value of coefficient Zmax is 0.0230and the corresponding values of optimum input parameters are:
Spray distance: 175 mm,
Carrier Gas Flow: 40 Lit./min,
Powder flow rate: 50 Gms./min,
RPM of the substrate: 350 rpm,
Arc current: 500 A.
From the convergence data of TLBO, it is concluded that there is a drastic change in the optimum input parameters derived, while changing the weights of individual objective function from AHP based one to equal weights. Two parameters, “Spray distance”, “substrate rpm” and “powder flow rate” are shifting from minimum to maximum in the case of equal weights. The convergence graph of TLBO is shown as Figure 8.
4. Conclusion
Research work in field of ceramic coating on EN4 alloy steel is rarely seen. In the field of surface coating with Al2O3-40% TiO2, mathematical modeling and optimization are also very rare. In the present work, regression analysis is used to generate mathematical models for all the output parameters. The confirmation tests are carried out
![]()
Figure 7. Convergence graph of TLBO for the combined objective function.
![]()
Figure 8. Convergence graph of TLBO for combined objective function with equal weights of objectives.
NOTES
![]()
*Corresponding author.