A Multivariate Student’s t-Distribution

Daniel T. Cassidy

Department of Engineering Physics, McMaster University, Hamilton, ON, Canada.

DOI: 10.4236/ojs.2016.63040                

Abstract

A multivariate Student’s t-distribution is derived by analogy to the derivation of a multivariate normal (Gaussian) probability density function. This multivariate Student’s t-distribution can have different shape parameters for the marginal probability density functions of the multivariate distribution. Expressions for the probability density function, for the variances, and for the covariances of the multivariate t-distribution with arbitrary shape parameters for the marginals are given.

Keywords

Multivariate Student’s t, Variance, Covariance, Arbitrary Shape Parameters

Received 29 March 2016; accepted 14 June 2016; published 17 June 2016

1. Introduction

An expression for a multivariate Student’s t-distribution is presented. This expression, which is different in form than the form that is commonly used, allows the shape parameter 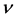for each marginal probability density function (pdf) of the multivariate pdf to be different.

The form that is typically used is 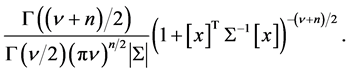[1]

(1)

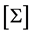This “typical” form attempts to generalize the univariate Student’s t-distribution and is valid when the n marginal distributions have the same shape parameter. The shape of this multivariate t-distribution arises from the observation that the pdf for is given by Equation (1) when is distributed as a multivariate normal distribution with covariance matrix and 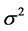is distributed as chi-squared.

The multivariate Student’s t-distribution put forth here is derived from a Cholesky decomposition of the scale matrix by analogy to the multivariate normal (Gaussian) pdf. The derivation of the multivariate normal pdf is given in Section 2 to provide background. The multivariate Student’s t-distribution and the variances and covariances for the multivariate t-distribution are given in Section 3. Section 4 is a conclusion.

2. Background Information

2.1. Cholesky Decomposition

A method to produce a multivariate pdf with known scale matrix 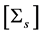is presented in this section. For nor- mally distributed variables, the covariance matrix 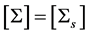since the scale factor for a normal distribution is the standard deviation of the distribution. An example with is used to provide concrete examples.

Consider the transformation where 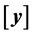and are column matrices, is square matrix, and the elements of are independent random variables. The off-diagonal elements of introduce correlations between the elements of.

(2)

The scale matrix. The covariance matrix has elements where is the expectation of and. If the are normally distributed, then , where the superscript T indicates a transpose of the matrix. If is known, then is the Cholesky decomposition of the matrix [2] .

For the example of Equation (2),

(3)

From linear algebra,. For as defined in Equation (2),

and whereas is the va- riance of the zero-mean random variable and is the covariance of the zero-mean

random variables and.

2.2. Multivariate Normal Probability Density Function

To create a multivariate normal pdf, start with the joint pdf for n unit normal, zero mean, independent random variables:

(4)

where is an n-row column matrix:. gives the probability that the random variables lie in the interval.

The requirement for zero mean random variables is not a restriction. If, then is a zero mean random variable with the same shape and scale parameters as.

Use Equation (2) to transform the variables. The Jacobian determinant of the transformation relates the products of the infinitesimals of integration such that

(5)

The magnitude of the Jacobian determinant of the transformation is (Appendix)

(6)

where the equality has been used.

Since, , and since, the multivariate “z-score”

becomes, which equals since for

normally distributed variables.

The result is that the unit normal, independent, multivariate pdf, Equation (4), becomes under the trans- formation Equation (2)

(7)

where is a n-row column matrix: and.

For the example,

(8)

from which can be calculated. In Equation (8),

(9)

The denominator in the expression for is.

3. Multivariate Student’s t Probability Density Function

A similar approach can be used to create a multivariate Student’s t pdf. Assume truncated or effectively truncated t-distributions, so that moments exist [3] [4] . For simplicity, assume that support is where b is a positive, large number, is the scale factor for the distribution, and is the location parameter for the distribution. If b is a large number, then a significant portion of the tails of the distribution are included. If then all of the tails are included.

Start with the joint pdf for n independent, zero-mean (location parameters) Student’s t pdfs with shape parameters, and scale parameters:

(10)

with. gives the probability that a random draw of the column matrix from the joint Student’s t-distribution lies in the interval. The pdf is a function of only and the shape parameter, and thus is independent of any other,.

Use the transformation of Equation (2) to create a multivariate pdf

(11)

The solution of the transformation Equation (2) was used. The elements of the inverse

matrix, , are given in terms of the by Equation (8) for the example. Note that the shape parameters of the constituent distributions need not be the same in the multivariate t-distribution given by.

gives the probability that a random draw of the column matrix from the multivariate Student’s t-distribution with shape parameters lies in the interval.

From the definition of the exponential function where is Euler’s number, then

(12)

and

(13)

In the limit as, the multivariate Student’s t-distribution, Equation (11), becomes a multivariate normal distribution.

3.1. Some for the Example

In this subsection some examples for the variances and covariances of a multivariate Student’s t-distribution using the example of Equation (2) are given.

The variance of the random variable is

(14)

with the limits of the integrations equal to and,.

Perform the integrations as listed. The integral over is unity since only depends on (c.f. Equation (2)) and factors into a product―see Equation (10). Write

(15)

(16)

where the are the elements of the inverse of matrix and are as given by, Equation (8), and is a constant as far as the integral over is concerned.

Repeat the procedure for the integrals for, , and. These integrals are not equal to unity owing to the presence of the term.

The variance of the random variable for the multivariate Student's t-distribution with support and with for all i is given by

(17)

The expression for is valid only for. The expression would be valid for if the region of support was rather than where is a scale factor and [3] - [5] . Note that the scale factors for the multivariate t-distribution are.

Truncation or effective truncation of the pdf keeps the moments finite [3] - [5] . For example, the second central moment for a Student’s t-distribution with scale factor and support is

(18)

which is finite provided that.

In the interest of brevity, only variances and covariances that were calculated for support of will be discussed. The requirement that will be understood to be waived if the pdf is truncated or effectively truncated. It is also to be understood that the variances and covariances as calculated for support of provide upper limits for variances and covariances calculated for truncation or effective truncation of the pdf.

If the are not equal, then for the example of Equation (2)

(19)

The covariance for the for all i is given by

(20)

If the are not equal, then the covariance

(21)

The expression for, which is valid for the not equal, is

(22)

The expressions for, , and show a simple pattern for the relationship between the covariance matrix, the scale matrix Equation (3), and the matrix Equation (2).

3.2. General Expressions for

Given a matrix that is an square matrix with elements, an expression for the variance (assuming support, for all i, and) for the multivariate Student’s t-distribution is

(23)

A general expression for the covariance (assuming support, for all i, and) for the multivariate Student’s t-distribution is

(24)

If support is, then the general expressions need to be multiplied by functions that depend on b and. Truncation or effective truncation keeps the moments finite and defined for all [3] - [5] . The general expressions for the covariance, Equation (24), yields, when, the general expression for the variance, Equation (23). The general expression for the variance, Equation (23), is given to emphasize the nature of the variance.

Unlike normally distributed random variables, the correlation matrix for random variables that are distributed as Student’s t is not equal to. For normally distributed variables, the scale parameter equals the standard deviation. For Student’s t distributed variables, the standard deviation does not equal the scale parameter. For a Student’s t distribution with shape parameter, scale parameter, and support,. If the region of support for the Student’s t distribution is truncated to then the variance for all and is finite for all [3] - [5] .

Given a matrix of the variances and the covariances, , and a column matrix of the shape parameters associated with each variable, the scale matrix would in principle be determined sequentially, starting with and. The shape parameters would be obtained from the marginal distributions or from other knowledge.

4. Conclusion

A multivariate Student’s t-distribution is derived by analogy to the derivation for a multivariate normal (or Gaussian) pdf. The variances and covariances for the multivariate t-distribution are given. It is noteworthy that the shape parameters of the constituent Student’s t-distributions of the multivariate t-distribution, Equation (11), need not be the same.

Acknowledgements

This work was funded by the Natural Science and Engineering Research Council (NSERC) Canada.

Appendix: The Jacobian

The Jacobian determinant is used in physics, mathematics, and statistics. Many of these uses can be traced to the Jacobian determinate as a measure of the volume of an infinitesimially small, n-dimensional parallelepiped.

1. Volume of a Parallelepiped

The volume of an n-dimensional parallelepiped is given by the absolute value of the determinant of the com- ponents of the edge vectors that form the parallelepiped.

The area of a parallelogram with edge vectors and is.

The volume of a parallelepiped with edge vectors, , and is given by the determinant

(25)

2. Inversion Exists

Assume that there are n functions. The necessary and sufficient condition that the func- tions can be inverted to find is that the Jacobian determinant is nonzero, i.e.,

(26)

where

(27)

To simplify the notation, assume that so that,. The total differential is

(28)

These equations can be put in matrix form

(29)

These three equations can be solved for the if the determinant of the matrix is non-zero. This is a standard result from linear algebra. The determinant of the matrix is called the Jacobian determinant of the transformation.

3. Change of Variables

The Jacobian determinant of the transformation is used in change of variables in integration:

(30)

The absolute value sign is required since the determinant could be negative (i.e., the volume could decrease).

The Jacobian determinant for the inverse transformation (to obtain as functions of) given by Eq- uation (8) is

(31)

which equals

(32)

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kotz, S. and Nadarajah, S. (2004) Multivariate t-Distributions and Their Applications. Cambridge University Press, Cambridge.
[2]	Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. (1992) Numerical Recipes in FORTRAN: The Art of Scientific Computing. 2nd Edition, Cambridge University Press, Cambridge, 89.
[3]	Cassidy, D.T. (2011) Describing n-Day Returns with Student’s t-Distributions. Physica A, 390, 2794-2802. http://dx.doi.org/10.1016/j.physa.2011.03.019
[4]	Cassidy, D.T. (2012) Effective Truncation of a Student’s t-Distribution by Truncation of the Chi Distribution in a Mixing Integral. Open Journal of Statistics, 2, 519-525. http://dx.doi.org/10.4236/ojs.2012.25067
[5]	Cassidy, D.T. (2016) Student’s t Increments. Open Journal of Statistics, 6, 156-171. http://dx.doi.org/10.4236/ojs.2016.61014