New Asymptotical Stability and Uniformly Asymptotical Stability Theorems for Nonautonomous Difference Equations

Abstract

New theorems of asymptotical stability and uniformly asymptotical stability for nonautonomous difference equations are given in this paper. The classical Liapunov asymptotical stability theorem of nonautonomous difference equations relies on the existence of a positive definite Liapunov function that has an indefinitely small upper bound and whose variation along a given nonautonomous difference equations is negative definite. In this paper, we consider the case that the Liapunov function is only positive definite and its variation is semi-negative definite. At these weaker conditions, we put forward a new asymptotical stability theorem of nonautonomous difference equations by adding to extra conditions on the variation. After that, in addition to the hypotheses of our new asymptotical stability theorem, we obtain a new uniformly asymptotical stability theorem of nonautonomous difference equations provided that the Liapunov function has an indefinitely small upper bound. Example is given to verify our results in the last.

Share and Cite:

Zhang, L. and Zhang, C. (2016) New Asymptotical Stability and Uniformly Asymptotical Stability Theorems for Nonautonomous Difference Equations. Applied Mathematics, 7, 1023-1031. doi: 10.4236/am.2016.710089.

Received 15 April 2016; accepted 4 June 2016; published 7 June 2016

1. Introduction

Difference equations usually describe the evolution of certain phenomena over the course of time. These equations occur in biology, economics, psychology, sociology, and other fields. In addition, difference equations also appear in the study of discretization methods for differential equations. Realizing that most of the problems that arise in practice are nonlinear and mostly unsolvable, the qualitative behaviors of solutions without actually computing them are of vital importance in application process. The stability property of an equilibrium is the very important qualitative behavior for difference equations. The most powerful method for studying the stability property is Liapunov’s second method or Liapunov’s direct method. The main advantage of this method is that the stability can be obtained without any prior knowledge of the solutions. In 1892, the Russian mathematician A.M. Liapunov introduced the method for investigating the stability of nonlinear differential equations. According to the method, he put forward Liapunov stability theorem, Liapunov asymptotical stability theorem and Liapunov unstable theorem, which have been known as the fundamental theorems of stability. Utilizing these fundamental theorems of stability, many authors have investigated the stability of some specific differential systems [1] - [9] .

We know that several results in the theory of difference equations have been obtained as more or less natural discrete analogues of corresponding results of differential equations, so Liapunov’s direct method is much more useful for difference equations. Actually, some authors have utilized the methods for difference equations successfully [10] - [20] . Using the method, S. Elaydi [10] and J.P. Lasalle [11] gave the classical Liapunov stability theorem for autonomous difference equations. In [12] [13] , the authors extended the technique to generalized nonautonomous difference equations and put forward the classical Liapunov stability theorem for nonautonomous difference equations. In [14] - [17] , the direct approach was extended to some special delay difference systems to investigate the stability properties. In [18] - [20] , how to construct Liapunov function for difference system or hybrid time-varying system was exploited.

Consider the following nonautonomous difference system

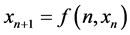(1.1)

where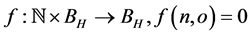, 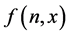is continuous in x and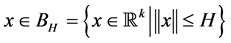. As shown in [12] [13] , using Liapunov’s direct method to study the asymptotical stability of the zero solution of system (1.1) relies on the existence of a positive definite Liapunov function 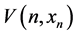which has indefinitely small upper bound and whose variation 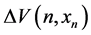along the solution of system (1.1) is negative definite.

Sometimes it is not easy to determine the positive definite Liapunov function for a given equations in applications. If we further require that the function has indefinitely small upper bound besides its negative definite variation, the work would become more difficult to do. In this paper, we weaken the Liapunov function to positive definite and also weaken the negative definite variation to semi-negative definite on orbits of Equations (1.1), then we put forward a new Liapunov asymptotical stability theorem for difference Equations (1.1) by adding to extra conditions on the variation. Subsequently, provided that all the conditions of our new asymptotical stability theorem are satisfied, we obtain a new uniformly asymptotical stability theorem of nonautonomous difference equations if the Liapunov function has an indefinitely small upper bound.

2. Some Lemmas

In this section, we introduce the following lemmas, which play a key role in obtaining our results.

Lemma 1 Suppose that there exists a function 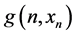satisfying the following conditions:

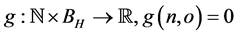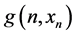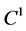(i), is with respect to the second argument x,

(ii) the sequence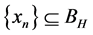, and

(iii) 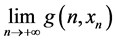exists.

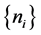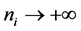Then, there exists a positive integer sequence with as 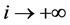such that

.

Proof. We first prove that for arbitrary constant there exists a sufficient large integer for every positive integer such that

(2.1)

Suppose that this conclusion of inequality (2.1) does not hold, then there exist such that for arbitrary there exists a positive integer such that

(2.2)

By the continuity of, we obtain that either or. Without loss of generality, we only consider the first case. For the above, there exists a positive integer increasing sequence such that for arbitrary. Let denote a constant. By the discrete analogue fundamental theorem of calculus [10] , we get

Note that is a positive integer increasing sequence and, then the above inequality contradicts

to the exists of Therefore, the conclusion of (2.1) is proved.

Denote with By the conclusion of (2.1), for each i, there exists a sufficiently large

such that

(2.3)

for each positive integer. Then we can select special and construct an increase sequence

. This implies as and

Lemma 2 Assume that there exists a function satisfying the following conditions:

(i), is with respect to the second argument,

(ii) the sequence, and

(iii) exists.

Then, for each fixed r, there exists a positive integer sequence with as such that

Proof. We first prove that for arbitrary constants there exists a sufficient large integer such that for every there exists

(2.4)

The case of is proved by (2.1) in the proof of Lemma 2.1. Suppose that inequality (2.4) holds in the case of but is not true in the case of r. Then there exist constants such that for arbi-

trary there exists a positive integer such that. Similarly to the state-

ment below inequality (2.2), there exists a positive integer sequence such that.

Let denote the maximum integer not exceeding x and denote a constant. Same as above, without loss of generality, we only consider the case. By the discrete analogue fundamental theorem of calculus [10] , we get

(2.5)

where.

(2.6)

where.

If and, from inequality (2.5), we obtain

(2.7)

If and, from inequality (2.6), we obtain

(2.8)

Inequalities (2.7) and (2.8) imply that

(2.9)

Since as, we select. This leads to a contradiction because of the inductive assumption for (2.4) in the case of. Therefore, the conclusion of (2.4) is proved.

Similarly to the second part of the proof of Lemma 2.1, for each r, we can construct a sequence

with as such that This completes the proof of Lemma 2.2.

According to Lemma 2.2 we prove the following result.

Lemma 3 Assume that there exists a function satisfying the following conditions:

(i), is and is uniformly continuous with respect to the second argument x,

(ii) the sequence, and

(iii) exists.

Then, there exists a positive integer sequence with as such that

(2.10)

Proof. Let us first prove

(2.11)

Suppose that this is not true. Then there exist a constant c > 0 and a strictly increasing integer sequence

such that as and,. By the uniform continuity of, there exists a constant, when for any, then. From the above inequalities, we get. This is a contradiction to (2.4). Then equation (2.11) is proved.

The result of (2.11) implies the boundedness of on. It follows that is

uniformly continuous on the same domain. And as shown above, we obtain Then we see recursively that

(2.12)

On the other hand, by Lemma 2.2, there exists a sequence with as such that

(2.13)

From (2.12) and (2.13) we easily get (2.10). The proof of Lemma 2.3 is complete .

3. New Asymptotical Stability and Uniformly Asymptotical Stability Theorems

In this section, we propose and prove the new asymptotical stability and uniformly asymptotical stability theorems of system (1.1). First of all, we introduce a special class of function and then give the definition of positive definite function. Subsequently, we introduce the various stability notions of the equilibrium point of system (1.1). These definitions are very useful for obtaining our results besides the above Lemmas.

Definition 1 A function is said to be class of K if it is continuous in, strictly increasing, and.

Definition 2 The function is positive definite if there exists a function such that

for all.

Definition 3 Let be an initial condition of system (1.1) and be a solution such that. The equilibrium point of system (1.1) is said to be:

(i) Stable if given and there exists such that implies

for all, uniformly stable if may be chosen in dependent of.

(ii) Attracting if there exists such that implies, uni-

formly attracting if the choice of is independent of.

(iii) Asymptotically stable if it is stable and attracting, and uniformly asymptotically stable if it is uniformly stable and uniformly attracting.

Theorem 1 Consider nonautonomous difference Equations (1.1), where is with respect to the second argument x and satisfies. Suppose that there exists a positive definite function such that

(i),

(ii), where,

(iii) is bounded on the set,

(iv), where the func- tion defined by Definition 1.

Then the zero solution of system (1.1) is asymptotically stable.

tion with satisfies

By condition (ii) we know that is monotonically nonincreasing. Hence the exists.

From condition (iii) we know that is bounded, which implies that is uniformly con- tinuous. According to Lemma 3, there exists a integer sequence with as such that

(3.1)

According to the definition of function and Equation (3.1), we get, which implies

(3.2)

Now we prove

(3.3)

Suppose that (3.3) is not true. Then there exist a constant and an integer sequence with as such that . Then, by the definition of positive definite

(3.4)

On the other hand, by (3.2) there is an integer j such that. This is because V is continuous with respect to the second argument and Thus, by condition (ii), for all. Clear, for sufficiently large l such that, which contradicts to the definition of v given

by (3.4). Therefore, (3.3) is proved. According to Definition 3, we obtain that the zero solution of system (1.1) is asymptotically stable.

In addition to the hypotheses of Theorem 1, we can obtain that the zero solution of system (1.1) is uniformly asymptotically stable if has an indefinitely small upper bound as in the classical Liapunov asymptotical stability theorem of nonautonomous difference equations.

Theorem 2 Provided that the hypotheses of Theorem 1 are satisfied, the zero solution of system (1.1) is uniformly asymptotically stable if positive definite function has an indefinitely small upper bound.

Proof. Since is positive definite and has an indefinitely small upper bound, there exist functions

such that for all. For each, there exists a

such that. Denote and, then we have for all. If

this is not true, then there exists a such that and imply. However,

implies that for. Then we obtain that

This is a contradiction. Since all the conditions of Theorem 1 are satisfied, the zero solution of system (1.1) is

asymptotically stable. Therefore, for the above, , there exists when.

4. Example

In this section, we provide an example to illustrate the feasibility of our results.

Example 4.1. Consider the following difference equations

(4.1)

where and. Obviously,

f is C1 with respect to on and satisfies Denote and. This function which satisfies is clearly positive definite on and is along the solutions of system (4.1), and

(4.2)

Moreover,

For and, we obtain, then the zero solution of system (1.1) is stable. At the same condition, we also get

Now, we calculate. For, we have

Then we get, which means that is bounded on the set. Now, we only need to verify the example whether satisfies condition (iv) of

Theorem (3.1). Denote,. Then is a class of K function. From the above analysis, we obtain

Then,

Thus condition (iv) of Theorem (3.1) is fulfilled. The zero solution of Example 4.1 is asymptotical stable. Inequation (4.2) implies that has an indefinitely small upper bound. Then the zero solution of Example 4.1 is also uniformly asymptotically stable.

We also can utilize Polar coordinate transformation to prove the above conclusion. Let and, then system (4.1) transforms the following form:

(4.3)

The square of the first equation adding the square of the second equation in system (4.3) yields

Denote and we get Under the conditions of and, we obtain and. By Definition 3, we obtain the zero solution of the

original system (4.1) is asymptotical stable and uniformly asymptotically stable. This confirm the correctness of utilizing Theorem 3.1 and Theorem 3.2 to judge Example 4.1.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No.31170338), the General Project of Educational Commission in Sichuan Province (Grant No.16ZB0357) and the Major Project of Sichuan University of Arts and Science (Grant No.2014Z005Z).

NOTES

*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1] Melvin, W. (1975) Liapunov’s Direct Method Applied to Neutral Functional Differential Equations. Journal of Mathematical Analysis and Applications, 49, 47-58.
http://dx.doi.org/10.1016/0022-247X(75)90161-4
[2] Leipholz, H. (1984) An Alternative to Liapunov’s Stability Method and Its Application to Higher-Order Systems. Computer Methods in Applied Mechanics and Engineering, 47, 299-314.
http://dx.doi.org/10.1016/0045-7825(84)90081-1
[3] Noldus, E. and Loccufier, M. (1994) An Application of Liapunovs Method for the Analysis of Neural Networks. Journal of Computational and Applied Mathematics, 50, 425-432.
http://dx.doi.org/10.1016/0377-0427(94)90318-2
[4] Xu, R., Chaplain, M. and Davidson, F. (2004) Persistence and Global Stability of a Ratio-Dependent Predator-Prey Model with Stage Structure. Applied Mathematics and Computation, 158, 729-744.
http://dx.doi.org/10.1016/j.amc.2003.10.012
[5] Ionescu-Kruse, D. (2007) Liapunov’s Direct Method for Birkhoffian Systems: Applications to Electrical Networks. Journal of Geometry and Physics, 57, 2213-2228.
http://dx.doi.org/10.1016/j.geomphys.2007.06.005
[6] Shi, R. and Chen, L. (2008) Staged Structured Lotka-Volterra Predator-Prey Models for Pest Management. Applied Mathematics and Computation, 203, 258-265.
http://dx.doi.org/10.1016/j.amc.2008.04.032
[7] Zhang, L. and Zhang, C. (2010) Rich Dynamic of a Stage-Structured Prey-Predator Model with Cannibalism and Periodic Attacking Rate. Communications in Nonlinear Science and Numerical Simulations, 15, 4029-4040.
http://dx.doi.org/10.1016/j.cnsns.2010.02.009
[8] Fu, S., Zhang L. and Hu, P. (2013) Global Behavior of Solutions in a Lotka-Volterra Predator-Prey Model with Preystage Structure. Nonlinear Analysis: Real World Applications, 14, 2027-2045.
http://dx.doi.org/10.1016/j.nonrwa.2013.02.007
[9] Hamada, Y. (2014) Liapunov’s Stability on Autonomous Nuclear Reactor Dynamical Systems. Progress in Nuclear Energy, 73, 11-20.
http://dx.doi.org/10.1016/j.pnucene.2013.12.012
[10] Elaydi, S. (2005) An Introduction to Difference Equations. 3rd Edition, Springer, New York.
[11] Lasalle, J. (1976) The Stability of Dynamical Systems. Siam, Philadelphia.
http://dx.doi.org/10.1137/1.9781611970432
[12] Agarwal, R. (2000) Difference Equations and Inequations. 2nd Edition, Marcel Dekker, Inc., New York.
[13] Lakshmikantham, V. and Trigiante, D. (2002) Theory of Difference Equations Numerical Methods and Application. 2nd Edition, Marcel Dekker, Inc., New York.
http://dx.doi.org/10.1201/9780203910290
[14] Zhang, S.N. (2001) Stability of Neutral Delay Difference Systems. Computers and Mathematics with Applications, 42, 291-299.
http://dx.doi.org/10.1016/S0898-1221(01)00154-7
[15] Zhang, S. and Zheng, G. (2002) Almost Periodic Solutions of Delay Difference Systems. Applied Mathematics and Computation, 131, 497516.
http://dx.doi.org/10.1016/S0096-3003(01)00165-5
[16] Wei, G. and Shen, J. (2010) Boundedness and Asymptotic Behavior Results for Nonlinear Difference Equations with Positive and Negative Coefficients. Computers and Mathematics with Applications, 60, 2469-2475.
http://dx.doi.org/10.1016/j.camwa.2010.08.046
[17] Wei, G. (2011) Asymptotic Behavior Results for Nonlinear Neutral Delay Difference Equations. Applied Mathematics and Computation, 217, 7184-7190.
http://dx.doi.org/10.1016/j.amc.2011.02.004
[18] Giesl, P. (2007) On the Determination of the Basin of Attraction of Discrete Dynamical Systems. Journal of Difference Equations and Applications, 13, 523-546.
http://dx.doi.org/10.1080/10236190601135209
[19] Giesl, P. (2008) Construction of a Local and Global Lyapunov Function for Discrete Dynamical Systems Using Radial Basis Functions. Journal of Approximation Theory, 153, 184-211.
http://dx.doi.org/10.1016/j.jat.2008.01.007
[20] Malisoff, M. and Mazenc, F. (2008) Constructions of Strict Lyapunov Functions for Discrete Time and Hybrid Timevarying Systems. Nonlinear Analysis: Hybrid Systems, 2, 394-409.
http://dx.doi.org/10.1016/j.nahs.2006.12.005

Journals Menu
Follow SCIRP
Contact us
customer@scirp.org
WhatsApp +86 18163351462(WhatsApp)
Click here to send a message to me 1655362766
Paper Publishing WeChat

Copyright © 2025 by authors and Scientific Research Publishing Inc.

Creative Commons License

This work and the related PDF file are licensed under a Creative Commons Attribution 4.0 International License.