Strategic Economic Partnerships, Exchange Rate Policy and Agricultural Trade: A Gravity Model Analysis of China’s Agricultural Trade Flows ()


1. Introduction
Since its accession into the World Trade Organization (WTO) in 2001, China’s influence on global agricultural trade has significantly increased. China is a leading global producer of agricultural products namely pork, rice, vegetables, fruits and cotton, it is largely self-sufficient with the exception of a few commodities it imports [1]. In the period under review China has greatly opened up its Agricultural trade sector through proactive involvement in a number of regional and international trade agreements. This coupled with a shift in government agricultural policy has led to consistent agricultural trade growth. The main question this study seeks to explore is which factors influence China’s agricultural trade flows and what affects its choice of agricultural trading partner to ensure the full exploitation of comparative advantage for selected commodities. In recent years Gravity model application on China’s Agricultural trade sector has focused more on estimating the potential gains of Regional integration particularly in relation to the China-Association of Southeast Asian Nations Free Trade Area (CAFTA). Concluding that China’s agricultural trade sector will benefit significantly from such agreements particularly in agricultural commodities in which it has a comparative advantage such as vegetables, wheat and horticultural products [2]. There has however been limited research work to confirm such forecasts and predictions.
Our estimation results are consistent with expectations in relation to economic size, market size, distance, exchange rate and strategic economic partnership status of China and its trading partners. Results also show that China’s domestic agricultural policy framework is enabling enhanced agricultural trade through the stimulation of domestic demand. However, China’s maintained strong import momentum in agriculture is a phenomenon that has been received with mixed reactions by policy makers. Our study is split into 6 main sections including the introductory part. The second section gives a detailed outline of our research hypotheses including a thorough review of literature on gravity model applications in bilateral trade analysis. The third section gives the reader more information regarding the nature of our data and data sources. Our model specification and detailed methodology are given in the fourth section. The firth section contains estimation results and discussions. The last section offers a brief summary and conclusion of the main thrust of our study.
2. Research Hypotheses
2.1. Development of Gravity Model Analysis in Trade Analysis
The Gravity model was initially regarded as a mere empirical stable relationship between economic size, distance and the volume of trade between nations. With the more prominent models in trade analysis being the Heckscher-Ohlin (HO) model and the Ricardian Model. The later attributed differences in trade activities across nations to differences in technology while the HO model was based on the varying factor endowments that exist between nations. Whilst the HO model appeared to be more superior to the earlier Ricardian model it was not without its limitations, with the greatest critic to this model being the work of [3] whose empirical results totally contradicted the HO model giving rise to what was later to be coined the Leontief Paradox. Though Gravity Model empirical work predated theory, many researchers have been able to prove that the models fundamental assumptions can be derived from a range of trade theories [4]. According to [5] the theoretical basis for Gravity Model application in international trade analysis can be derived from earlier trade models like the Ricardian and the factor proportions theory or HO model. Other empirical studies including [6] and [7] have also shown that the Gravity Model can be derived from both the Ricardian and HO models. Research on the theoretical base of the Gravity Model is still undergoing however its explanatory power in trade analysis has proved invaluable.
2.2. Gravity Model Specification in Sectoral Analysis
Well estimated Gravity models control for relative trade costs between nations [8]. The rationale behind most Regional and International trade agreements is to promote trade by lowering trade costs that exist between nations. Agricultural trade is unique in that every nation has its own domestic agricultural policy even if there are involved in the same regional or international trade agreement. Agriculture is a sensitive sector where the tradeoffs between self-reliance and self-sufficiency goals are often felt the most. China’s agricultural trade report for 2012 indicates that China’s agricultural trade sector has experienced significant growth in the past 2 decades. However, factors that have attributed to this growth are still subject to research. Gravity Model specifications utilized in international trade analysis are based on a multiplicative equation as derived from Newtonian physics. When natural logarithms of this equation are taken it yields the following basic form of the Gravity Model equation:
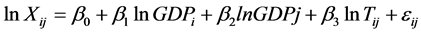 (1)
(1)
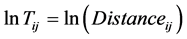 (1a)
(1a)
where:
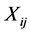 denotes the monetary value of trade between nation i and nation j.
denotes the monetary value of trade between nation i and nation j.
β0 Is a regression constant.
β1-3 are regression coefficients.
GDPi denotes the Gross Domestic Product of country i.
GDPj denotes the Gross Domestic Product of country j.
Tij is the distance in between country i and country j.
From the above basic form of the Gravity Model equation it can be concluded that countries with larger economic sizes in terms of GDP are expected to trade more but countries that are further apart in terms of distance are expected to trade less due to inferred higher trade costs. Recent studies have adopted a number of variables to capture trade costs between nations. Tariff barriers and other associated trade costs are often captured in the Gravity model through dummy variables for regional and international trade agreements Gravity Model application in analyzing sectoral trade flow data is not entirely straightforward, [9] suggest that as economies grow in size trade expands both at the extensive margin and intensive one. This means as that countries do not only trade more products but also a greater volume of each product. It is this realization that makes Gravity model applications in disaggregated data problematic because economic size (GDP) and market size (population) are not always good estimates of demand. China started to shift from an export oriented economy to a more domestic demand driven one since its entry into the WTO. It began to open up its huge domestic market for imports thus providing great opportunities for its regional and international trading partners [10]. How this has affected agricultural trade is still not fully understood. With the expectation being that agricultural trade will increase particularly for labor intensive agricultural commodities were China has a comparative advantage due to relatively lower labor costs.
2.3. China’s Agricultural Trade Sector
Since 2004 government support in China’s agricultural sector has grown significantly, in line with its shift in agricultural policy the government of China began to support agriculture instead of taxing the sector to promote industrial development [1]. This coupled with low labor costs is expected to enhance the competitiveness of Chinese agricultural products. However, according to [1] there are also a number of factors that weaken the competitiveness of China’s agricultural products namely its land tenure system, its fragmented transportation and cold storage infrastructure. There have been a number of trade studies that have utilized the Gravity model to explain bilateral trade flows between countries. In a recent study to analyze Vietnam’s trade activities utilizing the Gravity model [11] found that the economic size of Vietnam, economic size and market size of foreign partners, distance and culture have huge effects on bilateral trade flows between Vietnam and its trading partners.
Most Gravity model studies in recent years have focused on the impact of regional and international trade agreements on aggregate bilateral trade. In a study to estimate the potential benefits of CAFTA to China’s agricultural sector [2] concludes that CAFTA will improve resource allocation between countries involved and boost agricultural trade. Our study focus is to ascertain the Gravity model factors that influence China’s agricultural trade sector and ascertain the extent to which its strategic economic partnership and exchange rate policy have influenced agricultural trade flows with its major trading partners for selected agricultural commodities. Our research Hypotheses based on the above review of literature are as follows:
1. Economic size and market size have a positive influence on agricultural trade.
2. The devaluation of China’s currency will positively influence agricultural trade flows.
3. Regional Integration Agreements (CAFTA) and Strategic economic partnership agreements (BRICS) have a positive influence on China’s agricultural trade flows.
3. Data
This study utilizes secondary data collected from three major sources. Panel data on agricultural trade between China and 10 of its top agricultural trading partners was obtained from the UN Comtrade database. The agricultural trade values are an aggregation of the following commodities: bovine meat, pork or swine meat, poultry meat, fish, potatoes, wheat, maize/corn, rice and tobacco. The data is collected for the 15 years spanning from year 2000 to year 2014. GDP and population statistics were obtained from the World Bank Development Indicators database. The GDP is used to represent the economic size of nation. Population is defined as the total number of people living in a particular nation or geographical area, and in Gravity model specification it re- presents the market size of a nation. Exchange rate data was obtained from the IMF International Financial Statistics database. The exchange rate value represents the annual average market exchange rate value in relation to the US dollar. Distance between capitals was obtained from the website www.chemical-ecology.com. The distance variable is reported in kilometers. It is used to capture trade costs or barriers to trade in Gravity model specifications.
Regional integration agreement status or strategic economic partnership status of trading partners with China was obtained from a number of online sources. The 2 main regional integration agreement or strategic economic partnerships that are considered in this study are CAFTA and BRICS. With the later being an economic partnership between the top 5 developing nations. The acronym BRICS stands for Brazil Russia India China and South Africa. This economic partnership has made great progress since its inceptions both in terms of fostering better economic and diplomatic ties. It has also advocated for increased trade between the nations involved.
4. Methodology
To analyze the factors that influence China’s agricultural trade flows the study utilizes a variation of the Gravity model similar to the work of [12]. Our model will control for multilateral terms of resistance or country effects by including dummy variables to capture the impact of regional integration agreements, strategic partnership agreements, cultural beliefs and language. Agricultural production is subject to a number of local factors or sectoral idiosyncrasies hence sectoral trade flows are more heterogeneous than aggregate ones. This paper utilizes the following specification of the Gravity model expressed in natural logarithmic form:
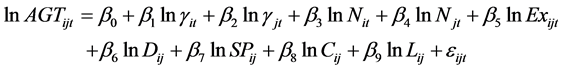 (2)
(2)
The variables in the above stated model denote the following:
i: Country 1 (China)
j: 2, 3, 4, 5, 6, (Partner Countries)
t: 2000, 2006, 2007….2014.
AGTijt: China’s Agricultural Trade with country j in year t
Yit: China’s GDP in year t
Yjt: GDP of partner j in year t
Nit: Population of country i (China) in year t
Njt: Population of partner j in year t
Dij: Distance between Capitals of China and country j
Exijt: Exchange rate between China and country j in year t
SPij: Dummy variable showing whether partner country is part of a strategic economic partnership agreement with China. (1 = both in a strategic economic partnership, CAFTA/BRICS 0 = Not in any strategic economic partnership)
Cij: Dummy variable for common cultural beliefs (1 = trading partner has common or similar cultural beliefs with China, 0 = different cultural beliefs)
Lij: Dummy variable for language (1 = trading partner shares a common language with China, 0 = no common language)
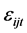 : Error term
: Error term
The criterion variable is agricultural trade flow values for the following commodities as aforementioned in Section 3, bovine meat, pork, poultry, fish, potatoes, wheat, maize, rice and tobacco. The value is the sum of both exports and imports between China and its trading partners in the period under review. The independent variables for economic size are GDP values, as reported by the World Bank Development Indicators database. The population variable is also obtained from the World Bank Development Indicators database. It is a good approximate of the market size of China’s agricultural trading partners. Market size is a variable that captures the demand side of the Gravity model just like GDP of the partner country. The distance between capitals, namely the distance between Beijing and the capital cities of its major agricultural trading partners is used as a proxy to measure trade costs or barriers.
The Annual average market exchange rate data obtained from the IMF International Financial Statistics website represents the average value of a currency in relation to the US dollar. To make these values relevant to our model a simple transformation is made. Which involves dividing China’s annual average exchange rate in relation to the US dollar with its trading partners’ annual average exchange rate in relation to the US dollar to obtain an estimate of the annual average exchange rate between China and its trading partners. The exchange rate variable is expected to give an inference on what would happen to agricultural trade flows between China and its trading partner if China decided to devalue its currency. The Regional Integration Agreement status or strategic economic partnership variable is a control variable aimed at measuring the impact of China’s strategic economic partnerships on bilateral agricultural trade. This study only focuses on two main strategic partnership agreements BRICS and CAFTA. Our model also controls for language and cultural beliefs. The function represents the trade cost element of our Gravity model specification.
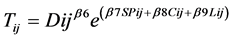 (3)
(3)
Estimation Approach
The use of panel data in econometric analysis has a number of advantages like the ability to analyze variables at many levels referred to as multilevel or hierarchical modeling. However, the main advantage relevant to this study is the fact that panel data allows researchers to control for variables that cannot be easily observed or measured [13]. The main approaches used in panel data econometric analysis are the random effects model (REM) and the fixed effects model (FEM). FEM controls for time invariant differences between individual entities, it is mainly used when the main research interest is to analyze the impact of predictor variables that vary over time. This exclusion of time invariant factors introduces bias to the fixed effects model particularly in the analysis of slow changing variables. FEM assumes that a particular factor within an entity may impact or bias the predictor outcome [14]. FEM also excludes the effects of time invariant characteristics as aforementioned, this is mainly to more effectively assess the net effect of predictor variables on the criterion variable. The key insight in the fixed effect model is that if the unobserved variable does not change over time, then any changes in the dependent variable must be due to influences other than these fixed characteristics [15].
The crucial distinction between fixed and random effects is whether the unobserved individual effect embodies elements that are correlated with the regressors in the model, not whether these effects are stochastic or not [16]. The random effects model assumes that the variation across entities is random and uncorrelated with the predictor or independent variables within the model. This allows for the inclusion of time invariant variables, which are absorbed in the intercept when applying the fixed effects model. Based on the above discussion our study utilized a random effects FGLS regression approach corrected for cross sectional correlation and heteroscedasticity across panels. To test the presence of random effects in our model we conducted a Breusch and Pagan Lagrangian multiplier test for random effects. To test for cross sectional correlation, we conducted a Breusch-Pagan LM test and utilized an LR test for heteroscedasticity across panels.
5. Estimation Results
We conducted a Breusch and Pagan Lagrangian multiplier test for random effects (LM test) to ascertain the best approach to estimate our Gravity Model equation. The null hypothesis in the LM test is that the variances across entities is zero. This means that there is no significant difference across units hence no panel effect. The results of this test are presented in Table 1.
Based on the above results, the null hypothesis is rejected. Hence our estimation results are based on the random effects model. To test for the presence of heteroskedasticity and contemporaneous correlation we conducted the LR test and Breusch-Pagan LM test of independence respectively (see Appendix). Both tests confirmed the presence of cross sectional dependence and heteroscedasticity across panels. To correct for these, we used the FGLS estimator with contemporaneous correlation and heteroskedasticity across panels (Table A2).
The estimation results presented in Table 2 show that the predictor variables which influence China’s bilateral agricultural trade flows with major trading partners are China’s GDP (Yit), GDP of partner country (Yjt), market size measured as population (Nit, Njt), the distance between capitals of China and partner countries (Dij), annual average exchange rate between China and partner countries (Exijt), regional integration or strategic partnership status between China and trading partner (SPijt), cultural beliefs (Cij) and language (Lij).
![]()
Table 1. Breusch and Pagan Lagrangian multiplier test for random effects.
Note: ***Statistically significant at 1%; H0: There is no significant difference across units/no panel effect.
Note: *** Significant at 1%; Criterion variable: AGTijt China’s Agricultural Trade with Partner j in year t.
5.1. Impact of Economic Size on China Agricultural Trade Flows
The impact of economic size on China’s agricultural trade flows is consistent with Gravity Model expectations. Which is economic size having a positive significant effect on bilateral trade flows between countries. China’s GDP coefficient is 0.2353528 significant at 1%. This value is interpreted as elasticity; a 1 percent increase in China’s GDP will lead to a 0.24% increase in agricultural trade flows with its major trading partners. Likewise, the economic size of China’s trading partners has a positive impact on agricultural trade flows for selected commodities in the period under review. The coefficient for GDP of partner country variable is 0.3201635 significant at 1%. This means that a 1 % increase in China’s trading partner GDP will enhance agricultural trade by 0.32%. China’s largest agricultural trading partner is the USA both these countries have large economic sizes in terms of GDP. This confirms our initial hypothesis on the influence of economic size on agricultural trade flows.
5.2. The Impact of Market Size on Agricultural Trade
The market size variables (population of China and the population of its trading partners) have a positive influence on agricultural trade flows which is in tandem with gravity model expectations. The coefficient for China’s population variable is 6.989024 which are significant at 1%, indicating that a 1% increase in China’s population will enhance agricultural trade flows by 6.9%. The population variable for China’s trading partners is 0.5467775 significant at 1%. This shows that a 1% increase in the populations of China’s major agricultural trading partners will enhance agricultural trade flows by 0.54%. China has become a net importer of agricultural commodities with its major trading partner being the USA, whose population is about a one third of China’s population.
5.3. Impact of Devaluation of China’s Currency
The devaluation of a currency is expected to make a country’s exports more competitive to its trading partners ceteris paribus. In this study the coefficient for the exchange rate variable is 0.136038, which is significant at 1%. It indicates that if China devalues its currency by one percent this will have a positive influence on agricultural trade flows with its major trading partners. Enhancing agricultural trade in selected commodities by 0.13%. This is in tandem with our second hypothesis. The distance variable in Gravity Model estimation captures the barriers or cost of trade between nations. The expectation as mentioned in Section 4 is that the greater the geographical distance between nations is the less they are expected to trade. This is because distance enhances the cost of trade between nations. In our estimation the coefficient for distance is −1.133529 significant at 1%. This is consistent with gravity model expectations that distance negatively influences trade. A 1% increase in geographical distance between China and its trading partners will reduce agricultural trade flows by 1.13%. Therefore, China is expected to trade more with countries in the same region.
5.4. The Impact of CAFTA and BRICS Membership Status
In our study we focused mainly on two strategic partnership agreements, namely CAFTA and BRICS. The regional integration status variable in our Gravity Model specification was introduced as a control variable. The coefficient for the control variable is 0.9825723 significant at the 1%. However, it is not interpreted directly as an elasticity. To be interpreted as an elasticity it must first undergo the following mathematical transformation:
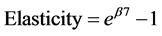 (4)
(4)
Transforming the coefficient of the regional integration status control variable results in the following elasticity value 1.6713. Therefore, in the period under review CAFTA and BRICS membership status had a positive influence on agricultural trade flows between China and its major trading partners. Enhancing trade value by up to 1.67% in the period under review. This result validates our final hypothesis. Therefore, it can also be concluded that China has been very efficient in the implementation of its Regional Integration Agreements particularly CAFTA or strategic partnerships (BRICS), with regards to fostering greater agricultural trade both regionally and internationally. Cultural beliefs and language proved to be significant variables in explaining agricultural bilateral trade flows between China and its major trading partners. Both control variables were significant at the 99% level of significance. Cultural beliefs had a negative influence on agricultural trade with a transformed coefficient of −0.6188. The language variable positively influenced trade with a transformed coefficient of 1.35.
6. Conclusion
The main purpose of the study was to ascertain the factors that influence China’s agricultural trade flows. A number of studies have been conducted utilizing the Gravity Model in bilateral trade analysis however a limited number of studies have focused on China’s agricultural trade sector. In this study we were able to ascertain that economic size, market size, regional integration or economic partnership status, language integration and devaluation of China’s currency all have a positive influence on its agricultural trade flows with major trading partners in the study period. Geographical distance and cultural beliefs proved to have a negative influence on agricultural trade for selected commodities. The estimates above are not entirely conclusive due to a number of econometric problems associated with panel data econometric manipulation as well as inherent limitations of Gravity Model application in trade analysis [17]. One limitation of the FGLS estimator as employed in this study is that it often leads to optimistic standard error estimates [18]. However, despite these limitations we believe this paper provides great insight on the role of exchange rate policy, regional integration or strategic economic partnerships, cultural beliefs and language integration on China’s bilateral agricultural trade flows. Which will prove valuable for policy makers and future researchers on China’s agricultural trade sector.
Appendix
![]()
Table A1. Breusch-Pagan LM test of independence (cross sectional dependence).
***Significant at 1% strongly reject H0; H0: There is no cross sectional correlation across panels.
![]()
Table A2. Likelihood-ratio test for heteroskedasticity
***Significant at 1% strongly reject H0; H0: Homoskedastic.