Growth of Graphene Nanocoil in a SiC Container: A Molecular Dynamics Study

Swastibrata Bhattacharyya¹, Shotaro Otake¹, Shota Ono¹, Riichi Kuwahara², Kaoru Ohno¹

¹Department of Physics, Yokohama National University, Tokiwadai, Japan.
²Dassault Systèmes BIOVIA K.K., ThinkPark Tower, Osaki, Japan.

DOI: 10.4236/ampc.2016.65012                

Abstract

Graphene nano structures find their application in modern nano electronics because of their excellent mechanical, unique electronics and electrical properties owing to the ballistic transport, where the charge carriers can move freely without getting scattered. In this work, we show a possibility to grow a miniaturised coil from a pre-existing graphene coil layer using molecular dynamics simulation. From our calculations it was observed that isolated carbon atoms get attached to the edge of the initial graphene coil and form an extension of the coil structure. The growth process depends strongly on the chirality of the growth front as well as the growth temperature. An optimal temperature between 2000 - 2300 K was proposed for all the edge structures except armchair (2500 K) type for the maximum number of the new hexagonal rings. Our results predict a technique that can be adopted experimentally to grow graphene nanocoil.

Keywords

Graphene Coil, Molecular Dynamics, Growth, SiC

Received 25 March 2016; accepted 9 May 2016; published 12 May 2016

1. Introduction

Graphene, a planar and atomically thin two dimensional material, experimentally discovered [1] just over a decade ago, posses many remarkable electronic properties along with interesting optical, mechanical and thermal properties. This results in an extensive research field of this wonder material from the fundamental world in physics and chemistry to the applications’ world in modern technology. The ability to pattern graphene [2] - [4] into various nano structures such as nanoflakes and nanoribbons in a controlled way makes this material a promising candidate for nano electronic devices. Graphene has better electrical properties such as high electron mobility (~2 × 10⁵ cm²∙V⁻¹∙s⁻¹ [5] ) and high current carrying capacity [6] compared with the conventional conducting material like copper. The high electric conductivity and strong mechanical properties of graphene, verified experimentally [1] [7] [8] indicate a possibility to replace copper as interconnects and induction coils in integrated circuits and other nano devices. Miniaturised coils can not only be used in radio frequency com- munication circuits as high-performance electromagnetic wave absorbers but also in sensors and magnetic beam generators too [9] - [11] . Carbon micro/nanocoils have been experimentally synthesised and show magnetic sensing ability [12] . However, a graphene nanocoil would have a different coil structure made of a spiral graphene plane and can be a low dimensional and effective alternative to the usual planar coiled inductors. If it can be really made experimentally, the excellent electrical properties is predicted to produce a very large mag- netic field (~1 T) and show superior inductance compared to present microelectronics devices [13] . In addition, these kinds of planar spiral structures are interesting in mathematics as well as in natural science such as topological insulators. It has been reported theoretically that the graphene spirals show Rashba splitting, a distinct topological signature in its electronic structure [14] .

One still not has succeeded in producing such a structure artificially, but there has been an experimental evidence in the presence of the screw dislocations in natural graphite showing a spiral growth pattern [15] . An abundant screw dislocation has been reported in pyrolytic graphites annealed at high temperature [16] . This indicates the stability of such spiral structure and the possibility to synthesise experimentally. The purpose of this paper is to theoretically explore a possibility of creating such a graphene nanocoil artificially by carrying out a molecular dynamics simulation. We opted to use SiC as the container since it has advantage over other sub- strates for its use in high temperature and high frequency electronics applications. Chemical vapour deposition (CVD) is one of the methods of depositing high quality graphene on various metal substrates [17] [18] and has been used to grow epitaxial graphene on SiC [19] [20] . In CVD, the substrate is exposed to the precursor in a gas state from where the C atoms gets attached to the substrate and the growth of graphene takes place. We would like to explore the growth of a spiral graphene nanocoil from a starting graphene spiral layer inside a hollow container made of SiC, where the coil is exposed to isolated C atoms falling from outside.

2. Computation Method

2.1. The Model System

For this purpose, we assume that graphene nanocoil is growing inside an insulating or semiconducting cylindrical container that has a pillar at the center and a flat bottom. The coil will be formed around the pillar as shown in Figures 1(a)-(c). Here brown indicates insulating/semiconducting pillar and cylinder; and sky blue and dark blue indicate monolayer and double layer graphene parts, respectively. The red square indicates the growth front, where carbon atoms are selectively absorbed. If this growth front is grown step-by-step by the increment of one column made of a single chain of hexagonal rings, we can expect that the growth front keeps having the same structure as the time increases, although the angle and the position change time to time as shown in Figure 1(b). This is similar to a “mathematical induction”-like growth mechanism. This means, if the growth front is grown by one column at the initial time t₀ to form the “one-column grown” growth front at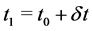, then the growth front at any later time t is grown by an increment of a single column to form the new growth front at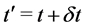. This assumption is based on the fact that the radius of the coil is large enough and a small portion near the growth front can be viewed similar to a graphene nano ribbon. Thus, by exposing the growth front to the isolated C atoms we can expect to have a continuously growing uniform spiral structure of graphene till the required length of the coil is obtained. We want to verify theoretically whether this assumption is a realistic one by using computer simulation as described in the next section.

2.2. Molecular Dynamics Simulation

For the simulation we have constructed a SiC cylindrical container of inner (outer) radius of 22.14 (26.5) Å and a pillar of radius 5.3 Å at the centre. The base plane inside the SiC cylinder is a (0001) plane over which we place a starting layer of the graphene coil around the pillar which mimics the pre-existing screw dislocation in graphite. The corresponding atomic structure is shown in Figure 1(d). The isolated C atoms are placed randomly near the growth front of the coil. Since the system has a large number of atoms, we have used classical

Figure 1. Top view of the graphene coil growth model (a) at an initial time and (b) at a later time. (c) Side view of the model structure. (d) Side view of the actual structure having a graphene coil inside a SiC container with a pillar at the centre. The C (of SiC) and Si atoms are shown in grey and purple colours while the C atoms of the graphene coil are shown in blue.

molecular dynamics simulation for all the calculations using the GULP code [21] in Materials Studio software package [22] . We adopted Tersoff potential [22] for silicon and carbon to describe the atomic interactions. Canonical (NVT) ensemble, where substance (N), volume (V) and themperature (T) are conserved was con- sidered for the system and the simulation was done at a constant temperature using Nose-Hoover thermostat. All the atoms in the SiC substrate and the starting graphene coil were constrained to be fixed throughout the simulation unless mentioned otherwise. No such constraint was applied to the additional C atoms, letting them relax and get attached to (or move away from) the growth front for each temperature. Each structure was simulated for 20 ps, with a time step of 1 fs. Using such a molecular dynamics simulation, we study the growth of the graphene nanocoil at various temperatures and predict a suitable temperature for any future application.

We assume classical harmonic oscillator to estimate atomic vibration at a given temperature T and found that the amplitude of the thermal vibration is 0.16 - 0.22 Å around the experimental condition from 1300 K to 2500 K. The present study assumes such high temperatures, so that correlation between neighboring atoms can be ignored. This selected range of temperature is justified as there is experimental report for growth of graphene sheet on SiC substrate using CVD at ~1900 K [19] .

3. Results and Discussion

We have considered an armchair line along the radius of the coil as the reference direction shown in Figure 2(a). With respect to this line we cut the coil at various angles to construct the starting graphene structure resulting in growth fronts having different chiralities. We name these growth fronts (GF) by the angle θ. The top view of the starting graphene coil for 30˚ edge is shown in Figure 2(a). We have considered a total of six such growth fronts: GF-10, GF-20, GF-40 and GF-50 along with a zig zag (θ = 30˚) (GF-zz) and an armchair (θ = 60˚) (GF-ac) ones. Isolated C atoms are placed near these edges along the same plane as the graphene coil near the growth fronts. The edge structures for all the growth fronts together with the starting random configuration of the isolated C add-atoms are shown in Figure 2(b). We have adopted different colour convention for the C atoms to

Figure 2. (a) Top view of the starting graphene coil for with θ = 30˚. C atoms of the bottom layer in the overlapping region is represented by grey balls. The reference (armchair) direction is shown by the black horizontal arrow. θ denotes the angle at which the coil has been cut to form the growth front. (b) Growth fronts constructed for θ = 10˚ (GF-10), 20˚ (GF-20), 30˚ (GF-zz), 40˚ (GF-40), 50˚ (GF-50) and 60˚ (GF-ac) are shown along with the isolated add atoms for the starting configuration in each case. Different colours represent the growth front (green), the bulk portion (blue) and the isolated add atoms (in orange), respectively.

distinguish bulk graphene, growth front and the add-atoms.

Inserting these starting structures in the SiC cylinder with an inner pillar as explained in Figure 1, we perform molecular dynamics simulation at temperatures of 1000 K, 1300 K, 1500 K, 1800 K, 2000 K, 2300 K and 2500 K for each structure. We analyse the final structures after completion of time of 20 ps for all the growth temperature conditions. Some of the isolated C atoms get attached to the growth front while others move away from the SiC cylinder. The attached C atoms form hexagonal, heptagonal and pentagonal rings or broken rings near the edge. We observe a strong dependence of the number and type of C rings on temperature as well as the structure of the starting growth front. Formation of hexagonal carbon rings is an indication of possibility to grow a defect free graphene coil farther. The presence of rings other than hexagonal one also shows a possibility of growing graphene coils with defect. With the increase in temperature, the number of C atoms getting attached at the growth front increases till an optimal temperature is reached after which either this number decreases or the resulting structure deforms. The growth front GF-40 has a comparatively poor attachment of the isolated C atoms throughout the temperature range considered in this work. Considering the number of hexagonal rings formed at the growth front as the parameter to predict the possibility of growing a good quality graphene nanocoil, we count the number of rings of all the final structures and plot it with respect to the corresponding growth temperature. These plots are shown in Figures 3(a)-(f). All these plots indicate that the number of newly formed hexagonal ring peaks at a particular (or a range of) temperature that varies with the growth front type. Among all the structures GF-zz and GF-50 have the maximum number of hexagonal rings at the optimal temperature, while GF-40 shows poor attachment of C atoms at all temperatures. The optimal temperature lies within the range of 2000 K - 2300 K for all the growth fronts except GF-ac, where the optimal temperature is achieved at 2500 K. The best final structures after the simulation is shown in the inset of each graphs in Figure 3 at the corresponding optimal temperature. In GF-zz, GF-ac and GF-20 we see a uniform growth of one column of hexagonal ring. This verifies our initial assumption of growing the coil in an increment of hexagonal chain, preserving the initial structure of the growth front. Similar growth is observed in other growth fronts too.

We repeated the calculation for few of these structures at selected temperatures by removing the constraints on all the C atoms in the graphene coil. This represents a more realistic structure where all the C atoms vibrate near their equilibrium position. We observe formation of hexagonal rings at the growth front and the graphene coil retains its structure. However, the final structure is not exactly same as the one obtained by fixing all the C atoms of the starting graphene coil. For comparison, we plot the number of newly formed hexagonal rings when the graphene coil is not fixed with respect to the growth temperature for GF-zz in Figure 4(a) along with the final structure at temperature 2300 K in the inset. Both the Figure 3(c) and Figure 4(a) show that the number of

Figure 3. Plots of the number of newly formed hexagonal carbon rings at different growth temperature have been shown for (a) GF-10, (b) GF-20, (c) GF-zz, (d) GF-40, (e) GF-50 and (f) GF-ac. The final structure at the simulation time of 20 ps has been shown for the maximum number of newly formed hexagonal ring in the inset of the corresponding plots. Similar convention as that of Figure 2 has been followed for C atoms.

Figure 4. (a) Plot of the number of newly formed hexagonal carbon rings at different growth temperature for GF-zz when no constraint of motion was applied to the atoms of the starting graphene coil. The final structure at the simulation time of 20 ps has been shown for 2300 K in the inset. (b) The structure of the graphene coil inside the SiC cylinder at 40 fs for isolated C atoms placed over the graphene coil sheet away from the growth front at growth temperature of 2000 K. Similar convention as that of Figure 1 and Figure 2 has been followed for all the atoms.

hexagonal ring has two peaks: one at around 1000 K (1300 K) and another at around 2000 K (2300 K) for constrained (non constrained) graphene coil. This indicates a slight shift in the two maxima towards higher growth temperature when the constraint is removed. The final structure at 2300 K in Figure 4(a) contains one hexagonal ring less than that of Figure 3(c). The structure shows a tendency to form hexagonal rings if more C atoms are added towards the right end of the growth front, where two incomplete rings exist. Thus, our simulation predicts that graphene nanocoil can be produced in experiments from a starting layer of graphene coil inside a SiC substrate if the optimal growth condition is met corresponding to the initial structure.

Next, we perform simulation by putting carbon atoms on top of the graphene coil sheet away from the growth front to rule out the possibility of forming graphene nano flake over the graphene coil, which will eventually hamper further growth of the coil. We have to explore this possibility, as whole graphene surface except the overlapping bottom layer is exposed to isolated C atoms inside the SiC cylinder. We observe that for the temperature range used in this work, carbon atoms placed on a terrace of graphene nanocoil evaporate and fly out of the SiC cylinder (Figure 4(b)). Thus, at such high temperatures, carbon atoms placed on a terrace far from the growth front are detached and attached repeatedly, and after some time, if they come close to the growth front, they will be absorbed to form new hexagonal rings.

4. Conclusion

We have proposed a way to create a graphene nanocoil from a pre-existing layer. Our prediction is motivated from the growth of coils from a pre-existing screw dislocations in bulk graphite. Using classical molecular dynamics simulations, we have shown that when isolated carbon atoms are placed near the growth front of the coil they get attached to form extension of the graphene coil by forming mostly hexagonal rings along with a few number of hepta and/or pentagonal rings in some conditions. The newly formed structure near the growth front is very sensitive to the chirality of the pre-existing edge as well as the growth temperature. All the growth fronts, studied in this work, show an optimal temperature at which the number of newly formed hexagonal ring is the maximum. This optimal temperature varies with the starting structure and lies between 2000 - 2500 K. The number of hexagonal rings at the optimal temperature is maximum for the growth fronts having angles of 30˚ (zig-zag) and 50˚ as measured from the armchair direction, thus making them ideal growth fronts. At every temperature, isolated carbon atoms placed away from the growth front will be detached. Thus by choosing the right temperature one can successfully synthesise a graphene nanocoil inside a SiC cylinder with a central pillar from a pre-existing coil layer using experiments such as CVD. With the advancement of growing and patterning graphene on substrates in the modern technology one can surely construct the first graphene layer inside the insulating or semiconducting cylinder.

Acknowledgements

This work has been supported by the HPCI promoted by MEXT (Project ID: hp150231).

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Novoselov, K. S., Geim, A.K., Morozov, S.V., Jiang, D., Zhang, Y., Dubonos, S.V., Grigorieva, I.V. and Firsov, A.A. (2004) Electric Field Effect in Atomically Thin Carbon Films. Science, 306, 666-669. http://dx.doi.org/10.1126/science.1102896
[2]	Sahin, R., Simsek, E. and Akturk, S. (2014) Nanoscale Patterning of Graphene through Femtosecond Laser Ablation. Applied Physics Letters, 104, 053118. http://dx.doi.org/10.1063/1.4864616
[3]	Ye, Y., Gan, L., Dai, L., Dai, Y., Guo, X.F., Meng, H., Yu, B., Shi, Z.J., Shang, K.P. and Qin, G.G. (2011) A Simple and Scalable Graphene Patterning Method and Its Application in CdSe Nanobelt/Graphene Schottky Junction Solar Cells. Nanoscale, 3, 1477-1481. http://dx.doi.org/10.1039/c0nr00999g
[4]	Kotakoski, J., Brand, C., Lilach, Y., Cheshnovsky, O., Mangler, C., Arndt, M. and Meyer, J.C. (2015) Toward Two-Dimensional All-Carbon Heterostructures via Ion Beam Patterning of Single-Layer Graphene. Nano Letters, 15, 5944- 5949. http://dx.doi.org/10.1021/acs.nanolett.5b02063
[5]	Bolotin, K.I., Sikes, K.J., Jiang, Z., Klima, M., Fudenberg, G., Hone, J., Kim, P. and Stormer, H.L. (2008) Ultrahigh Electron Mobility in Suspended Graphene. Solid State Communications, 146, 351-355.
[6]	Moser, J., Barreiro, A. and Bachtold, A. (2007) Current-Induced Cleaning of Graphene. Applied Physics Letters, 91, 163513. http://dx.doi.org/10.1063/1.2789673
[7]	Yan, Z., Lin, J., Peng, Z.W., Sun, Z.Z., Zhu, Y., Li, L., Xiang, C.S., Samuel, E.L., Kittrell, C. and Tour, J.M. (2012) Toward the Synthesis of Wafer-Scale Single-Crystal Graphene on Copper Foils. ACS Nano, 6, 9110-9117. http://dx.doi.org/10.1021/nn303352k
[8]	Lee, C.G., Wei, X.D., Kysar, J.W. and Hone, J. (2008) Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science, 321, 385-388. http://dx.doi.org/10.1126/science.1157996
[9]	Wang, G.Z., Gao, Z., Tang, S.W., Chen, C.Q., Duan, F.F., Zhao, S.C., Lin, S.W., Feng, Y.H., Zhou, L. and Qin, Y. (2012) Microwave Absorption Properties of Carbon Nanocoils Coated with Highly Controlled Magnetic Materials by Atomic Layer Deposition. ACS Nano, 6, 11009-11017. http://dx.doi.org/10.1021/nn304630h
[10]	Bell, D.J., Sun, Y., Zhang, L., Dong, L.X., Nelson, B.J. and Grützmacher, D. (2006) Three-Dimensional Nanosprings for Electromechanical Sensors. Sensors and Actuators A: Physical, 130-131, 54-61.
[11]	Pan, L.J., Zhang, M. and Nakayama, Y. (2002) Growth Mechanism of Carbon Nanocoils. Journal of Applied Physics, 91, 10058-10061. http://dx.doi.org/10.1063/1.1471575
[12]	Kato, Y., Adachi, N., Okuda, T., Yoshida, T., Motojima, S. and Tsuda, T. (2003) Evaluation of Induced Electromotive Force of a Carbon Micro Coil. Japanese Journal of Applied Physics, 42, 5035. http://dx.doi.org/10.1143/JJAP.42.5035
[13]	Xu, F.B., Yu, H., Sadrzadeh, A. and Yakobson, B.I. (2016) Riemann Surfaces of Carbon as Graphene Nanosolenoids. Nano Letters, 16, 34-39. http://dx.doi.org/10.1021/acs.nanolett.5b02430
[14]	Avdoshenko, S.M., Koskinen, P., Sevincli, H., Popov, A.A. and Rocha, C.G. (2013) Topological Signatures in the Electronic Structure of Graphene Spirals. Scientific Reports, 3, 1632.
[15]	Horn, F.H. (1952) Spiral Growth on Graphite. Nature, 170, 581. http://dx.doi.org/10.1038/170581a0
[16]	Hennig, G.R. (1965) Screw Dislocations in Graphite. Science, 147, 733-734. http://dx.doi.org/10.1126/science.147.3659.733
[17]	Li, X.S., Cai, W.W., An, J., Kim, S., Nah, J., Yang, D.X., Piner, R., Velamakanni, A., Jung, I., Tutuc, E., Banerjee, S.K., Colombo, L. and Ruoff, R.S. (2009) Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils. Science, 324, 1312-1314. http://dx.doi.org/10.1126/science.1171245
[18]	Kim, K.S., Zhao, Y., Jang, H., Lee, S.Y., Kim, J.M., Kim, K.S., Ahn, J.-H., Kim, P., Choi, J.-Y. and Hong, B.H. (2009) Large-Scale Pattern Growth of Graphene Films for Stretchable Transparent Electrodes. Nature, 457, 706-710. http://dx.doi.org/10.1038/nature07719
[19]	Strupinski, W., Grodecki, K., Wysmolek, A., Stepniewski, R., Szkopek, T., Gaskell, P.E., Grüneis, A., Haberer, D., Bozek, R., Krupka, J. and Baranowski, J.M. (2011) Graphene Epitaxy by Chemical Vapor Deposition on SiC. Nano Letters, 11, 1786-1791. http://dx.doi.org/10.1021/nl200390e
[20]	Michon, A., Vézian, S., Ouerghi, A., Zielinski, M., Chassagne, T. and Portail, M. (2010) Direct Growth of Few-Layer Graphene on 6H-SiC and 3C-SiC/Si via Propane Chemical Vapor Deposition. Applied Physics Letters, 97, 171909. http://dx.doi.org/10.1063/1.3503972
[21]	Gale, J.D. (1997) Gulp: A Computer Program for the Symmetry-Adapted Simulation of Solids. Journal of the Chemical Society, Faraday Transactions, 93, 629-637. http://dx.doi.org/10.1039/a606455h
[22]	Materials Studio Ver.8.0 Including GULP, Dassault Systèmes BIOVIA.
[23]	Tersoff, J. (1988) New Empirical Approach for the Structure and Energy of Covalent Systems. Physical Review B, 37, 6991-7000. http://dx.doi.org/10.1103/PhysRevB.37.6991