On the Mechanical Analysis and Control for the Tension System of the Cylindrical Filament Winding ()
Received 10 March 2016; accepted 2 May 2016; published 5 May 2016

1. Introduction
The winding process consists of the production of mandrel and lining, the disposition of the glue solution, the filament drying, heat treatment, winding, solidification, testing, and reconditioning [1] . Among these processes, the tension control is a difficult significant process, which has a relatively huge impact on the performance of the winding product. The constant winding tension can make the filament arranged in order and the stress distribution between filament uniform, therefore it is beneficial for implementing the enhancement of the filament and increasing the workload of the composite winding product, otherwise it will result in more than 20 percent of the damage for the strength action of the filament. In terms of wet winding process, the control of tension can unify the results of the filament infiltration, reduce the thickness of the yarn sheet, and make the track of doffing accurate. Thus, the proper winding tension system and tension control is a significant element for achieving the quality winding product [2] .
Many domestic scholars conduct the theoretical analysis and experimental research for the filament winding tension. Ding Baogeng, Yang Fujiang et al. deduced the winding tension formula with full consideration for the prerequisite of the relaxation effect of the circle of winding glass fiber on the various layers. Xu Pingan established a new precise tension control system in his master’s thesis, controlling the tension of the yarns accurately during the filament winding process. Ren Qile designed and set up the tension control system in his doctoral dissertation, regarding the winding roller and swing rod as the object of study respectively. He employed the closed-loop control system of which the integral separation PID is the control strategy. Zhang Zongyi, Deng Guide, Shou Binan, and Li Xiaoyang et al. came up with an equivalent cooling method which made the pre- stress caused by the winding tension equivalent to the pre-stress caused by the cooling of the composite layer. They deduced the computational formula between the winding pre-stress and the cooling temperature of composite layer and utilized the general finite element software to study the influence of the winding tension on the stress of the round winding composite gas bottle based on the equivalent cooling method. Zhu Guohui et al. analyzed the wingding vessel of the low stress inner shell designing and deduced the winding original stress formula of the steel band winding. Jia Xiaoning et al. came up with a static friction microcomputer control system of application of power and tension, which uses the torque motor directly connected with the yarn group axis to exert the original tension and control the original tension in the microcomputer. T Ueki, S Suzuki, R Morikawa and, H Hashimoto describe optimization method of winding tension for preventing the wound roll defects under unstable environmental temperature based on the optimum design technique by Hashimoto [3] .
This paper conducts mechanical analysis for the unwinding roller during the cylindrical filament winding process. Based on the analyzed mechanical model, the control strategy of unwinding roller and winding process is deduced with the unwinding roller as the control target. This paper utilizes the dynamical-integral PID control strategy to achieve the control for the winding tension.
2. The Operating Principles of the Winding Tension Control System
The winding tension control system includes unwinding, tension acquisition, auxiliary facilities, and control, as is shown in Figure 1. Unwinding indicates the roller rotates to put lines under the tension of the winding filament. The filament moves with the rotating mandrel. Between the unwinding roller and the mandrel, many guiding roller control the direction of the winding filament to make it move steadily. The tension acquisition tests the tension in real time and transmits the results to the control part. In the open-loop control system, the winding roller radius is taken to test the tension with a relatively simple structure. While in the closed-loop control system, the force sensor is used to get the real-time tension and feed back the signal so as to achieve the closed-loop control. The auxiliary facility is based on the sensor’s features of fast response speed, high precision, and small displacement. The control indicates to calculate with the transmitted information in the testing part, have various control judgment, transmit the adjustment signal to the correspondent resistance production device, and finally achieve the goal to adjust the winding tension. The control part includes the controller and the executor of the tension control.
![]()
Figure 1. The composition of the general tension control system.
2.1. The Mechanical Analysis of the Winding Tension System
The winding tension control needs to ensure the effective performance of the winding products’ enhancement of the various layers of filament. However, the features of the winding filament, the winding radius change, the friction, the resin content will influence the stability of the tension during the winding process [4] .
The proper control of the filament winding tension can enhance the quality of the winding products effectively. The designed tension control system utilizes the closed-loop control method in this paper. The tension sensor feeds back the real-time tension and the system gives the control signal after calculation to drive the executive component to operate the AC servo motor to control the unwinding speed of the unwinding roller and finally the goal to control the tension is achieved. Utilize the operation of the motor to impose the torque resistance on the winding roller to control the feeding speed of the winding roller so as to achieve the goal of controlling the winding tension.
2.2. The Tension Analysis of the Unwinding Side
As is shown in Figure 1, the filament winding tension control system mainly achieves the tension control by controlling the unwinding speed of the unwinding roller. Therefore this paper firstly analyzes the force situation of the unwinding roller during the winding process. As is shown in Figure 2, the unwinding roller should meet the dynamic balance requirement during the winding process as is shown in formula (1).
The balance equation of the dynamic torque of the stressed unwinding roller is:
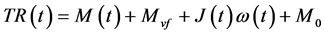 (1)
(1)
In the equation,
T: filament tension (N);
R(t): real-time radius of the yarn group (m);
M(t): resistance torque of the motor (N∙m);
Mvf: friction torque of viscidity (N∙m);
ω: the speed of the yarn group (rad/s);
J: the rotational inertia of the winding roller (kg∙m2);
M0: the friction torque of the dryness (N∙m).
From Equation (1), it can be known that the control target of the tension control system is a complex real-time system, including the radius of yarn group, the angular speed of the winding roller, and the rotational inertia of the unwinding roller, which change along with the time.
Therefore the above equation needs to be simplified, ignoring the elements which has less influence and has smaller change along with time. The detailed simplifying elements are analyzed as follows:
![]()
Figure 2. The force analysis of the winding roller.
1) The dryness and viscidity friction have little change along with time and have little influence on the system, thus they can be ignored;
2) The instant change has little influence on tension thus it can be ignored, such as the J(t)ω(t), which is the rotational inertia of the unwinding roller and the rotational inertia of filament.
3) Because the rotational inertia of the yarn group is a steady state value which does not change along with time, the rotational inertia of yarn group can be ignored.
According to the above principles, the Equation (1) can be simplified into:
 (2)
(2)
When the executive motor of the tension control system works normally, it usually is in a condition of dynamic braking. Its torque relationship is shown as Equation (3):
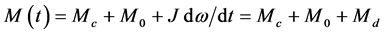 (3)
(3)
In the equation, M represents motor, the subscript c electromagnetic torque, 0 the no-load torque, d the dynamic torque; ω the angular speed.
Because there are few no-load motors during the winding process, the no-load torque M0 can be ignored; besides, when the motor is in a condition of steady rotation, its dynamic torque Md is 0. Therefore the Equation (3) can be simplified into Equation (4):
 (4)
(4)
Because,
 (5)
(5)
In the above equation, K is the electric constant of the motor; Φ is the main flux and Id is the torque current. And because:
 (6)
(6)
In the above equation, R is the radius of the yarn group; F is the tension.
Deduced from the above:
 (7)
(7)
Converse the Equation (7):
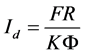 (8)
(8)
From the equation, it shows that the tension is related to the radius of the yarn group and the current component. To make the tension remain constant, the current Id should be controlled linearly according to the radius change of the yarn group. In other words, the control of the braking torque of the motor is achieved through the control of the motor current, and then the tension control is achieved also. From the Equation (8), it is shown that the torque component Id can be confirmed and the closed-loop control of tension can be achieved through testing and feeding back the radius of yarn group and the tension.
2.3. The Mechanical Analysis of the Tension Measuring Mechanism
The real-time tension acquisition is a significant feedback part in the tension control system. The proper periodical data acquisition for the real-time data of tension can enhance the control precision effectively. The popular tension acquisition method is shown as Figure 3. The three guide rollers are used to have tension measurement in the way of force transmission. The three guide rollers are arranged as the structure indicated in Figure 3. The tension sensor is set below the guide roller 2. When the mandrel rotates, the yarn will be winded and rotated around the mandrel. When the winding speed exceeds the unwinding speed, the yarn will have tension action. This tension will be transformed into the pressure action for the guide roller 2, be tested by the tension sensor and be fed back to the controller after getting the correspondent signal, thus constituting the feedback input of the closed-loop control. Such kind of means has simple structure, good application effect and it is easy to
![]()
Figure 3. The tension test of the three guide rollers.
implement.
The force analysis of the measuring device is indicated as Figure 4. When the middle guide roller 2 reaches a balance, its dynamic equilibrium is shown in Equation (9).
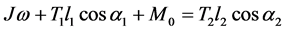 (9)
(9)
In the equation, J is the rotational inertia and ω is the angular speed of guide roller 2 respectively. M0 is the static friction torque of guide roller 2, l1 the filament length from guide roller 1 to guide roller 2, and l2 the filament length from guide roller 2 to guide roller 3. The static friction is ignored and the above equation can be simplified into:
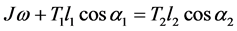 (10)
(10)
When the two sides of guide roller 2 have tension change resulting from the speed change, the positive pressure of guide roller 2 is calculated as Equation (11).
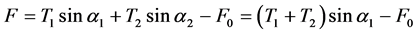 (11)
(11)
In this equation, F0 is the original pressure in the condition of balance, which is decided by the original winding tension.
2.4. The Analysis of Dynamic Compensation
During the winding process, because the non-uniform speed of winding the yarn resulting from the acceleration and deceleration motions, the tension finally changes. Therefore the control system cannot follow up and adjust in time and finally the filament is broken or loose. Thus, during the winding process, when the acceleration or deceleration motion caused by certain elements occurs, to ensure the uniform speed of winding the yarn, the speed compensation is required for unwinding roller. Normally certain braking torque will be imposed on the executive motor of the unwinding roller so that the tension can be maintained as constant. The dynamic torque is:
 (12)
(12)
In the above equation, J represents rotational inertia, p filament, m the roller.
During the filament winding process, the rotational inertia of filament is changing dynamically. It is in direct proportion to the radius change of the yarn. Therefore it can be calculated through Equation (13).
![]() (13)
(13)
In the equation, ρ is the density of the yarn; b is the width of yarn; R is the radius of yarn group.
Then,
![]() (14)
(14)
![]()
Figure 4. The force analysis of the measuring device.
The simultaneous equation is:
![]() (15)
(15)
As is shown in Equation (15), the dynamic torque Md which needs compensation can be calculated through tracking the radius of the unwinding and winding yarn group and the accelerated speed of the unwinding roller. So it shows that the unwinding roller needs to remain a constant linear speed for achieving the control of the winding filament’s constant tension.
3. The Tension Control of the Winding Filament
The filament winding tension takes the closed-loop control method [5] . The tension sensor feeds back the real-time tension and the system gives the control signal after calculation to drive the executive component to operate the AC servo motor to control the unwinding speed of the unwinding roller and finally the goal to control the tension is achieved. The control principle is shown as Figure 5.
The classic PID strategy is used broadly in various closed-loop control systems [6] . However, as for the non-linear complex system like filament winding tension control, the classic PID control has poor effects. The modified PID control strategy has high demand for calculation and controller, such as the PID control based on the neural network. Because this paper aims to have the tension control for the cylindrical winding product, the dynamic integral of PID can meet the demand for the calculation and non-linear change [7] .
The input of the dynamic integral PID controller changes the contained integral and differential parts of PID controller through weighting coefficient β and finally achieve the steady control of the system [8] .
When β = 0, the deviation e will exceeds the normal value. The PID controller uses the PD to control thus the system will have relatively fast responding speed and meanwhile it can be avoided to expand the overshoot.
When β = 1, the PID controller will use PI to control.
When 0 < β < 1, PID controller is controlled by the universal PID to ensure the control precision of system.
If the deviation time function is![]() , the deviation change rate time function is
, the deviation change rate time function is![]() , and the time of sampling is n, e(t) will disperse into e(n), r(t) will disperse into r(n), and
, and the time of sampling is n, e(t) will disperse into e(n), r(t) will disperse into r(n), and![]() . The dynamic integral PID control equation is shown as Equation (16).
. The dynamic integral PID control equation is shown as Equation (16).
![]() (16)
(16)
From Equation (5) to Equation (8): n is the number of sampling, n = 0, 1, 2; T is the period of sampling; u(n) is the output at the nth sampling; e(n) is the deviation signal; Kp is the proportion coefficient, KI is the integral coefficient, KD is the differential coefficient.
According to the adjustment principles for the various coefficients of PID during the filament winding process, when the deviation of system is great, the integral action should be weakened and when the deviation reduces, the integral action should be enhanced. The dynamic integral PID can weaken the system fluctuation occurs during the adjustment process to enhance the stability of system. The dynamic integral indicates that when the deviation is huge, the integral acceleration should slow down and the integral action should be weakened correspondingly; when the deviation is small, the integral accumulation should accelerate and the integral action
![]()
Figure 5. The tension control principle.
should be enhanced correspondingly.
Set the coefficient G(e(n)), which is the function of deviation e(n). When the deviation increases, G(e(n)) will decrease, otherwise, it will increase. If the variation range of the time deviation ![]() in steady state is [a, b], the chosen coefficient G(e(n)) is shown as Equation (17).
in steady state is [a, b], the chosen coefficient G(e(n)) is shown as Equation (17).
![]() (17)
(17)
The integral term of the dynamic integral PID is shown as Equation (18).
![]() (18)
(18)
As is shown in Equation (18), the interval of G(e(k)) is [0, 1]. When the deviation exceeds the expected value, make the coefficient ![]() and do not accumulate the current deviation; when
and do not accumulate the current deviation; when![]() ,
, ![]() , and the system normally is controlled by PID. At that time, the current e(n) will be accumulated and the coefficient of integral is shown as Equation (19).
, and the system normally is controlled by PID. At that time, the current e(n) will be accumulated and the coefficient of integral is shown as Equation (19).
![]() (19)
(19)
When![]() , the integral accumulates a part of the current value, the results vary in the interval of [0,e(n)], and the speed of integral varies in the interval of
, the integral accumulates a part of the current value, the results vary in the interval of [0,e(n)], and the speed of integral varies in the interval of
![]() .
.
Substitute Equation (18) to Equation (17) and the equation of the dynamic integral PID is shown as Equation (20).
![]() (20)
(20)
To test the dynamic integral PID control strategy, this paper chooses MatLab to have the simulation experiment. The step signal of 1 is chosen in the simulation. Its corresponding results show that the response and overshoot of the normal PID is shown in Figure 6. The duration of the shock cycle is longer. After about 15 seconds, the signal tends to be stable. The overshoot has reached 1.6 during the first 5 second. Obviously the dynamic integral PID is better than the normal PID (as is shown in Figure 7). The shock lasts less than 10 seconds. And the overshoot has reached 1.3. It indicates that the dynamic integral PID has better adjustment function for the overshoot, better steady-state performance, better adjustment quality, and better system transition. Therefore the dynamic integral PID control strategy has faster respond to the step and higher control precision, thus it is proper to be the filament winding tension control strategy.
![]()
Figure 6. The step of the classic PID parameter changes.
![]()
Figure 7. The step of the dynamic integral PID parameter changes.
4. Conclusion
To make the filament of the cylindrical winding product has constant tension and give full play to the fiber reinforced function, this paper analyzes the force on the unwinding roller and the tension acquisition part during the winding process, utilizes the motor to impose resistance torque on the unwinding roller during the process, designs and implements the tension closed-loop control system of which the unwinding roller is the control target. That system chooses dynamic integral PID control strategy. The simulation experiment results show that the response and overshoot of the normal PID obviously exceed those of dynamic integral PID. It indicates that the dynamic integral PID has better adjustment function for the overshoot, better steady-state performance, better adjustment quality, and better system transition. Therefore, the control system has relatively good stability, the overshoot is decreased efficiently, and the response time of system is shortened.