Solution of Linear Dynamical Systems Using Lucas Polynomials of the Second Kind ()
Received 23 February 2016; accepted 24 April 2016; published 27 April 2016

1. Introduction
Even in recent books (see e.g. [1] [2] ), the solution of linear dynamical systems, both in the discrete or continuous time case, is expressed by using all powers of the considered matrix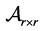 . As a consequence, if we want to write down explicitly the solution, it is necessary to construct the Jordan canonical form of
. As a consequence, if we want to write down explicitly the solution, it is necessary to construct the Jordan canonical form of 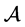 and, in the case of a defective matrix (i.e. if non trivial Jordan blocks appear in its canonical form), this implies cumbersome computations.
and, in the case of a defective matrix (i.e. if non trivial Jordan blocks appear in its canonical form), this implies cumbersome computations.
In order to avoid this serious problem, we propose here an alternative method, based on recursion, using the 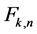 functions, which are essentially linked to Lucas polynomials of the second kind [3] (i.e. the basic solution of a homogeneous linear recurrence relation with constant coefficients [4] [5] ), and to the multi-variable Chebyshev polynomials [6] .
functions, which are essentially linked to Lucas polynomials of the second kind [3] (i.e. the basic solution of a homogeneous linear recurrence relation with constant coefficients [4] [5] ), and to the multi-variable Chebyshev polynomials [6] .
After recalling the 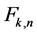 functions and their connections with matrix powers [7] , we can show, in Section 2, that the use of matrix powers and matrix function representations (see e.g. [7] [8] ) gives us the possibility to use only powers of the considered matrix up to (at most) the order
functions and their connections with matrix powers [7] , we can show, in Section 2, that the use of matrix powers and matrix function representations (see e.g. [7] [8] ) gives us the possibility to use only powers of the considered matrix up to (at most) the order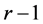 . This is a trivial consequence of the Cayley-Hamilton theorem, and should be used, in our opinion, to reduce the computational cost of solutions. Another shown possibility is the use of the Riesz-Fantappiè formula, by means of which the Taylor expansion of solution is completely avoided.
. This is a trivial consequence of the Cayley-Hamilton theorem, and should be used, in our opinion, to reduce the computational cost of solutions. Another shown possibility is the use of the Riesz-Fantappiè formula, by means of which the Taylor expansion of solution is completely avoided.
In Section 3, we prove our main results, relevant to an alternative method for the solution of linear dynamical systems, both in the discrete and continuous time case and via the Riesz-Fantappiè formula, also known in literature as the Dunford-Schwartz formula [9] , (but the priority of the first Authors is undubtable).
Some concrete examples of computation are presented in Section 4, showing the more simple complexity of our procedure with respect to the traditional algorithms, as they appear in the above mentioned books.
We want to remark explicitly that, in our article, by using the 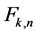 functions (essentially linked to Lucas polynomials of the second kind), our methodology builds a bridge, to our knowledge not previously well known, between the Theory of Matrices and that of Special Functions, which are usually considered as very different fields. Furthermore, the use of the Riesz-Fantappiè formula reduces to a finite computation the algorithms used in literature, making use of series expansions, and consequently dramatically improves the computation com- plexity of the considered problem.
functions (essentially linked to Lucas polynomials of the second kind), our methodology builds a bridge, to our knowledge not previously well known, between the Theory of Matrices and that of Special Functions, which are usually considered as very different fields. Furthermore, the use of the Riesz-Fantappiè formula reduces to a finite computation the algorithms used in literature, making use of series expansions, and consequently dramatically improves the computation com- plexity of the considered problem.
1.1. Recalling Fk,n Functions
Consider the 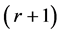 -terms homogeneous linear bilateral recurrence relation with (real or complex) constant (with respect to n) coefficients
-terms homogeneous linear bilateral recurrence relation with (real or complex) constant (with respect to n) coefficients 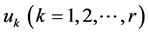 where
where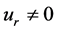 :
:
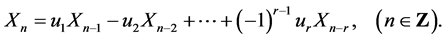 (1.1)
(1.1)
Supposing the coefficients vary, its solution is given by every bilateral sequence 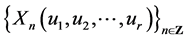 such
such
that 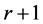 consecutive terms satisfy Equation (1.1).
consecutive terms satisfy Equation (1.1).
A basis for the r-dimensional vectorial space 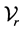 of solutions is given by the functions
of solutions is given by the functions 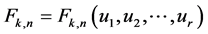 ,
, ![]() , defined by the initial conditions below:
, defined by the initial conditions below:
![]()
Since![]() , the
, the ![]() functions can be defined even if
functions can be defined even if![]() , by means of the positions:
, by means of the positions:
![]() (1.2)
(1.2)
Therefore, assuming the initial conditions ![]() the general solution of the recurrence (1.1),
the general solution of the recurrence (1.1), ![]() , is given by
, is given by
![]()
For further considerations, relevant to the classical method for solving the recurrence (1.1), see [5] .
An important result, originally stated by É Lucas [3] (in the particular case![]() ), is given by the equations
), is given by the equations
![]()
showing that all ![]() functions are expressed through the only bilateral sequence
functions are expressed through the only bilateral sequence![]() .
.
Therefore, we assume the following
Definition 1-The bilateral sequence![]() , solution of (1.1) corresponding to the initial conditions:
, solution of (1.1) corresponding to the initial conditions:
![]()
is called the fundamental solution of (1.1) (“fonction fondamentale” by É. Lucas [3] ), [4] .
For the connection with Chebyshev polynomials of the second kind in several variables, see [6] .
1.2. Matrix Powers Representation
In preceding articles [5] [7] , the following result is proved:
Theorem 1 Given an ![]() matrix
matrix![]() , putting by definition
, putting by definition![]() , and denoting by
, and denoting by
![]()
its characteristic polynomial (or possibly its minimal polynomial, if this is known), the matrix powers![]() , with integral exponent n, are given by the equation:
, with integral exponent n, are given by the equation:
![]() (1.3)
(1.3)
where the functions ![]() are defined in Section 1.1.
are defined in Section 1.1.
Moreover, if ![]() is not singular, i.e.
is not singular, i.e.![]() , Equation (1.3) still works for negative integers n, assuming the definition (1.2) for the
, Equation (1.3) still works for negative integers n, assuming the definition (1.2) for the ![]() functions.
functions.
It is worth to recall that the knowledge of eigenvalues is equivalent to that of invariants, since the second ones are the elementary symmetric functions of the first ones.
Remark 1 Note that, as a consequence of the above result, the higher powers of matrix ![]() are always expressible in terms of the lower ones (at most up to the dimension of
are always expressible in terms of the lower ones (at most up to the dimension of![]() ).
).
2. Matrix Functions Representation
It is well known that an analytic function f of a matrix![]() , i.e.
, i.e.![]() , is the matrix polynomial obtained from the scalar polynomial interpolating the function f on the eigenvalues of
, is the matrix polynomial obtained from the scalar polynomial interpolating the function f on the eigenvalues of ![]() (see e.g. the Gantmacher book [8] ), however, in many books (see e.g. [1] ), the series expansion
(see e.g. the Gantmacher book [8] ), however, in many books (see e.g. [1] ), the series expansion
![]() (2.1)
(2.1)
is assumed for defining (and computing)![]() . So, apparently, the series expansion for the exponential of a matrix is “hard to die”.
. So, apparently, the series expansion for the exponential of a matrix is “hard to die”.
Let ![]() the spectrum of
the spectrum of![]() . Denoting by
. Denoting by
![]()
the polynomial interpolating ![]() on
on![]() , i.e. such that:
, i.e. such that:![]() ,
,
![]() , then
, then
![]() (2.2)
(2.2)
If the eigenvalues are all distinct, ![]() coincides with the Lagrange interpolation polynomial and (2.2) is the Lagrange-Sylvester formula. In case of multiple eigenvalues,
coincides with the Lagrange interpolation polynomial and (2.2) is the Lagrange-Sylvester formula. In case of multiple eigenvalues, ![]() is the Hermite interpolation polynomial, and (2.2) reduces to Arthur Buchheim's formula, generalizing the preceding one.
is the Hermite interpolation polynomial, and (2.2) reduces to Arthur Buchheim's formula, generalizing the preceding one.
This avoids the use of higher powers of ![]() in the Taylor expansion (2.1). In any case, the possibility to write
in the Taylor expansion (2.1). In any case, the possibility to write![]() ,
, ![]() , in an easy block form, requires not only the knowledge of the spectrum, but even the Jordan canonical form of
, in an easy block form, requires not only the knowledge of the spectrum, but even the Jordan canonical form of![]() . It is necessary to compute the eigenvectors and moreover the principal vectors, if
. It is necessary to compute the eigenvectors and moreover the principal vectors, if ![]() is defective. A known machinery which implies a lot of computations.
is defective. A known machinery which implies a lot of computations.
The Riesz-Fantappiè Formula
A classical result is as follows:
Theorem 2 Under the hypotheses and definitions considered above, the resolvent matrix ![]() can be represented as
can be represented as
![]()
Then, by the Riesz-Fantappiè formula, we recover the classical result:
Theorem 3 If ![]() is a holomorphic function in the domain
is a holomorphic function in the domain ![]() and denoting by
and denoting by ![]() (with
(with![]() ) a closed set whose boundary is a piecewise simple Jordan contour
) a closed set whose boundary is a piecewise simple Jordan contour ![]() encompassing the spectrum
encompassing the spectrum ![]() of
of![]() , the matrix function
, the matrix function ![]() can be represented by:
can be represented by:
![]() (2.3)
(2.3)
In particular:
![]()
Remark 2 If the eigenvalues of![]() , are known, Equation (2.3), by the residue theorem, gives back the Lagrange-Sylvester representation. However, for computing the integrals appearing in Equation (2.3) it is sufficient the knowledge of a circle D, (
, are known, Equation (2.3), by the residue theorem, gives back the Lagrange-Sylvester representation. However, for computing the integrals appearing in Equation (2.3) it is sufficient the knowledge of a circle D, (![]() ), containing the spectrum of
), containing the spectrum of ![]() (by using the Gerschgorin theorem, and then knowing only the entries of
(by using the Gerschgorin theorem, and then knowing only the entries of![]() , without computing its eigenvalues). Therefore, this approach is computationally more convenient with respect to the Lagrange-Sylvester formula.
, without computing its eigenvalues). Therefore, this approach is computationally more convenient with respect to the Lagrange-Sylvester formula.
3. Solution of Linear Dynamical Systems Via Fk,n Functions
As a consequence of the above recalled results, we can prove our main results both in the discrete and continuous time case.
3.1. The Discrete Time Case
Theorem 4 Consider the dynamical problem for the homogeneous linear recurrence system
![]() (3.1)
(3.1)
where
![]()
Let
![]()
![]()
![]()
![]()
![]()
denote by ![]() the invariants of
the invariants of![]() , and recall the generalized Lucas polynomials
, and recall the generalized Lucas polynomials![]() ,
, ![]() , defined in Section 1.1.
, defined in Section 1.1.
Define the vector
![]()
and the matrix
![]()
then, the solution of problem (3.1) can be written
![]() (3.2)
(3.2)
That is, for the components:
![]()
Proof It is well known that the solution of problem (3.1) is given by
![]()
From the results about matrix powers, it follows that
![]()
Then, taking into account the above definitions of vectors ![]() and
and ![]() our result follows.
our result follows.
Remark 3 Note that, even if this is unrealistic, solution (3.2) still holds for negative values of n, assuming definition (1.2) for the ![]() functions when
functions when![]() .
.
3.2. The Continuous Time Case
Theorem 5 Consider the Cauchy problem for the homogeneous linear differential system
![]() (3.3)
(3.3)
where ![]() is the same matrix considered in the discrete time case.
is the same matrix considered in the discrete time case.
Let
![]()
![]()
![]()
![]()
![]()
denote by ![]() the invariants of
the invariants of![]() , and recall again the generalized Lucas polynomials
, and recall again the generalized Lucas polynomials![]() ,
,![]() .
.
Introduce the matrix ![]() and define the vector function
and define the vector function
![]()
then, the solution of problem (3.3) can be written
![]() (3.4)
(3.4)
Proof-It is well known that the solution of problem (3.3) is given by
![]() (3.5)
(3.5)
From the results about matrix exponential, it follows that
![]()
where
![]()
so that Equation (3.5) becomes
![]()
and taking into account the above positions, it follows
![]()
Then, Equation (3.4) immediately follows by introducing the vector function ![]() and the matrix
and the matrix ![]() defined above.
defined above.
Remark 4 Note that the convergence of the vectorial series in any compact set K of the space ![]() is guaranteed, as the components of
is guaranteed, as the components of ![]() are polynomials of weight not exceeding
are polynomials of weight not exceeding![]() , and consequently are bounded in K.
, and consequently are bounded in K.
3.3. The Continuous Case, Via the Riesz-Fantappiè Formula
By using the Riesz-Fantappiè it is possible to avoid series expansions. Indeed, we can prove the following result.
Theorem 6 The solution of the Cauchy problem (3.3) can be found in the form
![]()
where we denoted by![]() ,
, ![]() the invariants of
the invariants of ![]() and by
and by ![]() its characteristic polynomial.
its characteristic polynomial.
Proof It is a straightforward application of the Riesz-Fantappiè formula, taking into account the definition of![]() ,
,![]() .
.
4. Worked Examples
We show that the above results are easier with respect to the methods usually presented in literature ( [1] [2] ). Our technique is as follows: if the matrix ![]() has a low dimension (
has a low dimension (![]() ), its invariants can be computed directly by hand. If
), its invariants can be computed directly by hand. If ![]() it is more easy to compute the eigenvalues by using one of the classical numerical methods, and then the invariants are found as the elementary symmetric functions (with alternate sign) of the eigenvalues. This completely avoids the construction of the Jordan canonical form. No necessity to compute higher powers of matrix
it is more easy to compute the eigenvalues by using one of the classical numerical methods, and then the invariants are found as the elementary symmetric functions (with alternate sign) of the eigenvalues. This completely avoids the construction of the Jordan canonical form. No necessity to compute higher powers of matrix![]() .
.
4.1. Example 1 (Discrete Time Case)
We consider the ![]() system
system
![]() (4.1)
(4.1)
with matrix![]() :
:
![]()
The invariants of ![]() are by definition:
are by definition:
![]()
![]()
![]()
We will consider, the initial conditions:
![]() (4.2)
(4.2)
Then, as a consequence, we have:
![]()
and
![]()
Starting from the initial conditions:
![]() (4.3)
(4.3)
and by means of the recurrence relation
![]()
with ![]() and
and![]() , we find the following solution of the discrete dynamical system problem (4.1)-(4.2)
, we find the following solution of the discrete dynamical system problem (4.1)-(4.2)
![]() (4.4)
(4.4)
The (4.4) coincides with the following solution of the problem (4.1)-(4.2) obtained with the classical method of eigenvalues
![]()
![]()
![]()
4.2. Example 2 (Continuous Time Case)
We consider the ![]() system
system
![]() (4.5)
(4.5)
with matrix![]() :
:
![]()
The invariants of ![]() are by definition:
are by definition:
![]()
![]()
![]()
We will consider, the Cauchy problem with initial conditions:
![]() (4.6)
(4.6)
Then, as a consequence, we have:
![]()
and
![]()
Starting from the initial conditions (4.3) and by means of the recurrence relation
![]()
with ![]() and
and![]() , we find the following first values for the generalized Lucas polynomials
, we find the following first values for the generalized Lucas polynomials ![]() :
:
![]()
Here we compute an approximation of the solution of the Cauchy problem obtained by a suitable truncation of order N of the Taylor expansion
![]()
![]()
![]()
The exact solution of the Cauchy problem (4.5)-(4.6) is
![]()
![]()
![]()
such that we can compute, by using a Mathematica program, the approximation error obtained, for some values of N, in a fixed points t of the real axes. For example for ![]() and
and ![]() we obtain
we obtain
![]()
![]()
![]()
![]()
![]()
![]()
4.3. Example 3 (Continuous Time Case)
We consider the ![]() system
system
![]() (4.7)
(4.7)
with matrix![]() :
:
![]()
The invariants of ![]() are:
are:
![]()
![]()
![]()
![]()
We will consider, the Cauchy problem with initial conditions:
![]() (4.8)
(4.8)
Then, as a consequence, we have:
![]()
![]()
and
![]()
Starting from the initial conditions:
![]()
and by means of the recurrence relation
![]()
with ![]() and
and![]() , we find the following first values for the generalized Lucas polynomials
, we find the following first values for the generalized Lucas polynomials![]() :
:
![]()
Here we compute an approximation of the solution of the Cauchy problem obtained by a suitable truncation of the Taylor expansion
![]()
![]()
![]()
![]()
4.4. Example 4 (Using the Riesz-Fantappiè Formula)
Consider the problem
![]()
with matrix
![]()
Characteristic polynomial
![]()
Matrix eigenvalues
![]()
Matrix invariants
![]()
From the initial condition
![]()
we find
![]()
Riesz-Fantappiè formula
![]()
i.e.
![]()
![]()
Integrals computation (using the Residue Theorem).
![]()
![]()
Solution of the problem
![]()
i.e.
![]()
![]()
Checking our result
![]()
![]()
![]()
5. Conclusions
We have recalled that the exponential ![]() of a matrix
of a matrix ![]() can be written as a matrix polynomial, obtained from the scalar polynomial interpolating
can be written as a matrix polynomial, obtained from the scalar polynomial interpolating ![]() on the spectrum of
on the spectrum of![]() , and then avoiding the Taylor expansion for the exponential matrix.
, and then avoiding the Taylor expansion for the exponential matrix.
By using the functions![]() , and in particular the fundamental solution of a homogeneous linear recurrence relation, i.e. the generalized Lucas polynomials of the second kind, we have shown how to obtain the solution of vectorial dynamical problems, both in the discrete (3.1) and continuous (3.3) case, in terms of functions of the invariants of
, and in particular the fundamental solution of a homogeneous linear recurrence relation, i.e. the generalized Lucas polynomials of the second kind, we have shown how to obtain the solution of vectorial dynamical problems, both in the discrete (3.1) and continuous (3.3) case, in terms of functions of the invariants of![]() , instead of powers of
, instead of powers of![]() . These functions are independent of the Jordan canonical form of
. These functions are independent of the Jordan canonical form of![]() , and can be computed recursively, avoiding the knowledge of eigenvectors and principal vectors of the con- sidered matrices. Moreover, if the matrix is real, the
, and can be computed recursively, avoiding the knowledge of eigenvectors and principal vectors of the con- sidered matrices. Moreover, if the matrix is real, the ![]() functions are real as well, and complex eigenvalues do not affect the form of the solution.
functions are real as well, and complex eigenvalues do not affect the form of the solution.
Furthermore, the use of the Riesz-Fantappiè formula (Sections 3.3 and 4.4) reduces to a finite computation the algorithms used in literature.
Therefore, the methods considered in this article are more convenient, with respect to those usually found in literature, for solving linear dynamical systems.