Performance of the Heston’s Stochastic Volatility Model: A Study in Indian Index Options Market ()
Received 4 February 2016; accepted 3 April 2016; published 6 April 2016

1. Introduction
The time-varying volatility is considered one of the most cited stylised facts revealed by the traded financial assets. The property is well documented in the financial economics literature. The practitioners and academia have contributed in development of a variety of econometric models that account for this characteristic. Options pricing is no exception. These models have made their way to the options pricing as well in order to capture market dynamics more closely. Option pricing has been studied and debated in the academic world. At the same time, practitioners have brought in their advancements and improvements to pricing models best suited to their needs. These factors have led to the development of numerous option pricing models. The seminal work amongst these is that of Black and Scholes [1] . Many studies were conducted to test the performance of this model across the world. A few studies found results favouring the Black-Scholes (BS) model [2] - [6] . At the same time, another set of studies exists that reported against the model [7] - [10] . The chief amongst the criticisms of the model is the constant volatility assumption. Empirical evidence suggests that the volatility of an underlying is not constant.
As a result, new/modified models were proposed to overcome this assumption. A class of such models builds on the stochastic volatility framework. These models endeavour to relate volatility to a Cox-Ingersoll-Ross (CIR) process [11] - [17] . CIR is a square root process introduced by Cox et al. [18] . These models are computationally challenging. Amongst these models, the one proposed by Heston [11] remains very widely used as it offers a semi-closed form solution.
While these models have been studied in great detail in the developed markets, there are very few such studies in the developing markets. The number of similar studies in the Indian market is even less. Amongst such studies [19] - [22] , a vast majority of these made use of the closing data. The use of closing data subjects them to some serious issues/limitations, e.g., non-synchronous error.
Based on the literature reviewed, it appears that only a few studies have been conducted in the Indian market using high-frequency data. In this regard, Singh and Vipul [23] , in their analysis of a Two-Scale Realised Volatility (TSRV)-based BS, found that the BS model failed to capture the pricing dynamics of the Indian index options market. However, they documented that the TSRV-based estimates of volatility improved the performance of the BS model. Another study [24] on the BS model, using intraday data, confirmed the bias in the BS implied volatility (IV). However, a study on more mathematically sophisticated models such as the stochastic volatility model of Heston (SVH) using tick data is missing.
Given the literature gap mentioned above and in view of the fact that the CNX Nifty index options are the most liquid equity options in the world in terms of the number of contracts traded, it becomes imperative to conduct a comprehensive comparison of select option pricing models in this context. This study accomplishes it by performing an empirical analysis of the one-day-ahead out-of-sample performance of the SVH model. Further, we compare its performance to that of the TSRV-based BS model, using two years of tick data from the index options. Prices obtained by using these models are compared with the market prices of the options. Notably, the pricing errors are weighted with the respective liquidity of the options to compute the pricing errors for the entire index options market. The liquidity-weighted mispricing/pricing error is used to ascertain the best model for pricing the index options. The performance metrics are liquidity-weighted as options for some categories (e.g., in-the-money options) attract poor trading volumes. Using liquidity-weighted metrics would reduce any bias induced in the comparison due to liquidity issues. Additionally, to make the comparison robust, the performance of the models is evaluated across moneyness, maturity, and volatility of the underlying.
The remaining paper has been organised as follows: The details of the data and related issues are provided in Section 2. The formulation of the SVH model, the calibration approach, and the algorithms used are provided in Section 3. This section also includes the volatility calculation and the performance measures used for the comparison. Section 4 offers the results and discussions. The paper concludes with Section 5.
2. Data and Scope
Index options were introduced in India in June 2001. This study uses data from the CNX Nifty index options to examine and compare the performances of the two option pricing models, viz., a TSRV-based BS model and the SVH model. Tick data of two years (486 trading days), from 03 January 2011 to 31 December 2012, is used for the purpose of this study. The F&O segment, as well as the equity segment in India, trade during 9:15 a.m. to 3:30 p.m. from Monday to Friday, other than the designated holidays. The data for both segments are sourced from the NSE.
Below we provide the details of how the various inputs to the models were obtained:
Time to Expiration: Only trading days (instead of the calendar days) have been counted towards measuring the time-to-expiration [25] .
Risk-free rate: NSE provides the daily “zero-coupon yield curve” rates, based on the prices of the traded Treasury bills and bonds, on a weekly basis. In line with the approach followed by Vipul [26] and Singh and Vipul [23] , these rates are used as a proxy for the risk-free rate. For each day over the period of the study, the required risk-free rates for 7, 14, 21, 28, 35, 42, 49, 56 and 63 days are extracted from the data. Subsequently, each option is assigned a risk-free rate closest to its number of its days-to-maturity.
The BS model requires volatility of the underlying index to price options in addition to the other inputs. The details pertaining to the method and estimation of volatility are discussed in Section 3.
Data Screening
The following criteria are employed for data screening:
Options Data: Nifty index options with over 60 calendar days to maturity have poor liquidity (Figure A1 and Figure A2). Such options are therefore excluded from the study. Similarly, options with less than two days to maturity are removed as their prices may get distorted due to the expiration day effects [27] .
Non-synchronous Trading: To reduce the effect of non-synchronous trading, timestamp of transactions in the equity segment and the derivatives segment are matched (up to the second, hh:mm:ss).
Moneyness: Literature proposes several measures to calculate moneyness. In this study, the measure proposed by Bakshi et al. [28] , S/X, is used. In-the-money (ITM) options have this ratio greater than one for the call options, while out-of-the-money (OTM) options have this ratio as less than one. For the put options, the ratios are reversed. At-the-money (ATM) options, for both call and put, have the ratio equal to one.
Options which are far from the money lack sufficient liquidity, hence their price discovery may not be accurate. Such options are removed from the study and only options with moneyness range as 0.90 - 1.10 are considered [29] .
Based on the above-mentioned screening criteria, the number of options analysed in the study are 2290714 for calls and 2201306 for puts.
Equity Data: In addition to the options data, certain filtering criteria are employed to screen the data for Nifty spot prices as well. Transactions during sessions which do not reflect the normal market behaviour, like the pre- open session (9:00 a.m.-9:15 a.m.) and the special extended trading session (beyond 3:30 p.m.), are removed. Furthermore, Nifty being an index, its value changes whenever there is a transaction for any of its constituent stock(s). Since the tick data is recorded up to second and not beyond it, there are numerous cases of more than one value for a single timestamp. To remove any selection bias, all the values for a given timestamp are averaged. This average is taken as the index value for that timestamp.
3. Methodology
This section details the SVH model and the calibration methodology adopted. It also describes the procedure for TSRV calculation and the performance measures used for comparison of the pricing performance of the two models. The details of the BS model are not presented here.
3.1. Stochastic Volatility Model of Heston
Heston [11] proposed the first stochastic volatility model to have a semi-closed form solution. This is one of the main reasons for the popularity of the SVH model. It extends the BS model by accounting for its shortcomings like the non-normal distribution of the assets returns, the mean-reverting property of volatility and the leverage effect. The SVH model’s analytically tractable nature makes it preferred over similar models, despite its complexity. Attempts have been made to overcome other assumptions of the BS model, like the non-constant interest rate, and to add jumps to the return process. However, Bakshi et al. [28] concluded that adding jumps and stochastic interest rates, while increasing the complexity of the model, did not provide commensurate improvements.
There are two Brownian motions at work in a stochastic volatility model, one for the drift of the underlying price process and the other for its variance, unlike the BS model, where only the former is present. The SVH model follows the basic assumption of the stochastic volatility models that the variance of the underlying is a random variable. Also, it accounts for the asymmetric contribution of new information (a stylised fact in the financial markets) by assuming that the two stochastic processes are correlated.
The bivariate Ito’s lemma is used to derive the fundamental partial differential equations. The derivation follows the no-arbitrage argument, similar to that of the BS model. However, as opposed to the BS model, two derivative assets are required here to make the resulting portfolio risk-free, as there are two sources of randomness. The two derivative assets are on the same underlying, but differ in strike price and maturity. Because of the second Brownian motion, it is not possible to find a closed-form solution for the European options. Here, the SVH model has an advantage over other models in its category that it has a semi-closed form (or quasi-closed- form) solution available for the plain vanilla European options. This, in turn, makes it feasible to calibrate the model to market prices.
The model builds on the following partial differential equations (the time subscript has been dropped from spot price and variance for better readability):
 (1)
(1)
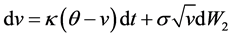 (2)
(2)
To take the leverage effect into account, the Wiener stochastic processes W1, W2 should be correlated 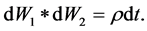
The quasi-closed form of the Heston model for a European option on a non-dividend paying stock is as follows:
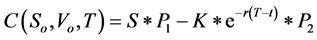 (3)
(3)
where,
 (4)
(4)
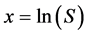 (5)
(5)
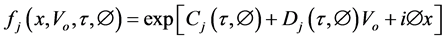 (6)
(6)
 (7)
(7)
 (8)
(8)
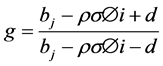 (9)
(9)
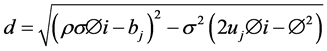 (10)
(10)
For j = 1, 2 we have
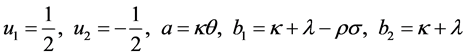
where,
S―Spot price; K―Strike Price; v―Variance; W1,2―Standard Brownian movements/Wiener processes; κ― Mean reversion rate; θ―Long run variance; σ―Volatility of variance; ρ―Correlation parameter; µ―Drift of the underlying; λ―Volatility risk; T―Maturity Date; τ-T-t (time remaining to maturity).
The model was implemented using the package “NMOF”, based on the work of Gilli et al. [30] , in the statistical tool R [31] . Since there is no direct solution available for the put options, its price is calculated using the put-call parity equation. Hence, for a given call option, the price of the put option on the same underlying, with the same strike and maturity, can be given by the below equation:
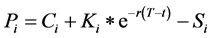 (11)
(11)
Due to the issues involved in the calculation of put option prices, studies of this nature generally concentrate on the call options for evaluating the performance of models, as the results of the put options are not a fair reflection on the performance of the model.
The SVH model does not have a closed form solution even for the call option. While some parameters of the model can be observed in the market (S, µ, K, T and τ), the other parameters need to be estimated. For this purpose, the model needs to be calibrated to the market price of the options. The calibration details, along with the algorithms considered for calibration, are provided in the next sub-section.
3.1.1. Calibration of the Model
Given the available market price of a European call option, we try to find parameters of a model such that the price of the option obtained from the model is very close to the market price of the option. This process is called calibration. Different algorithms are available depending on the requirements of the problem at hand. What is common in all calibration algorithms is that all such algorithms search a region of parameter space in their specific method, by trying to minimise the error between the market price and model price. So, while the accuracy is important, we also have to consider the time taken by an algorithm to converge. For this reason, global optimizers are usually not recommended as they are very slow. Particularly, this disadvantage becomes more prominent in studies like the present work, where a large amount of data is involved. The general approach involves box constraints; that is, applying upper and lower limits to all the parameters need to be calibrated. It also requires a good initial value as the starting point for the parameter vector.
Five parameters of the SVH model need to be estimated (κ, θ, σ, ρ and v0). The “inverse” method was adopted to estimate these parameters. It involves finding those parameters that produce the correct market prices of vanilla European options. To accomplish the same, an optimisation problem needs to be solved where the absolute differences between market prices and model prices of the vanilla European call options are minimised over the parameter space. We use the below equation for this minimisation procedure:
 2 (12)
2 (12)
where  denotes the price of the ith call option obtained using the parameters denoted by vector Ф,
denotes the price of the ith call option obtained using the parameters denoted by vector Ф, ![]() denotes the market price of the ith call option, and N is the number of options used for calibration on any given day. K and τ are the strike price and time to maturity for the ith option, and S is the spot price.
denotes the market price of the ith call option, and N is the number of options used for calibration on any given day. K and τ are the strike price and time to maturity for the ith option, and S is the spot price.
The choice of the optimisation algorithm to be used is discussed in the following subsection.
3.1.2. Choice of Optimisation Method
Ten optimisation algorithms were considered for this study. A ten day sample of the data was considered, and each algorithm was tested on the basis of accuracy and the execution time, to decide on the best algorithm. Due to time and resource constraints these algorithms could not be tested on the entire dataset. The following methods, used in this study, are implemented in R and have been modified as per the requirements:
(1) The two variants of the Differential Evolution (DE), a population based optimisation heuristic, proposed by Storn and Price [32] . (2) The Nelder-Mead algorithm [33] , which does not require derivatives of the objective function. (3) The BFGS algorithm, given by Broyden-Fletcher-Goldfarb-Shanno [34] ; it is known as the Variable Metric algorithm. It uses a Quasi-Newton method that does not require computing of the Hessian, instead uses an approximation for the same. (4) The nonlinear Conjugate Gradient method [35] , which is used to find the local minimum of a nonlinear function using only its gradient. (5) Simulated Annealing [36] , which can optimise nonlinear, discontinuous, as well as stochastic objective functions and can work with constraints. (6) The Limited Memory BFGS algorithm (L-BFGS-B), proposed by Byrd et al. [37] , is an extension of the BFGS; it approximates the Hessian.
Additionally, the two built-in R functions (namely, the “nlm” and the “nlminb”) were also considered. The “nlm”, proposed by Schnabel et al. [38] , uses Newton-like method for unconstrained problems which requires first derivatives. The “nlminb”, on the other hand, uses PORT routines, and was coded by David Gay in the Bell Labs PORT library collection [39] [40] . It is a reverse-communication Quasi-Newton method, which uses the trust-region approach. It is stable, efficient and does not depend too much on the initial input. It uses a gradient to solve unconstrained as well as box-constrained optimisation problems.
Based on the analysis detailed above, “nlminb” proved to be the best method for accuracy. Even though it was not the quickest method to converge (3rd out of the ten methods), it gave the best results in an acceptable timeframe. Hence, the subsequent analysis was conducted using this method.
The parameters of the SVH model have lower and upper bounds, beyond which the model is not defined. Despite the ability of “nlminb” to perform unconstrained optimisation, it is advisable to apply bounds to parameters, if available. This makes the convergence faster as the parameter space that an algorithm has to traverse, reduces. Hence, the lower and upper bounds were applied to the parameters.
The initial parameter vector (starting point) for the first day of the sample was obtained using a trial and error method. The model parameters were altered manually to minimise the “mean absolute error of the model price from the market prices”, and the vector thus obtained is used as the initial vector. For the subsequent days, the optimised parameter vector for day n is taken as the initial parameter vector for the day (n + 1). The assumption made here was the nature of the market would not change drastically over one day. Hence, the optimised parameters for the previous day can act as a good starting point for the current day.
The optimisation procedure results in parameter vectors Ф1, Ф2, ∙∙∙ Ф485, which give the best results for the minimisation equation for days 1 - 485 of the sample. The parameter vector of day n is then used to price options for the day (n + 1). For instance, Ф1 is used to price options on day 2, Ф2 on day 3, and so on. The call option prices obtained are subsequently used to calculate the prices of the corresponding put options using put-call parity. Liquidity-weighted performance measures are then calculated to ascertain the efficiency and consistency of the SVH model. The same is further used for comparison across the different pricing models. The performance measures are detailed in Section 3.3. The next subsection provides details of TSRV calculation.
3.2. Volatility Estimation Using TSRV
The issues related to the volatility calculated using closing prices are well documented. TSRV, proposed by Zhang et al. [41] , on the other hand is calculated using intraday data and is a much more efficient volatility estimate compared to estimate based on the closing prices. As the name suggests, it is estimated using two frequencies, a low frequency (typically five minutes) and a high frequency (typically one second). The former is primarily used for getting the estimate of the realised volatility, while the latter is used to remove the microstructure noise inherent in the price process. Singh and Vipul [23] provide more details of the estimation procedure and the issues involved with it.
The variance at the low frequency ![]() is estimated on the returns data of the index, sampled at every five minutes. And, returns corresponding to one-second interval are used to estimate the variance at the high frequency
is estimated on the returns data of the index, sampled at every five minutes. And, returns corresponding to one-second interval are used to estimate the variance at the high frequency![]() . The realised variance is estimated for any trading day (day t) using the TSRV formula as given below:
. The realised variance is estimated for any trading day (day t) using the TSRV formula as given below:
![]() (13)
(13)
where ![]() is the average number of returns across all the subsamples at the low frequency and N is the number of returns at high frequency for the day t.
is the average number of returns across all the subsamples at the low frequency and N is the number of returns at high frequency for the day t.
The TSRV estimator calculates the variance only for the trading hours, whereas most pricing models require the variance of the entire calendar day. Hence, the estimate obtained in the above equation is scaled up by the ratio of daily close-close to open-close historical variances. Below is the scaling factor that has been used in this study:
![]()
The same scaling factor has been used by Jacob and Vipul [42] , Koopman et al. [43] , and Martens et al. [44] . Following this, the close-close TSRV estimate is calculated as follows:
![]() (14)
(14)
This study attempts to test both the models ex-ante. Therefore, in the case of BS model, the sum of the close-close TSRV estimates for the previous n-days has been used as a proxy for the actual variance to be experienced by the market in the next n-days. The variance estimate is annualised assuming 252 days in a year, as the BS formula requires annualised volatility. This approach makes the implementation easier as the market participants do not have the benefit of hindsight, and using this method does not require to forecast the volatility for the remaining time-to-expiration.
Regularising the Series
In any time series of tick data, there may be missing values for certain timestamps due to no trading at those instances of time. For TSRV calculation in this study, the series is regularised such that all timestamps have a corresponding index value. For ticks with no transaction, the last available price is considered as a proxy for the current tick price.
3.3. Performance Measures
Liquidity-weighted performance measures are used to ascertain the one-day-ahead out-of-sample performance of the two option pricing models. It must be noted that the base is taken as the market price as it would ensure a fair comparison across different models by providing a common basis.
・ Liquidity-weighted Mean Percentage Error (MPE)
![]() (15)
(15)
・ Liquidity-weighted Mean Absolute Percentage Error (MAPE)
![]() (16)
(16)
where Ci and Ai are the calculated and actual prices of the ith option, respectively. Qi is the quantity traded for the ith option and N is the total number of options analysed.
The results and analysis of this comparison are presented in the next section.
4. Empirical Results and Discussion
The one-day-ahead out-of-sample analysis of the two models shows that the SVH model performs better than the BS model, both in terms of the frequency as well as the magnitude of the pricing errors (Table 1 and Table 2). We observe that the bias exhibited by the SVH model is less compared to that of the BS model, for both option types. While the BS model shows consistent overpricing with more than 90% call options as overpriced, the same figure for the SVH model is only 64.12%. For the put options, the SVH model also shows a consistent negative bias. Though, the same is still lower than that in the case of the BS model. It could be due to the error induced by the use of the put-call parity condition to arrive at the put prices, as the SVH does not provide the put prices directly.
The results provided in Table 1 are based on the frequency of mispricing. Hereafter, the study deals with the magnitude of mispricing, unless otherwise stated.
The overall results on the performance of both the models are provided in Table 2. The table contains three metrics, viz., the liquidity-weighted mean percentage error (MPE), the liquidity-weighted mean absolute percentage error (MAPE), and the liquidity-weighted standard deviation of the MPE (SD). The preliminary analysis indicated the presence of outliers in the data. The same were identified and removed. The results provided in Table 2 and the subsequent tables are based on the data trimmed at 5% level.
The results provided in Table 2 depict that the performance of the SVH model is superior to that of the BS model, with regard to both MAPE and MPE. The MAPE for the BS model is 48.15% and 62.07% for the call options and the put options, respectively. Notably, the same corresponding to the SVH model is 29.79% and 48.21%. The results of the MPE provide further evidence of the improvements shown by the SVH model over the BS model. However, prima-facie, the SD of the MPE indicates poor performance of the SVH model. In this regard, it is important to note that, in the first place, the SDs of the two models are not comparable. Additionally,
![]()
Table 1. Pricing bias exhibited by the select models.
Note: This table contains the bias shown by each model in terms of frequency of overpricing. The value in parenthesis shows the % of overpriced options in relation to total options contracts studied.
![]()
Table 2. Liquidity-weighted performance metrics for mispricing.
Note: This table provides the overall performance measures for the BS Model and the SVH Model. All the metrics considered are liquidity-weighted and are based on trimmed data. The total no. of options analysed are 2290714 and 2201306 for the calls and puts, respectively. This table also reports the significance of the difference between the mispricing of call and put options, tested using the Wilcoxon Rank-Sum test. For both the models, the alternate hypothesis tested is that mispricing in call options is lower than that of the put options. “****” denotes significance at α = 0.01%.
the lower (higher) SD in the case of the BS (SVH) model appears a result of the higher (lower) MPE and skewness of the pricing errors. It may be noted that the BS model produces one-sided bias (negative) for more than 90% of the cases; this leads to lower SD of the MPE.
Also, a statistical comparison of the mispricing magnitudes of both the models confirms that the SVH model outperforms the BS model comprehensively, for both option types. The results are provided in Table 3 and Table 4. The null hypothesis is rejected at 0.01% level of significance. It confirms that mispricing in the model 1 is statistically less than that in the model 2.
Further, for a robust comparison, the mispricing has been examined across different subgroups formed by moneyness, volatility and time-to-expiration of an option. It would enable us to identify whether the BS model performs poorly only for certain cases of volatility, moneyness, and time-to-expiration; or, it is inferior to the SVH model across the subgroups.
4.1. Mispricing Patterns across Moneyness
The performance across various moneyness groups is provided in Table 5 and Table 6. It may be noted that the results are presented in a way that conveys the meaning rather than the ratio of moneyness. It can be observed that the performance of the SVH model is far superior to that of the BS model, both in terms of MAPE and MPE. In the case of the BS model, the MAPE for the ATM call options is 27.20% vis-à-vis a considerably low MAPE of 12.72% for the SVH model. Similarly, for the ATM puts, the MAPE for the BS model and the SVH model are 35.12% and 21.27%, respectively. The results of the ATM subgroup and the other subgroups provide further proof that the SVH model is superior to the BS model.
The pattern across various subgroups is relevant once we establish that the mispricing in each subgroup is different from the remaining subgroups. To investigate this, the Kruskal-Wallis test (H-statistic) is used. This is a non-parametric test that compares the equality of medians for three or more subgroups. However, this test does not provide any information about the pair-wise differences. To overcome this, the Dunn’s test for the posthoc analysis was performed. The results validate that the subgroups indeed differ for both the option types, except for the ITM-deep ITM pair in the case of call options.
Table 5 and Table 6 demonstrate that both the models follow the same pattern for the MAPE and MPE. Both, MAPE and MPE reduce as options go from deep OTM to ITM. Similar patterns were documented by Bakshi et
![]()
Table 3. Comparison of models using Wilcoxon rank-sum test for call options.
![]()
Table 4. Comparison of models using Wilcoxon rank-sum test for put options.
Notes for Table 3 and Table 4: These tables provide the comparative performance of both the models, using Wilcoxon Rank-Sum test. The test is applied on absolute percentage error of the trimmed data. The alternate hypothesis states that the mispricing in model 1 is less than that of model 2. The values given in the table are the test statistic. The values in “()” give the p-values of the same. “****” denotes significance at α = 0.01%. This is a one-sided test; therefore, it become necessary to conduct a two-way comparison.
![]()
Table 5. Liquidity-weighted performance metrics for mispricing across moneyness for call options.
Note: This table provides the performance measures for all the models for various moneyness categories of NIFTY call options. All the metrics considered are liquidity-weighted metrics on the trimmed data. The moneyness range is taken from 0.90 - 1.10 with blocks of 0.04 points forming a group. For example, the “at-the-money” (ATM) range is 0.98 - 1.02.
![]()
Table 6. Liquidity-weighted performance metrics for mispricing across moneyness for put options.
Note: This table provides the performance measures for all the models for various moneyness categories of NIFTY put options. All the metrics considered are liquidity-weighted metrics on the trimmed data. The meaning of moneyness for calls and puts is reversed. The moneyness range is taken from 0.90 - 1.10 with blocks of 0.04 points forming a group. For example, the “at-the-money” (ATM) range is 0.98 - 1.02.
al. [28] for S&P 500 index options. Moreover, for the call options, even the SD follows the same pattern, though it deviates from the pattern slightly for the put options. The SVH model performs reasonably well for the ATM and ITM options, with lesser mispricing as well as increased consistency.
For the deep OTM options, the performance of both the models appears to be poor and unreliable. In this regard, two possible reasons can be proposed. Firstly, such options are very cheap compared to other options with different moneyness. This leads to a large percentage error even for a small pricing error as the base is very small. Secondly, owing to the high demand for the OTM options, the option writers seem to charge a premium for providing such options. Furthermore, even the SD for all models is very high in the case of the OTM options. It indicates that the results in the OTM category may not be very reliable, as the SVH and the BS do not appear to be equipped with required inputs to deal with such options.
4.2. Mispricing Patterns across Volatility
This section details the performance of the two models across four different subgroups based on the volatility of the underlying (TSRV-based estimates). The subgroups “0.05 - 0.10” and “0.20 - 0.25” refer to low and high volatility regimes, respectively. The remaining subgroups, viz., “0.10 - 0.15” and “0.15 - 0.20”, represent the normal market.
The Kruskal-Wallis test and the Dunn’s test for posthoc analysis were performed. The analysis shows that the subgroups formed based on the volatility subgroups are statistically different from each other, for both the models and the option types.
The analysis of the subgroups, presented in Table 7 and Table 8, reinforces the superiority of the SVH model over the BS model. This holds true for both MAPE and MPE, across option types. This is intuitive because the SVH model, being a stochastic volatility model, is expected to perform better on volatility changes, compared to a model based on constant volatility. The SVH model performs reasonably well for the call options in the normal volatility regimes, with the average MAPE and MPE for these around 23% and 10%, respectively. The performance of the BS model is poor, with the average MAPE and MPE being around 44% and 42%, respectively.
![]()
Table 7. Liquidity-weighted performance metrics for mispricing across volatility range for call options.
Note: This table provides the performance measures for all the models for various volatility subgroups of NIFTY call options. The volatility presented in the table is the annualised sum of the daily realised volatility of the underlying, scaled to close-close timeframe, for the days remaining to expiration. Volatility presented is in ratio form and can be converted to percent terms. All the metrics considered are liquidity-weighted metrics on the trimmed data.
![]()
Table 8. Liquidity-weighted performance metrics for mispricing across volatility range for put options.
Note: This table provides the performance measures for all the models for various volatility subgroups of NIFTY put options. The volatility presented in the table is the annualised sum of the daily realised volatility of the underlying, scaled to close-close timeframe, for the days remaining to expiration. Volatility presented is in ratio form and can be converted to percent terms. All the metrics considered are liquidity-weighted metrics on the trimmed data.
However, the models perform poorly when the volatility is either very high or very low. The volatility- risk-premium, charged by the option writers for options in the high volatility regime, may explain this behaviour. This premium overstates the market price of the options. Given the fact that none of the models are designed to account for such a premium, we observe large deviations from the market prices when the volatility is high.
Both models follow similar patterns for the call options. Further, the put options have the same pattern; though, it is different from the one observed for the call options. The similarity in the performances of the two models is surprising as both models have different theoretical foundations and also have different estimation methods.
4.3. Mispricing Patterns across Time-to-Expiration
Lastly, this section examines the behaviour of the mispricing with respect to the time-to-expiration of the options. For the purpose, the subgroups for this analysis are based on the calendar days. Therefore, the maturity of the option contracts covered in this study would translate to 2 - 60 days calendar days as we have ignored option with maturity less than two days to contain expiration effect. The data is divided into eight subgroups based on time-to-expiration.
Similar to the preceding subgroups, the Kruskal-Wallis test and the Dunn’s test for posthoc analysis were performed. These tests confirm that, for both models and option types, all subgroups are significantly different from each other.
As can be observed from Table 9 and Table 10, here again, the SVH model outperforms the BS model across all subgroups, for both MAPE and MPE. However, in the case of put options, the difference is not as large as in the case of the call options.
While there are no clear patterns, except the first subgroup (≤5 days), the SVH model gives a consistently good performance. In fact, the MPE for time-to-expiration of 31 days and more is close to just 3%. Although the liquidity is not very high for these subgroups, it is still enough to suggest that the SVH model can be used as a viable method for pricing the call options with larger maturities. A vast majority of the trades in the Indian options market takes place in the category of 6 - 30 days to maturity. Notably, in this region, the SVH model gives a reasonably good performance. Therefore, the SVH model seems to capture the pricing dynamics in the Indian index options market fairly well.
In sum, the findings from the preceding subsections confirm that the SVH model is a far better choice for pricing Indian index options, as compared to the BS model; it comprehensively outperforms the BS model for all subgroups, across option types. It gives a reasonably good performance independently as well. In totality, the SVH proves to be a better model for pricing the index options in the Indian context.
It may be noted that all the results presented here are without considering the transaction costs. However, the same would not have any implications when mispricing is compared across different models.
![]()
Table 9. Liquidity-weighted performance metrics for mispricing across time-to-expiration range for call options.
Note: This table provides the performance measures for all the models for various subgroups of NIFTY call options, based on time-to-expiration. The time-to-expiration range is based on calendar days. All the metrics considered are liquidity-weighted metrics on the trimmed data.
![]()
Table 10. Liquidity-weighted performance metrics for mispricing across time-to-expiration range for put options.
Note: This table provides the performance measures for all the models for various subgroups of NIFTY put options, based on time-to-expiration. The time-to-expiration range is based on calendar days. All the metrics considered are liquidity-weighted metrics on the trimmed data.
5. Summary and Conclusions
The SVH model seems to be a popular choice amongst academicians and practitioners alike. Despite that, there has been no study in India which analyses the performance of the model using tick data. This study tries to fill the gap by conducting a one-day-ahead out-of-sample performance analysis of the SVH model, and compares its performance to that of a TSRV-based BS model, using liquidity-weighted performance metrics.
The findings of this paper establish that the SVH model comprehensively outperforms the BS model, for both option types. Notably, the superior performance of the SVH model gets corroborated across moneyness/volatility/ time-to-expiration subgroups. Also, the statistical comparison among the models shows that the SVH model is a far better model for pricing Indian index options. Even the bias exhibited by the SVH model is significantly lower than that of the BS model.
Remarkably, the pattern followed by both the models appears to be the same across subgroups based on moneyness and volatility, especially for the call options. However, it appears to be a bit counter-intuitive as both models build on completely different theoretical foundations, and even their estimation procedures are not the same. For the moneyness subgroups, both models show that the mispricing reduces as an option goes from deep OTM to deep ITM. In the case of volatility subgroups, both models perform the best in the normal volatility regime.
Prima-facie, the SVH model appears to perform poorly compared to the BS model with regard to the SD of MPE, especially for the low volatility and the deep OTM subgroups. However, it is important to note that the large (small) SD of MPE is attributable to the small (large) MPE. In the case of the BS, the MPE is highly skewed; this leads to the small SD of MPE compared to that in the case of the SVH model. In sum, it may be concluded that the SVH model outperforms the BS model comprehensively. In other words, it captures the pricing dynamics of the Indian index options market fairly well.
Regarding its contribution, the study offers a significant extension to the existing empirical option pricing literature in India. It bridges an important gap on option pricing as no study has been conducted in the Indian options market on the Heston model, using tick data. This would help the trades and other stakeholders in the options market in identifying a suitable model to price and hedge their positions with higher accuracy.
Appendix
![]()
Figure A1. Average traded volume over time-to-expiration for the NIFTY call options.
![]()
Figure A2. Average traded volume over time-to-expiration for the NIFTY put options.
NOTES
![]()
*Corresponding author.
1As per a Futures Industry Association (FIA) study in 2014.
![]()
2The subscripts “i” and “t” have been dropped from K and T for clarity of presentation.