MHD Stagnation Point Flow of a Casson Fluid over a Nonlinearly Stretching Sheet with Viscous Dissipation ()
Received 6 February 2016; accepted 27 March 2016; published 30 March 2016

1. Introduction
The study of boundary layer flow over a stretching sheet has been a great challenge for researchers and it has immense applications in various industrial processes such as extraction of polymer sheet, paper production, wire drawing, glass-fiber production etc. The flow of incompressible fluid over a linearly stretching sheet was first investigated by Crane [1] . The Mass Transfer with suction or blowing over a stretching sheet was investigated by Gupta and Gupta [2] . The heat transfer over a stretching sheet of a hydromagnetic flow has been studied by Chakrabarthi and Gupta [3] . The flow over a stretching surface in three diemsional was discussed by Wang [4] . The MHD flow characteristics over a stretching sheet of a viscoelastic fluid was demonstrated by Andersson [5] . Later his work was extended by M. I. Char [6] with mass transfer.
The numerical analysis of magnetic field on Eyring-Powell fluid flow towards a stretching sheet has been discussed by N S Akbar [7] .
All the above investigations are restricted for the flow over a linearly stretching sheet but it is not necessary that the stretching sheet has to be linear. Vajravelu [8] analyzed the viscous flow over a nonlinearly stretching sheet. The heat transfer characteristics of a viscous fluid over a non linear stretching sheet was later introduced by Cortell [9] . A great number of studies for the boundary layer flow over a non linear stretching sheet under different aspects of heat and mass transfer, slip and convective boundary conditions etc., are presented in the literature [10] - [16] .
The study of stagnation point flow towards a stationary semi infinite wall was first introduced by Hiemenz [17] in a two dimensional case. In his work he reduced the Navier-Stokes equations into non linear ordinary differential equations with the help of similarity transformations. The same problem was extended by Homann [18] . Chiam [19] combined the works of Hiemenz and Crane i.e., the stagnation point flow towards a stretching sheet when the stretching rate of the plate is equal to the strain rate of the stagnation point flow and he found no boundary layer structure near the plate. El-Dab [20] obtained numerical solution of MHD flow of micropolar fluid with heat and mass transfer towards a stagnation point on a vertical plate.
In all these attempts, stagnation point flow due to the stretching sheet was analyzed. The boundary layer flow over a shrinking sheet was first investigated by Wang [21] . He dealt with stagnation point flow on a two dimensional shrinking sheet and axi symmetric stagnation point flow on a axisymmetric shrinking sheet. In contrast, Lok et al. [22] numerically studied non orthogonal stagnation point flow towards a stretching sheet. In his work, he determined that the obliqueness of a free stream line causes the shifting of the stagnation point towards the incoming flow.
Many fluids in industries resemble non-Newtonian behaviour. Non-Newtonian fluids are more appropriate than Newtonian fluids because of their varied industrial applications like petroleum drilling, polymer engineering, certain separation processes, food manufacturing etc.
For non-Newtonian fluids, the relationship between stress and the rate of strain is not linear and it is difficult to express all these properties in a single constitutive equation. Consequently, these fluid models [23] - [31] have been proposed depending on various physical characters.
Casson fluid is one such type of such non-Newtonian fluid, which behaves like an elastic solid, with a yield shear stress existing in the constitutive equation. This fluid model has its origin in modelling of flow of many biological fluids especially blood. Examples of such fluids include foams, yoghurt, molten chocolate, cosmetics, nail polish, tomato puree etc. Casson [32] introduced this model to predict the flow behaviour of pigment oil suspensions of the printing ink type. Later on, several researchers studied Casson fluid pertaining to different flow situations. The unsteady boundary layer flow and heat transfer of a Casson fluid over a moving flat plate with a parallel free stream was studied by Mustafa et al. [33] . The exact solution for boundary layer flow of Casson fluid over a permeable stretching/shrinking sheet with and without external magnetic field was discussed by Bhattacharyya et al. [34] [35] . The Casson fluid has an infinite viscosity at zero rate of shear and a yield stress below which no flow occurs and a zero velocity at an infinite shear rate [36] [37] . An excellent collection of articles can be found in [38] - [40] .
Motivated by the above investigations on non-Newtonian fluids and its wide applications, the objective of the present study is to analyze MHD stagnation point flow of a Casson fluid over a non linear stretching sheet with viscous dissipation. We have extended the works of Vajravelu [8] by considering magnetic field, stagnation point and viscous dissipation effects to the flow regime for more physical implications. In addition to this, the roles of the other parameters are explained in brief. The results are displayed in figures and tables. A parametric study of the physical parameters is conducted and a representative set of numerical results for the velocity and temperature profiles as well as the skin friction coefficient and local Nusselt number is illustrated graphically to show interesting features of the solutions. Here the governing partial differential equations were transformed into coupled non linear ordinary differential equations using appropriate similarity tranformations. The transformed ODE’s were then solved by Keller Box method. However, to the best of our knowledge no work has been carried out yet to analyze the present result. The layout of this paper is as follows.
In Section 2 the problem is formulated and similarity transformation has been employed to transform the partial differential equation into a non linear ordinary differential equations. In Section 3 a numerical solution using Keller box method has been discussed. In Section 4 the numerical results have been discussed graphically. Finally, the main concluding observations are mentioned in Section 5.
2. Mathematical Formulation
Consider the steady two-dimensional stagnation point flow of an incompressible Casson fluid located at y = 0. The flow being confined in the region y > 0. We take the non-linear stretching sheet in the XOY plane (see Figure 1). Along the x-axis, two equal and opposite forces are being applied. The surface is stretched in the x-di- rection such that the x-component of the velocity varies non-linearly along it, i.e.  where c > 0 is constant of proportionality and n is a power index. A magnetic field of uniform strength
where c > 0 is constant of proportionality and n is a power index. A magnetic field of uniform strength 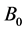 is applied perpendicular to the surface. The magnetic Reynolds number is taken to be small enough so that the induced magnetic field can be neglected in comparison to the applied magnetic field. It is also assumed that the ambient fluid is moved with a velocity
is applied perpendicular to the surface. The magnetic Reynolds number is taken to be small enough so that the induced magnetic field can be neglected in comparison to the applied magnetic field. It is also assumed that the ambient fluid is moved with a velocity , where a > 0 is a constant. The rheological equation of state for an isotropic and incompressible flow of the Casson fluid [Nakamura and Sawada [34] , Mustafa et al. [31] is given by
, where a > 0 is a constant. The rheological equation of state for an isotropic and incompressible flow of the Casson fluid [Nakamura and Sawada [34] , Mustafa et al. [31] is given by
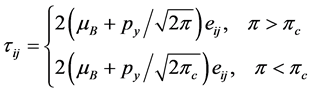
where  and
and 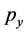 are the plastic dynamic viscosity, yield stress of the fluid respectively. Similarly
are the plastic dynamic viscosity, yield stress of the fluid respectively. Similarly 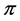 is the product of the component of deformation rate with itself,
is the product of the component of deformation rate with itself,  ,
,  is the (i, j)-th component of the deformation rate and
is the (i, j)-th component of the deformation rate and 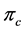 is a critical value of this product based on the non-Newtonian model.
is a critical value of this product based on the non-Newtonian model.
The continuity, momentum and energy equations governing the fluid flow are given by
![]()
![]()
![]()
where u, v are the velocity components in x, y direction respectively, 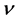 is the kinematic viscosity,
is the kinematic viscosity,  is the viscosity,
is the viscosity,![]() is the Casson fluid parameter,
is the Casson fluid parameter, ![]() is the thermal diffusivity of the fluid,
is the thermal diffusivity of the fluid, ![]() is thespecific heat and
is thespecific heat and ![]() is the magnetic field.
is the magnetic field.
The suitable boundary conditions are given by
![]()
Figure 1. Physical sketch of the given problem.
![]()
Here, c (![]() ) is the surface stretching sheet related parameter.
) is the surface stretching sheet related parameter. ![]() are the uniform temperature at the sheet, free stream temperature respectively and n is the power index related to the surface stretching speed.
are the uniform temperature at the sheet, free stream temperature respectively and n is the power index related to the surface stretching speed.
With the help of following similarity transformations
![]()
![]()
The Equations (1), (2) and (3) are transformed into coupled non linear ordinary differential equations as follows.
![]()
![]()
and the boundary conditions are transformed into
![]()
![]()
where ![]() is the Prandtl Number,
is the Prandtl Number, ![]() is the magnetic parameter,
is the magnetic parameter,
![]() is the Eckert number and
is the Eckert number and ![]() is the velocity ratio parameter.
is the velocity ratio parameter.
where prime denotes the differentiation with respect to![]() .
.
The quantities of practical interest are the Skin friction coefficient ![]() and the Local Nusselt number
and the Local Nusselt number ![]() which are defined as
which are defined as
![]()
where ![]() is the shear stress or skin friction along the stretching sheet and
is the shear stress or skin friction along the stretching sheet and ![]() is the heat flux from the sheet.
is the heat flux from the sheet.
Hence the dimensionless form of Skin friction ![]() and the Local Nusselt number
and the Local Nusselt number ![]() are given by
are given by
![]()
where ![]() is the local Reynolds number.
is the local Reynolds number.
3. Numerical Solution
The numerical solution for the above coupled ordinary differential equations for different values of governing parameters is obtained using finite difference scheme called Keller-box method. This method involves the four main steps which are as follows:
1) Reduce the equation or system of equations to a first order system.
2) Write the difference equations using central differences.
3) Linearize the resulting algebraic equations (if they are non-linear) by Newton’s method.
4) Write them in matrix-vector form and use the block-tridiagonal-elimination technique to solve the linear system.
This method has been widely used in laminar and turbulent boundary layer flows. It seems to be much faster, easier to program, more efficient and flexible to use than other methods.
4. Results and Discussion
The numerical computations are carried out with the help of Keller box method. The effects of different parameters like Stagnation point, MHD, viscous dissipation on velocity and temperature profiles has been clearly analyzed including with its physical quantities of significance. The effect of Casson fluid parameter on skin friction and local Nusselt number has been examined. Apart from those the various quantities of non linear stretching parameter were also analyzed.
To verify the accuracy of the present results, comparison has been made with the previous results of Vajravelu and Cortell (Table 1).
Table 1 clearly shows the values of skin friction coefficient ![]() and heat transfer rate
and heat transfer rate ![]() at the surface for different values of non linear stretching parameter n which are found to be in excellent agreement.
at the surface for different values of non linear stretching parameter n which are found to be in excellent agreement.
The effects of magnetic parameter M and velocity ratio parameter λ on the flow field velocity is displayed in Figure 2. It shows that the velocity of the fluid is not affected by various values of M for λ = 1 i.e., when the velocity of ambient fluid and the velocity of the sheet are same, where as for λ = 0.2 an increase in M decreases the velocity boundary layer thickness. However, with an increase in M the flow field velocity increases and boundary layer thickness decreases for λ = 2. Due to the Lorentz force induced by the action of magnetic field ,the thickness of boundary layer decreases for both λ = 0.2 and λ = 2.
![]()
Table 1. Values![]() ,
, ![]() of with Ec = 0, M = 0.
of with Ec = 0, M = 0.
![]()
Figure 2. Velocity profile for different values of M when λ = 0.2, 1, 2 and β = 2, n = 10, Pr = 0.71.
Figure 3 depicts the effect of the velocity ratio parameter on the flow field velocity. It can be observed that for λ < 1 i.e., when the stretching velocity of the sheet exceeds the free stream velocity, the velocity of the fluid and the boundary layer thickness increases with an increase in λ. Moreover, for λ > 1 i.e., when the free stream exceeds the stretching velocity, the flow velocity increases and the boundary layer thickness decreases with an increase in λ. If λ = 1 i.e., when the stretching and free stream velocities are equal, then there is no boundary layer of Casson fluid flow near the sheet.
Figure 4 and Figure 5 indicates the effect of Casson parameter β on velocity and temperature profiles for a non linear stretching parameter n = 10. It can be observed from Figure 4 that the fluid velocity decreases when β increases. Due to the increase of Casson parameter β, the yield stress ![]() reduces and hence the momentum boundary layer thickness decreases.
reduces and hence the momentum boundary layer thickness decreases.
![]()
Figure 3. Velocity profile for various values of λ when M = 1, β = 2, n = 10, Pr = 0.71 and Ec = 1.
![]()
Figure 4. Velocity profile for various values of β.
Figure 5 shows that the temperature decreases with increase in β implying that the thermal boundary layer decreases. In the vicinity of the sheet the temperature profile curves for larger values of β are lower than for those with smaller values of β. However, as we move far from the sheet within the thermal boundary layer, viscous dissipation vanishes and the curves for larger values of β tend to override for smaller values of β. Hence the temperature profiles intersect each other at a point and the behaviour goes other way round at this point.
Figure 6 and Figure 7 indicates the velocity and the temperature profiles for various values of nonlinear
![]()
Figure 5. Temperature profile for various values of β.
![]()
Figure 6. Velocity profile for various values of n.
![]()
Figure 7. Temperature profile for various values of n.
stretching parameter n. Figure 6 shows that the velocity of the fluid decreases with an increase in power index n, while the temperature increases (Figure 7). From the above two figures no specific variations were observed
when n is large. This is because of the term ![]() which approximately approaches to 2 when n reaches infin-
which approximately approaches to 2 when n reaches infin-
ity, as mentioned in the subfigures. Therefore the observations for the large values of n is not a study of interest.
Figure 8 indicates the effect of magnetic parameter M on velocity and temperature profiles. The velocity of the fluid decreases with an increase in M. This causes retarding effect on the flow field leading to the prominent reduction in velocity due to Lorentz force effect. Therefore, the Lorentz force increases the opposition of the flow of fluid reducing the velocity of the flow.
Figure 9 shows the temperature profile for various values of Pr. It is clear that the dimensionless parameter θ
![]()
Figure 8. Velocity profile for various values of M.
![]()
Figure 9. Temperature profile for various values of Pr.
decreases with the increase in Prandtl number. Since the Prandtl number is the ratio of momentum diffusivity to thermal diffusivity; it reduces the thermal boundary layer thickness. In general the Prandtl number is used in heat transfer problems to reduce the relative thickening of the momentum and the thermal boundary layers.
The influence of Eckert number Ec for linearly/non linearly stretching parameters i.e., n = 1, n = 10 is depicted in Figure 10. It illustrates that the temperature increases with an increase in Ec. The increase in temperature profile is higher for non linear stretching parameter than that for linear stretching parameter. The viscous dissipation produces heat due to drag between the fluid particles and this extra heat causes an increase of the initial fluid temperature, and these variations are clearly mentioned for linearly (n = 1) and nonlinearly stretching cases (n = 10). Both Figure 10 and Figure 11 reveal that the viscous dissipation may not only cause thermal reversal but also increase the thermal boundary layer whether ![]() or
or![]() .
.
![]()
Figure 10. Temperature profile for various values of Ec, λ = 0.2.
![]()
Figure 11. Temperature profile for various values of Ec, λ = 1.5.
Figure 12 and Figure 13 indicates the skin friction coefficient and Local Nusselt number with variations of Casson parameter β respectively. Figure 12 depicts the variation of the skin-friction coefficient with β for two values of non linear stretching parameter n = 1, n = 10. It is found that as β increases the skin-friction coefficient ![]() increases. From this figure, it can be observed that the shear stress at the wall is negative. Physically, a negative sign implies that a drag force has been exerted by the surface on the fluid, and a positive sign implies the opposite.
increases. From this figure, it can be observed that the shear stress at the wall is negative. Physically, a negative sign implies that a drag force has been exerted by the surface on the fluid, and a positive sign implies the opposite.
Figure 13 indicates the variation of heat transfer coefficient ![]() with Casson parameter β. As β increases, the heat transfer coefficient gradually increases. Wall temperature gradient
with Casson parameter β. As β increases, the heat transfer coefficient gradually increases. Wall temperature gradient ![]() decreases with increase in n.
decreases with increase in n.
![]()
Figure 12. Skin friction coefficient for various values of Casson parameter β.
![]()
Figure 13. Local Nusselt number for various values of Casson parameter β.
5. Conclusion
In the present study, MHD stagnation point flow of a Casson fluid over a non linearly stretching sheet are investigated with viscous dissipation. The numerical solution is obtained by Keller box technique. The effects of various governing parameters on heat flow characteristics were analyzed. Briefly the above discussion can be summarized as follows.
・ The velocity boundary layer thickness reduces for magnetic parameter M.
・ An increase in Casson parameter β decreases the velocity of the fluid as well as the thermal boundary layer thickness.
・ The velocity of the fluid decreases and temperature increases with an increase in nonlinear stretching parameter..
・ The Eckert number increases the thermal boundary layer thickness where as the Prandtl number decreases it.
・ Both the skin friction coefficient and heat transfer coefficient increases with Casson parameter β.