On the Relationship between the Pure Delay and the Natural Period of Oscillation ()
Received 12 February 2016; accepted 21 March 2016; published 24 March 2016

1. Introduction and Hypothesis
The approximate relationship
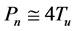 (1)
(1)
between the pure delay Tu and the natural period of oscillation Pn in industrial systems is well known to control engineers.
This relationship is in the core of the PID [1] tuning rules designed by Ziegler and Nichols [2] . If the values of integral times Ti in the methods of closed loop and open loop are equated, it comes down to
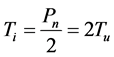 (2)
(2)
Solving the right side equation for Pn, (1) is reached. So, this relationship is widely used in practice to verify the identification of pure delay, which is not always easy to measure, and then calculate the parameters of PID controllers. However, it is remarkable that it has not received sufficient attention in academia.
This paper presents a demonstration of this relationship based on the behavior of first order systems with pure delay, using basic tools of linear control as root locus and polynomial algebra.
2. Proof
Since Pn = 1/fn, where fn is de oscillation frequency, and the angular natural frequency is wn = 2πfn, the natural period can be written as Pn = 2π/wn. Substituting this value in Equation (1), this becomes to
 (3)
(3)
Solving this equation for wn, an equivalent expression to Equation (1) is derived:
 (4)
(4)
Now, the most of industrial processes can be modeled by first order systems with pure delay, which have the Laplace transfer function [3]
 (5)
(5)
In this equation, Ke is the static gain and Tg the process time constant.
For the purpose of finding the characteristic equation of the system, the pure delay  can be represented by the second order Padé approximation [4] :
can be represented by the second order Padé approximation [4] :
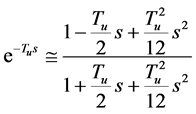 (6)
(6)
Then, G(s) is approximated as
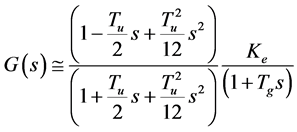 (7)
(7)
The characteristic equation of the system is obtained by adding numerator and denominator of Equation (7):
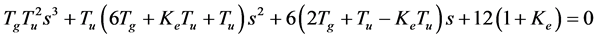 (8)
(8)
It is necessary to find the value of the static gain Ke where a pair of complex conjugate roots reaches the imaginary axis and the system becomes oscillatory with a natural frequency wn.
For readability, each coefficient of Equation (8) is identified as Ci. It is then
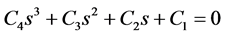 (9)
(9)
To be sure that the roots of this equation are in the left half-plane, a first requirement is that all coefficients are positive. In other words, a limit gain Ke can be found when any of these coefficients are set to zero. The only one who is able to accomplish this is C2:
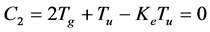 (10)
(10)
Solving for Ke, a first value Kel1 of a limit gain is then obtained:
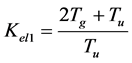 (11)
(11)
Now it must be determined if other values of Ke can produce imaginary roots in Equation (8). The Routh arrangement [5] of the characteristic equation is constructed for this purpose:
 (12)
(12)
As stated in Rooth-Hurwitz criterion [6] , the system poles are in the left half plane if there are no sign changes in the first column of the array, and the point where a root is located over the imaginary axis can be found by canceling any of its elements. The only element that is able to be null is the one for s1. Therefore, and considering that  is always positive, the condition can be written as
is always positive, the condition can be written as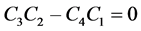 .
.
This corresponds to
![]() (13)
(13)
Solving this equation for Ke, there are two new values Kel2 wherein the real part of the roots is canceled:
![]() (14)
(14)
It is easy to show that Kel2a meets the condition of being positive and is also lower than the value of Kel1 given by Equation (11). Therefore Kel2a shall be the gain value that defines the point of oscillation of the system.
Then, to find the oscillation frequency of the system, Kel2a can be replaced into the characteristic Equation (8) and solving it for the values of s, which should be imaginary. However, this way the algebra becomes somewhat tangled. Therefore a property of polynomials is used, which states that secondary equations of the Routh arrangement (12) have roots that satisfy the characteristic equation. In particular, the auxiliary equation corresponding to s2 does not have odd powers, so it has symmetric roots with imaginary values:
![]() (15)
(15)
The roots of this equation are
![]() (16)
(16)
So the natural angular frequency wn is
![]() (17)
(17)
Now, in this equation the gain Ke must be replaced by the value Kel2a that brings the system to the oscillation, obtained in Equation (14). This leads to
![]() (18)
(18)
In most industrial systems the pure delay Tu is significantly lower than the time constant Tg, i.e.![]() . So Tu can be omitted when appears beside Tg in Equation (18). With this consideration, wn is expressed approximately as
. So Tu can be omitted when appears beside Tg in Equation (18). With this consideration, wn is expressed approximately as
![]() (19)
(19)
This value is almost coincident with the stated by Equation (4), which finally proof the hypothesis in Equation (1).