Experimental Study of the Water Absorption Kinetics of the Coconut Shells (Nucifera) of Cameroun ()
Received 5 January 2016; accepted 18 March 2016; published 21 March 2016

1. Introduction
The by-products of the coconut occupy an important place in the current research. This is justified by the dash of valorization of green energies and the fight against pollution. The shell of coconut (CS) is the subject of the research and several research tasks are devoted to it. Certain works are interested in the production of the activated carbon from CS. Other works deal with the use of the CS like charges in the composites [1] and also in concrete [2] . While certain works consider the use of the CS like stabilizer of the grounds [3] . Recent studies determined certain physicochemical and mechanics characteristics of this shell [4] . Its use in the composites implies the phenomena of diffusion of water. The kinetics of drying of the CS was the subject of a recent scientific study [5] , this work proposes to study the kinetics of absorption of CSs. Table 1 presents the nomenclature of the physical quantities used in the present work.
2. Materials and Methods
2.1. Materials
Coconut shells used in this study come from the areas of the South, the Littoral and the South-west of Cameroun. Two varieties of Shells are concerned, and are characterized by the form of their nut: a lengthened form (species 1) and a round form (species 2). Coconuts shells were separated from nuts and remained at the laboratory in approximate ambient moisture of 60% and at a temperature varying between 20˚C and 23˚C, for two months. The separation of coconuts shells from nuts was carried out mechanically and CSs was cleaned and cut in the form of the shape of a sphere in the southernmost direction (Figure 1(a)) to obtain samples (Figure 1(b)). For each one of these samples, we estimated, the rays interior noted Ri and outside noted Re, and the aperture θ while basing ourselves on geometrical layouts. For each species, 20 samples were produced for this study.
![]()
Table 1. Nomenclature of quantities.
![]()
Figure 1. Presentation of the two varieties of coconuts and the geometry of the samples.
2.2. Methods
The samples intended for the tests were dried in a standard drying oven of mark memmert model UN 160 to 105˚C for 4 hours. Under the above drying conditions after 4 hours, the mass of the samples of CS do not vary any longer. This was proven experimentally by [5] . After stoving the samples, once cooled, they were putting distilled water in order to follow their kinetics absorption. The experiments undertaken made it possible to determine the rate of water absorption and to model the kinetics of absorption of these shells using the gravimetric method. The experiment was carried with the help of numerical balance of 0.01 g precision. The samples are weighed after stoving before being immerged to determine their initial drying mass m0. For each sample, one notes the moment to which it was immerged, the sample was weighted aftertime duration in water. Making sure that the hygroscopy water was delicately removed and by minimizing the removing time from water. We note m(t) the wet mass of the sample at the instance t. We repeat this experiment until the mass of the sample does not vary anymore and it was notes the equilibrium mass meq.
2.3. Theoretic Considerations
2.3.1. Mathematical Model of the Phenomenon of Diffusion
The rate of absorption of water W compared to the dry matter of the samples is calculated starting from the drying mass m0 and of the equilibrium mass meq according to the formula (2). The instantaneous humidity content noted M(T) compared to the dry matter is calculated according to the formula (1). The ratio of the instantaneous rate of absorption which is the equivalent without dimension of the instantaneous water content is calculated according to the formula (3).
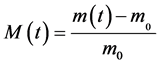 (1)
(1)
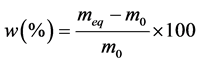 (2)
(2)
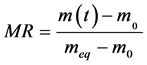 . (3)
. (3)
Table 2 presents the two mathematical models of the kinetic absorption of the vegetation products which were used to simulate those of CSs.
The software Matlab 2009 and Excel 2007 was used for the identification of the parameters of the various models. The effectiveness of a model is evaluated starting from the statistical criteria such as: the root mean square errors (RMSE) and the coefficient of correlation r2. In fact a model is better if r2 tends towards 1 for a lower value and with RMSE which tends towards 0 for a higher value. These parameters are expressed by the Equations ((4) and (5)) respectively.
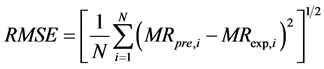 (4)
(4)
where 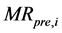 and
and 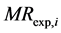 are the ratios of predicted and experimental rate of absorption respectively. N is the number of observations and P the number of constants.
are the ratios of predicted and experimental rate of absorption respectively. N is the number of observations and P the number of constants.
2.3.2. Estimation of the Effective Diffusivity
The Equation (5) is that of Ficks which governs the diffusion of mass through the vegetation products [14] .
![]()
Table 2. Mathematical models used in the kinetics absorption of CSs.
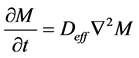 (5)
(5)
where Deff is the effective coefficient of diffusion in m2/s and M is the rate of absorption. The analytical solution of the Equation (5), for a radial diffusion in a hollow sphere (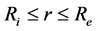 ) was developed by Carslaw and Jaeger in 1959 [14] . By admitting that the effective coefficient of diffusion depends neither on the concentration, nor on the position, the ratio of the instantaneous rate of absorption obeys the Equation (6).
) was developed by Carslaw and Jaeger in 1959 [14] . By admitting that the effective coefficient of diffusion depends neither on the concentration, nor on the position, the ratio of the instantaneous rate of absorption obeys the Equation (6).
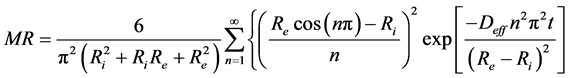 (6)
(6)
where MR is the moisture ratio of the water content of all the sample at the moment t and n is a positive entirety.
In the case that the interior radius r = Ri and the exterior radius r = Re are maintained with concentrations C1 and C2 respectively such as C1 = C2, the solution of Carslaw and Jaeger is given by the expression of the equation while limiting at the first term of this series we obtain Equation (7) given by;
 . (7)
. (7)
The Neperien logarithm of the Equation (7) by taking in account the two phases of absorption, gives the Equation (8) which makes it possible to determine the coefficients of diffusion Deff1 and Deff2 at the initial and final phases respectively. Where 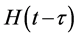 is the Heaviside function and τ is the duration of the initial phase of absorption.
is the Heaviside function and τ is the duration of the initial phase of absorption.
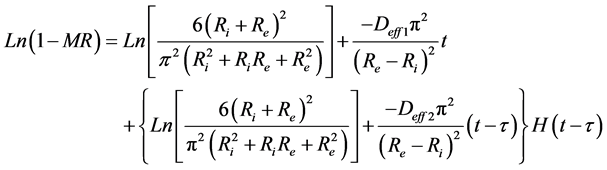 . (8)
. (8)
To determine the effective coefficient of diffusion, it is enough to trace the linear straight regression line of ![]() according to time t at the initial phase and at the final phase. The slope of this line makes it possible to calculate Deff according to Equation (9).
according to time t at the initial phase and at the final phase. The slope of this line makes it possible to calculate Deff according to Equation (9).
![]() . (9)
. (9)
3. Results and Discussion
3.1. Absorption Ratio
The instantaneous rates of absorption made it possible to plot the curves of the rate of absorption as a function of time. Figure 2 shows us the evolution of the rate of recovery according to time for the two species. It appears on this figure that the kinetics of absorption is faster at the beginning.
Table 3 gives the values of the rates of absorption obtained for each of the two species. It arises that species 2 has a little higher rate of absorption. It appears clearly in Table 3 that species 2 absorbs water a bit than species 1.
3.2. Kinetic of Water Absorption
To evaluate the kinetics of absorption of these Shells, starting from the experimental data, we calculate the moisture ratio of the instantaneous rate of absorption noted MR from Equation (3). The curve of MR for each species, presents two phases: an initial phase having a very great slope as of the first instance that the CS is in contact with water; and a final stage characterized by a very weak slope which is asymptotic with MR = 1. The
![]() (a)
(a)![]() (b)
(b)
Figure 2. Curves of the experimental points of absorption ratio of CSs. (a) Case of species 1; (b) Case of species 2.
durations of absorption of the two species are almost identical and equilibrium is reached at the end of 35 days of immersion.
To model this kinetics of absorption, we tested the models of Peleg, and Page.
3.3. Peleg Model
Equation (10) present the expression of the Peleg model:
![]() (10)
(10)
where k1 is the parameter which characterizes the kinetics of absorption as it can show in Equations (11) and (12).
![]()
Table 3. Values of the rate of absorption of the coconut shells.
![]() (11)
(11)
and
![]() (12)
(12)
k2 characterizes the rate of absorption indeed at equilibrium, when ![]() we obtain the Equation (13).
we obtain the Equation (13).
![]() . (13)
. (13)
The advantage of this model is that it can be put in the form of Equation (14):
![]() . (14)
. (14)
The exploitation of the Equation (14) makes it possible to obtain the values of the parameters k1 and k2 of Peleg, by linear regression. These statistical constants and these parameters are presented in Table 4. The mean values of the constants of Peleg enable us quantitatively to compare the kinetics of absorption of the two species. It arises from Table 4 that the values of the constants k1 and k2 are a bite different from one species to another since the confidence intervals overlap.
![]()
Table 4. Parameters values for Peleg model.
3.4. Page Model
The Page model is governed by the Equation (15).
![]() (15)
(15)
where a and n are the parameters which are obtained by a nonlinear regression using the software Matlab (2009). The statistical parameters and the values of the parameters of this model are given in Table 5.
The Page model predicts very well the kinetics absorption of the CS according to the values of the statistical parameters such as: r² and RMSE. Figure 3 shows the adjustment of Page and Peleg models to the experimental data of each species.
3.5. Coefficients of Effective Diffusivity
To determine the effective coefficients of diffusion, one takes into account the two phases of absorption kinetics. The Fick law expressed by Equation (7) was adopted for each phase. Equations ((16) and (17)) translate Fick law for the initial and final phases of the water absorption in this study.
![]() (16)
(16)
![]() . (17)
. (17)
![]()
Table 5. Values of the parameters and the statistical data of page model.
![]() (a)
(a)![]() (b)
(b)
Figure 3. Adjustment of the Page model on the experimental data. (a) Case of species 1; (b) Case of species 2.
![]()
Figure 4. Curves of Ln(1-Mr.) with respect to time for some samples.
where Deff1 and Deff2 indicate the coefficients of effective diffusivity at initial and final phases respectively.
Figure 4 shows the linear regression of experimental points of the species 1 and 2 at the initial phase. The slopes of those lines make it possible to calculate Deff1 at the initial phase. The same reasoning is used to determine the coefficients of diffusion of the final phase of the two species.
Table 6 gives the values of these coefficients for the two coconuts species. It is deduced from this table that the coefficients of diffusion of the two species for a given phase are a bite different.
Table 7 presents the comparison of the effective coefficients of diffusion during water absorption of the CS with some crops. The coefficients of diffusion of CSs at the initial phase are higher than those of a majority of the products except that of wood. According to the results of Table 7, the value of the coefficient of diffusion at the initial phase is close to that of grain of rice.
![]()
Table 6. Values of the coefficients of diffusion of the initial phase and the final phase.
![]()
Table 7. Comparison of the effective coefficients of diffusion during absorption.
4. Conclusion
The shells of two coconut species were separated from nuts and remained at the laboratory in approximate ambient moisture of 60% and at a temperature varying between 20˚C and 23˚C, for two months. Sample was obtained by cutting shells in portion of hollow sphere. Samples were dried in oven and immersed in the distilled water with an aim of studying their absorption kinetics. It was noted that at a temperature of 23˚C ± 1˚C, equilibrium content of balance is reached after a period of approximately 35 days in water. The rate of absorption of species 1 is 17.32% ± l.06% and that of species 2 is 20.42% ± 1.95%. The absorption kinetics of CSs presents two phases: an initial phase with great absorption kinetics in the first 28 minutes; and a final phase for the rest of time. It appeared clearly that the absorption kinetics of the two species is nearly identical. Of the 2 models tested (Peleg and Page), the Page models model very well the experimental data with a coefficient of correlation r2 > 0.98. The effective coefficients of diffusion obtained starting from the law of Fick: in the initial phase, they are (1.10 ± 0.23) × 10−10 m²/s and (1.04 ± 0.21) × 10−10 m²/s for species 1 and 2 respectively; in the final phase, they are (1.90 ± 0.35) × 10−12 m²/s and (2.08 ± 0.31) × 10−12 m²/s for species 1 and 2 respectively.
Acknowledgements
Thanks are due to the Head of the Civil Engineering Department of Fotso Victor University Institute of Technology for his help in various stages of the experimental work.
NOTES
![]()
*Corresponding author.