Statistical Mechanics for Weak Measurements and Quantum Inseparability ()
Received 22 January 2016; accepted 13 March 2016; published 16 March 2016

1. Introduction
Consider an M-particle Hilbert space, for pure states, the space can be decomposed as a tensor product of subspaces corresponding to each particle:
 (1)
(1)
where  is the total Hilbert space and
is the total Hilbert space and 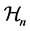 is the nth particle subspaces. Each particle subspace can be decomposed into N orthogonal subspaces (corresponding to the possible states a particle can take):
is the nth particle subspaces. Each particle subspace can be decomposed into N orthogonal subspaces (corresponding to the possible states a particle can take):
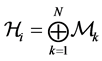 (2)
(2)
Combining both (1) and (2), we can write the total Hilbert space as:
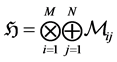 (3)
(3)
Such that the i runs for particles’, and j for the states. We now concentrate on two arbitrary particles labelled a, b in one state, assuming M > N, and separability of particles. We must have 2 particles―at least―occupying one state. However, separability assumption could be lost due to post-selection as we shall demonstrate below, and we could have a configuration with fuzzy occupation number per state. We may write the total Hilbert space in the following way:
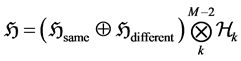 (4)
(4)
Then, we define the projection operator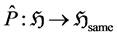 . This operator has suppressed indices for the pair of particles it measures whether the particles are in the same state, since the operator is symmetric under them, there is no need to mention them (particles are indistinguishable).
. This operator has suppressed indices for the pair of particles it measures whether the particles are in the same state, since the operator is symmetric under them, there is no need to mention them (particles are indistinguishable).
Let 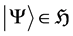 be a ray in the total Hilbert space, corresponding to the states of the quantum system.
be a ray in the total Hilbert space, corresponding to the states of the quantum system. 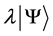 is also the same ray (belonging to the same equivalent class in
is also the same ray (belonging to the same equivalent class in ; where
; where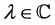 ) Hence one can construct a post- selected final state that one can―gently―measure, provided it belongs to the same equivalent class. If
) Hence one can construct a post- selected final state that one can―gently―measure, provided it belongs to the same equivalent class. If 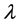 is selected to be some phase such that when a dual space of post-selection states, having
is selected to be some phase such that when a dual space of post-selection states, having 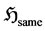 as its kernel:
as its kernel:
![]()
and,
![]()
Therefore, no two particles could be in the same state, given we - due to weak measurement- ended up in the state![]() . The factor
. The factor ![]() is calculated in [5] .
is calculated in [5] .
The emergence of quantum correlations between the particles in this system caused their occupation number to be fuzzy and undefined in the classical sense.
3. Microcanonical Ensemble for Weak Measurement
Inspired by the previous observation, we can look at it from a different perspective, this time using energy levels and bosons, similar argument can be made with fermions with slight modifications. We have M particles and N energy states, forming an ensemble. Starting from the Hilbert space of the ensemble![]() , it is usually decomposed as:
, it is usually decomposed as:
![]() (5)
(5)
Note that the index for the particles is not a label, just an index for numbering, as the particles are indistinguishable. But we are interested in a different decomposition, for our statistical analysis. We can decompose the Hilbert space as the sum of subspaces of configurations, i.e. the subspaces corresponding to the all possible distributions of particles on the energy levels. In this decomposition, we may right the state of the ensemble as:
![]() (6)
(6)
where, Ω is the number of possible (classical) ways to distribute energy levels to the particles and it is given by
![]() for bosons, and
for bosons, and![]() . The factors
. The factors ![]() are probability amplitude for each configu-
are probability amplitude for each configu-
ration, the kets ![]() resemble each configuration state; for example:
resemble each configuration state; for example:
![]() (7)
(7)
Notice in this decomposition, we do not have an assignment of energy for each particle, instead, we deal with occupation numbers and energy levels. Now, we need to specify the probability amplitudes for each configuration, this comes from the constraints that the ensemble must satisfy. Hence, they are determined by the properties of the ensemble and its surroundings. To keep the argument general, we shall not calculate them numerically, it is enough to know that are complex numbers and their square gives the probability of a configuration. Note also, that the system is ought to be in mixed state unless we assume the principle of equal probability a priori; witch is not acceptable as we have constraints on the system, for example the conservation of energy. Therefore the factors ![]() cannot be equal.
cannot be equal.
Now we calculate the microcanocical ensemble ![]() of the normalised state
of the normalised state ![]() from:
from:
![]() (8)
(8)
We notice the appearance of quantum interference terms![]() , this is a common observation in quantum mechanics, but not when dealing with statistical ensembles as we used to deal with sharp measurement and due to large numbers, and attaining the microcanocical ensemble by maximizing the number of ways with constraints, to get the most probable distribution. However, our argument is purely fundamental, and we could make the interference terms more prominent when post-selecting a state
, this is a common observation in quantum mechanics, but not when dealing with statistical ensembles as we used to deal with sharp measurement and due to large numbers, and attaining the microcanocical ensemble by maximizing the number of ways with constraints, to get the most probable distribution. However, our argument is purely fundamental, and we could make the interference terms more prominent when post-selecting a state![]() .
.
![]() (9)
(9)
like what we have discussed in Section 2 and calculating ![]() with respect to it:
with respect to it:
![]() (10)
(10)
The luxury of weak measurement allows post selection of the final state with slight different probability amplitudes such that the quantum interference terms do not vanish, hence having a general form of quantum pigeonhole principle for mixed/entangled states.
4. Entropy and Information
The density matrix of the ensemble ![]() is given by:
is given by:
![]() (11)
(11)
but assuming weak measurement, and a post selected state, we can write it as―showing quantum interference―
![]() (12)
(12)
The entropy is given by von Neumann formula:
![]() (13)
(13)
where ![]() is the density matrix of the ensemble under weak measurement. It is straightforward to show that the entropy of the ensemble under weak measurement is greater than the entropy under sharp one by the Schwartz inequality, indicating sort of quantum correlation between the particles. This is a direct consequence from the fuzziness and uncertainty about the occupation number for each energy level. Since the entropy for the distribution is the expected value for the information, information carried by the ensemble is more than the ensemble based on sharp measurement. In other words, quantum pigeons could carry multiple messages at the same time!
is the density matrix of the ensemble under weak measurement. It is straightforward to show that the entropy of the ensemble under weak measurement is greater than the entropy under sharp one by the Schwartz inequality, indicating sort of quantum correlation between the particles. This is a direct consequence from the fuzziness and uncertainty about the occupation number for each energy level. Since the entropy for the distribution is the expected value for the information, information carried by the ensemble is more than the ensemble based on sharp measurement. In other words, quantum pigeons could carry multiple messages at the same time!
Thus, quantum computers might be able to store more data in this way.
5. Thermal States
If the ensemble was immersed in a reservoir, the provability amplitudes are determined by the temperature of the heat bath, instead of writing each probability of the configuration separately―which is a formidable task. We can write the partition function in the following way:
![]() (14)
(14)
The probabilities were factored out as the term![]() , and we are only left with the degeneracy Ω, like the
, and we are only left with the degeneracy Ω, like the
standard statistical mechanics, plus the term ![]() resembling the interferences. Where
resembling the interferences. Where ![]() are the cosines
are the cosines
of the angles in the complex plane between the ![]() and
and![]() . Note that the round parentheses around the indices denote symmetrisation. Following the same steps, we can write the grand canonical partition function, where the probabilities are absorbed in
. Note that the round parentheses around the indices denote symmetrisation. Following the same steps, we can write the grand canonical partition function, where the probabilities are absorbed in![]() :
:
![]() (15)
(15)
Then we may write a distribution functions, but we notice in the quasi-continuum energy limit, the quantum interference terms become very small and we are left with Fermi-Dirac or Bose-Einstein statistics.
Therefore, the pigeonhole principle is ultra-quantum phenomenon and only matters when weak measurement is strictly preformed on an ensemble of few particles.
6. Discussion
We observe that we can construct the quantum pigeonhole principle for counting by a proper decomposition of the Hilbert space for the system of study, and by also using the right operator, or in logical sense, asking the right question. The necessity of measurement to be weak is apparent from the operator used and the freedom left for post-selecting the final state, as weak measurement only perturb the quantum system slightly. The conclusion was there are no two particles in one box, but that does not imply that there is one particle in each box. The latter statement comes from sharp measurement that assigns a definite state for a particle. We can reproduce the quantum pigeonhole effect for energy levels from the using the same argument in Section 2 on the decomposition of (5), and thereby have no two particles have the same energy. This fuzzy energy the ensemble of (5) seems really interesting for quantum logic and computing. Somehow, we let the ensemble carry more information that it would usually do in the case of sharp measurement. The post-selected state for the ensemble shows clearly how we gain a fuzzy notion of occupation number, no constraint on the system violated, energy remains conserved, and the number of particles remains the same. Nevertheless we no longer are able to specify the energy state for each particle, as they are no longer separate and in some form of correlation. This can be applied to any state, not just for energies. We mentioned energies because they are of an interest for statistical mechanics study. As what was done in Section 5 when the ensemble was immersed in a reservoir, or even in an open system. As long as the number of particles and energy levels is limited and no sharp measurement is preformed we still can notice the quantum pigeonhole effect. This effect shows that a particle can carry more than one energy value, therefore the ensemble can be made to carry more information than its standard capacity; when we don’t assign each particle with a specific energy. This could show usefulness in quantum computing. For example, a weak measurement could be a slight shift in energy levels in the post-selected state, by changing the properties of the well enclosing the ensemble increasing the capacity of information processing or storage by creating quantum correlations as seen above. However, this effect could only hold when the system has discrete states, in energy bands forming from very large ensembles, this effect no longer exists, as we have almost continuous energies in the ensemble.
7. Conclusion Remarks
With an ensemble composed of few quantum particles, a new quantum effect can be observed. Provided we only gently measure the system (i.e. avoid assigning each particle a single state; by sharp measurement), quantum interference allows extra configurations (extra ways) to arrange the ensemble. Particles loose separability and we get a different counting logic, giving rise to the quantum pigeonhole principle. This is a new insight to the quantum world, supporting Copenhagen interpretation. This new statistical mechanics could be of an interest in quantum computing and information theory. This effect could only be considered when the ensemble is not very large, as the effect is ultra-quantum, and appears when the energy states are very distinct, not―for example― when energy bands form.