A Regularized Newton Method with Correction for Unconstrained Convex Optimization ()
Received 17 January 2016; accepted 12 March 2016; published 15 March 2016

1. Introduction
We consider the unconstrained optimization problem [1] -[3]
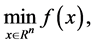 (1.1)
(1.1)
where 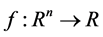 is twice continuously differentiable, whose gradient
is twice continuously differentiable, whose gradient 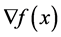 and Hessian
and Hessian 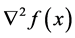 are denoted by
are denoted by 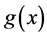 and
and 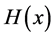 respectively. Throughout this paper, we assume that the solution set of (1.1) is nonempty and denoted by X, and in all cases
respectively. Throughout this paper, we assume that the solution set of (1.1) is nonempty and denoted by X, and in all cases  refers to the 2-norm.
refers to the 2-norm.
It is well known that 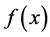 is convex if and only if
is convex if and only if 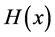 is symmetric positive semidefinite for all
is symmetric positive semidefinite for all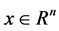 . Moreover, if
. Moreover, if 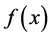 is convex, then
is convex, then 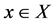 if and only if x is a solution of the system of nonlinear equations
if and only if x is a solution of the system of nonlinear equations
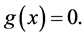 (1.2)
(1.2)
Hence, we could get the minimizer of  by solving (1.2) [4] -[8] . The Newton method is one of efficient solution methods. At every iteration, it computes the trial step
by solving (1.2) [4] -[8] . The Newton method is one of efficient solution methods. At every iteration, it computes the trial step
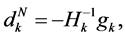 (1.3)
(1.3)
where ![]() and
and![]() . As we know, if
. As we know, if ![]() is Lipschitz continuous and nonsingular at the solution, then the Newton method has quadratic convergence. However, this method has an obvious disadvantage when the
is Lipschitz continuous and nonsingular at the solution, then the Newton method has quadratic convergence. However, this method has an obvious disadvantage when the ![]() is singular or near singular. In this case, we may compute the Moore-Penrose step [7]
is singular or near singular. In this case, we may compute the Moore-Penrose step [7] ![]() . But the computation of the singular value decomposition to obtain
. But the computation of the singular value decomposition to obtain ![]() is sometimes prohibitive. Hence, computing a direction that is close to
is sometimes prohibitive. Hence, computing a direction that is close to ![]() may be a good idea.
may be a good idea.
To overcome the difficulty caused by the possible singularity of![]() , [9] proposed a regularized Newton method, where the trial step is the solution of the linear equations
, [9] proposed a regularized Newton method, where the trial step is the solution of the linear equations
![]() (1.4)
(1.4)
where I is the identity matrix. ![]() is a positive parameter which is updated from iteration to iteration.
is a positive parameter which is updated from iteration to iteration.
Now we need to consider another question, “how to choose the regularized parameter![]() ?” Yamashita and
?” Yamashita and
Fukushima [10] chose ![]() and showed that the regularized Newton method has quadratic convergence under the local error bound condition which is weaker than nonsingularity. Fan and Yuan [11] took
and showed that the regularized Newton method has quadratic convergence under the local error bound condition which is weaker than nonsingularity. Fan and Yuan [11] took ![]()
with ![]() and showed that the Levenberg-Marqulardt method preserves the quadratic convergence. Numerial results ([12] [13] ) show that the choice of
and showed that the Levenberg-Marqulardt method preserves the quadratic convergence. Numerial results ([12] [13] ) show that the choice of ![]() performs more stable and preferable.
performs more stable and preferable.
Inspired by the regularized Newton method [13] with correction for nonlinear equations, we propose a modified regularized Newton method in this paper. At every iteration, the modified regularized Newton method first solves the linear equations
![]() (1.5)
(1.5)
to obtain the Newton step![]() , where
, where ![]() is updated from iteration to iteration, and solves the linear equations
is updated from iteration to iteration, and solves the linear equations
![]() (1.6)
(1.6)
to obtain the approximate Newton step![]() .
.
It is easy to see
![]() (1.7)
(1.7)
Then it solves the linear equations
![]() (1.8)
(1.8)
to obtain the approximate Newton step![]() .
.
The aim of this paper is to study the convergence properties of the above modified regularized Newton method and do a numerical experiment to test its efficiency.
The paper is organized as follows. In Section 2, we present a new regularized Newton algorithm with correction by trust region technique, and then prove the global convergence of the new algorithm under some suitable conditions. In Section 3, we test the regularized Newton algorithm with correction and compared it with a regularized Newton method. Finally, we conclude the paper in Section 4.
2. The Algorithm and Its Global Convergence
In this section, we first present the new modified regularized Newton algorithm by using trust region technique, then prove the global convergence. First, we give the modified regularized Newton algorithm.
Let ![]() and
and ![]() be given by (1.6) and (1.8), respectively. Since the matrix
be given by (1.6) and (1.8), respectively. Since the matrix ![]() is symmetric and positive definite,
is symmetric and positive definite, ![]() is a descent direction of
is a descent direction of ![]() at
at![]() , however
, however ![]() may not be. Hence we prefer to use a trust region technique.
may not be. Hence we prefer to use a trust region technique.
Define the actual reduction of ![]() at the kth iteration as
at the kth iteration as
![]() (2.1)
(2.1)
Note that the regularization step ![]() is the minimizer of the convex minimization problem
is the minimizer of the convex minimization problem
![]()
If we let
![]()
then it can be proved [4] that ![]() is also a solution of the trust region problem
is also a solution of the trust region problem
![]()
By the famous result given by Powell in [14] , we know that
![]() (2.2)
(2.2)
By some simple calculations, we deduce from (1.7) that
![]()
so, we have
![]() (2.3)
(2.3)
Similar to![]() ,
, ![]() is not only the minimizer of the problem
is not only the minimizer of the problem
![]()
but also a solution to the trust region problem
![]()
where![]() . Therefore we also have
. Therefore we also have
![]() (2.4)
(2.4)
Based on the inequalities (2.2), (2.3) and (2.4), it is reasonable for us to define the new predicted reduction as
![]() (2.5)
(2.5)
which satisfies
![]() (2.6)
(2.6)
The ratio of the actual reduction to the predicted reduction
![]() (2.7)
(2.7)
plays a key role in deciding whether to accept the trial step and how to adjust the regularized parameter.
The regularized Newton algorithm with correction for unconstrained convex optimization problems is stated as follows.
Algorithm 2.1
Step 1. Given![]() ,
, ![]() ,
, ![]() ,
,![]() . Set
. Set![]() .
.
Step 2. If![]() , then stop.
, then stop.
Step 3. Compute![]() .
.
Solve
![]() (2.8)
(2.8)
to obtain![]() .
.
Solve
![]() (2.9)
(2.9)
to obtain ![]() and set
and set
![]()
Solve
![]() (2.10)
(2.10)
to obtain ![]() and set
and set
![]()
Step 4. Compute![]() . Set
. Set
![]() (2.11)
(2.11)
Step 5. Choose ![]() as
as
![]() (2.12)
(2.12)
Set ![]() and go step 2.
and go step 2.
Before discussing the global convergence of the algorithm above, we make the following assumption.
Assumption 2.1. ![]() and
and ![]() are both Lipschitz continuous, that is, there exists a constant
are both Lipschitz continuous, that is, there exists a constant![]() ,
, ![]() such that
such that
![]() (2.13)
(2.13)
and
![]() (2.14)
(2.14)
It follows from (2.14) that
![]() (2.15)
(2.15)
The following lemma given below shows the relationship between the positive semidefinite matrix and symmetric positive semidefinite matrix.
Lemma 2.1. A real-valued matrix A is positive semidefinite if and only if ![]() is positive semidefinite.
is positive semidefinite.
Proof. See [4] . ♢
Next, we give the bounds of a positive definite matrix and its inverse.
Lemma 2.2. Suppose A is positive semidefinite. Then,
![]()
and
![]()
hold for any![]() .
.
Proof. See [13] . ♢
Theorem 2.1. Under the conditions of Assumption 2.1, if f is bounded below, then Algorithm 2.1 terminates in finite iterations or satisfies
![]() (2.16)
(2.16)
Proof. We prove by contradiction. If the theorem is not true, then there exists a positive ![]() and an integer
and an integer ![]() such that
such that
![]() (2.17)
(2.17)
Without loss of generality, we can suppose![]() . Set
. Set![]() . Then
. Then
![]()
Now we will analysis in two cases whether T is finite or not.
Case (1): T is finite. Then there exists an integer ![]() such that
such that
![]()
By (2.11), we have
![]()
Therefore by (2.12) and (2.17), we deduce
![]() (2.18)
(2.18)
Since![]() ,
, ![]() , we get from (2.8) and (2.18) that
, we get from (2.8) and (2.18) that
![]() (2.19)
(2.19)
Duo to (1.7), we get
![]()
From (2.10), we obtain
![]() (2.20)
(2.20)
where ![]() is a positive constant.
is a positive constant.
It follows from (2.1) and (2.5) that
![]() (2.21)
(2.21)
Moreover, from (2.6), (2.17), (2.13) and (2.19), we have
![]() (2.22)
(2.22)
for sufficiently large k.
Duo to (2.21) and (2.22), we get
![]() (2.23)
(2.23)
which implies that![]() . Hence, there exists positive constant
. Hence, there exists positive constant ![]() such that
such that![]() , holds for all large k, which contradicts to (2.18).
, holds for all large k, which contradicts to (2.18).
Case (2): T is infinite. Then we have from (2.6) and (2.17) that
![]() (2.24)
(2.24)
which implies that
![]() (2.25)
(2.25)
The above equality together with the updating rule of (2.12) means
![]() (2.26)
(2.26)
Similar to (2.20), it follows from (2.25) and (2.26) that
![]()
for some positive constant![]() . Then we have
. Then we have
![]()
This equality together with (2.24) yields
![]()
which implies that
![]() (2.27)
(2.27)
It follows from (2.8), (2.27), (2.26) and (2.20) that
![]() (2.28)
(2.28)
Since ![]() from (2.8), we have from (2.13), (2.17) and (2.28) that
from (2.8), we have from (2.13), (2.17) and (2.28) that
![]()
which means
![]() (2.29)
(2.29)
By the same analysis as (2.23) we know that
![]() (2.30)
(2.30)
Hence, there exists a positive constant ![]() such that
such that ![]() holds for all sufficiently large k, which gives a contradiction to (2.29). The proof is completed. ♢
holds for all sufficiently large k, which gives a contradiction to (2.29). The proof is completed. ♢
3. Numerical Experiments
In this section, we test the performance of Algorithm 2.1 on the unconstrained nonlinear optimization problem, and compared it with a regularized Newton method without correction. The function to be minimized is
![]() (3.1)
(3.1)
where ![]()
![]() are constants. It is clear that function
are constants. It is clear that function ![]() is convex and the minimizer set of
is convex and the minimizer set of ![]() is
is
![]()
The Hessian ![]() is given by
is given by
![]()
where![]() ,
,![]() . Matrix
. Matrix ![]() is positive semidefinite for all x, but
is positive semidefinite for all x, but
singular as the sum of every column is zero. Since the Hessian ![]() is always singular, the Newton method cannot be used to solve nonlinear Equations (1.2). But by using the regularization technique, both regularized Newton method and Algorithm 2.1 work quite well.
is always singular, the Newton method cannot be used to solve nonlinear Equations (1.2). But by using the regularization technique, both regularized Newton method and Algorithm 2.1 work quite well.
The aims of the experiments are as follows: to check whether Algorithm 2.1 converges quadratically as stated in Section 3 and also to see how well the technique of correction works. We set![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() for Algorithm 2.1.
for Algorithm 2.1.
Table 1 reports the norms of ![]() at every iteration when
at every iteration when![]() ,
, ![]() ,
,
![]() and
and![]() . Algorithm 2.1 only take four iterations to obtain the minimizer of
. Algorithm 2.1 only take four iterations to obtain the minimizer of![]() ;
; ![]() decreases very quickly. The results show the sequence
decreases very quickly. The results show the sequence ![]() quadratic convergence. The iteration is as follows
quadratic convergence. The iteration is as follows
![]()
![]()
![]()
![]()
![]()
We may observe that the whole sequence ![]() converges to
converges to![]() .
.
We also ran the regularized Newton algorithm (RNA) without correction, that is, we do not solve the linear equations (2.9)-(2.10) and just set the solution of (2.8) to be the trial step. Then, we tested the regularized Newton algorithm without correction and Algorithm 2.1 for various of n, ![]() and different choices of the starting point. The results are listed in Table 2.
and different choices of the starting point. The results are listed in Table 2.![]() : the selected value of
: the selected value of![]() ; Dim: the dimension n of the problem;
; Dim: the dimension n of the problem;![]() : the ith element
: the ith element![]() ; niter: the number of iterations required;
; niter: the number of iterations required;![]() : the final value of
: the final value of![]() ;
;![]() : the final value of
: the final value of![]() . We use
. We use ![]() as the stopping criterion.
as the stopping criterion.
![]()
Table 1. Results of Algorithm 2.1 to test quadratic convergence.
![]()
Table 2. Results of RNA and Algorithm 2.1.
Moreover, we can see for the same![]() , n and
, n and![]() , the number of iterations of Algorithm 2.1 is always less than that of RNA. And the correction term does help to improve RNA when the initial point is far away from the minimizer. These facts indicate that the introduction of correction is really useful and could accelerate the convergence of the regularized Newton method.
, the number of iterations of Algorithm 2.1 is always less than that of RNA. And the correction term does help to improve RNA when the initial point is far away from the minimizer. These facts indicate that the introduction of correction is really useful and could accelerate the convergence of the regularized Newton method.
4. Concluding Remarks
In this paper, we propose a regularized Newton method with correction for unconstrained convex optimization. At every iteration, not only a RNM step is computed but also two correction steps are computed which make use of the previous available Jacobian instead of computing the new Jacobian. Numerical experiments suggest that the introduction of correction is really useful.
Acknowledgements
This research is supported by the National Natural Science Foundation of China (11426155) and the Hujiang Foundation of China (B14005).
NOTES
![]()
*Corresponding author.