Optimal Solution of Multi-Choice Mathematical Programming Problem Using a New Technique ()
Received 28 January 2016; accepted 7 March 2016; published 10 March 2016

1. Introduction
Most of real life and industrial problems involve a process called optimization, which means finding the maximum or minimum value of some quantity called objective function, subject to a system of linear inequa- lities or equalities called constraints. The graph of the system of constraints is called the feasible region and the optimal values of the objective function occur at vertices of the feasible region. Many research papers handle this problem from more than one point of view and gave very helpful and considerable results.
Linear programming is frequently applied in real-life problems and therefore it is very important to introduce new tools in the approach that allow the model to fit into the real-life problems. Linear programming was developed by Dantzig [5] . Linear programming has been applied to various decision making problems. Most extensively it is used in business and some industrial engineering problems. Some industries that use linear programming models include transportation, production planning and scheduling, energy, telecommunications, and manufacturing. It has been proved useful in modeling diverse types of problems in planning, routing, scheduling, assignment, and design. Any linear programming model representing real-world situations involves a lot of parameters whose values are assigned by the experts, and in the conventional approach, they are required to fix an exact value to the aforementioned parameters. However, both experts and the decision-maker fre- quently do not precisely know the value of those parameters, in most cases they depend only on statistical inference from past data and their stability is doubtful, so the parameters of the problem are usually defined by the decision maker in a uncertain way or by means of language statement parameters. Approaches to decision making under uncertainty have followed a variety of modeling philosophies, including minimization of expected value of loss, minimization of deviations from goals, minimization of costs and maximization of profits. The main approaches to decision making under uncertainty include stochastic and fuzzy programming. However, in some cases it is believed that the parameters or coefficients in the decision making problems are multi-choice in nature.
Chang [2] has recently proposed a new technique for modeling the multi-choice goal programming. In other paper [3] , he replaces multiplicative terms of binary variable by a continuous variable. An alternative approach for solving such kind of problem is chance constrained programming by Birge and Louveaux [6] and Sahoo & Biswal [10] . Many of the developments in the area of fuzzy mathematical programming are based on the paper written by Bellman and Zadeh [11] .
2. Mathematical Model
The mathematical model of a multi-choice linear programming problem is presented as:
Find 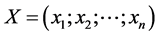 so as to:
so as to:
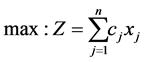 (1)
(1)
subject to:
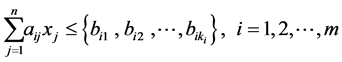 (2)
(2)
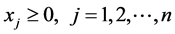 (3)
(3)
The right hand side of each constraint (2) has a set of 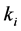 number of goals where only one goal is to be selected. To solve the multi-choice linear programming problem (1)-(3) it is necessary to transform the problem to a standard mathematical programming problem. In the coming section a general linear transformation is presented for all cases. our technique works not only for small values of
number of goals where only one goal is to be selected. To solve the multi-choice linear programming problem (1)-(3) it is necessary to transform the problem to a standard mathematical programming problem. In the coming section a general linear transformation is presented for all cases. our technique works not only for small values of  but also for the large values.
but also for the large values.
3. Linear Transformation
Let  denote the set of values (choices) in the right hand side of the
denote the set of values (choices) in the right hand side of the 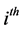 constrain with total number
constrain with total number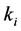 .
.
Setting:
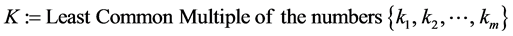 (4)
(4)
In order to achieve our main aim of selecting just one value among the 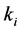 choices, our idea depend on
choices, our idea depend on
inserting a set of K binary variables, namely:  to construct a set of
to construct a set of 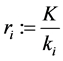 linear combinations in
linear combinations in
the following form:
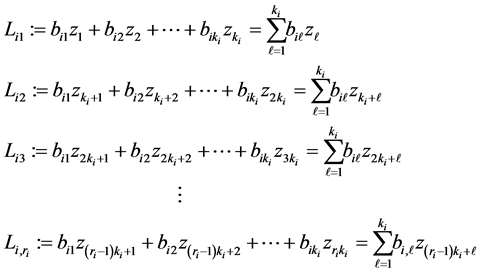 (5)
(5)
Finally, we replace the right hand side of the 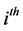 constrain by the expression:
constrain by the expression:
![]() (6)
(6)
Now, we can rewrite the mathematical model (1)-(3) in more convenient form as:
Find ![]() so as to:
so as to:
![]() (7)
(7)
subject to:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where ![]() given in (6). The restriction
given in (6). The restriction ![]() mentioned in (10) implies that one and only one of the
mentioned in (10) implies that one and only one of the
![]() binary variable will take the value one while the remaining
binary variable will take the value one while the remaining ![]() will take the value zero which ensures the achievement of our main aim of selecting a unique parameter value among the
will take the value zero which ensures the achievement of our main aim of selecting a unique parameter value among the ![]() values in the right hand side of each constrain.
values in the right hand side of each constrain.
4. Illustrative Numerical Example
A factory produce three different types of washing machines A, B, and C. Producing of one washing machine of type A requires 10 hours general labor, 5 technical hours, and 1 packing hour. While the washing machine of type B requires 4 hours general labor, 7 technical hours, and 2 packing hours. and the washing machine of type C requires 5 hours general labor, 2 technical hours, and 3 packing hours. The factory can afford up to 900 or 1000 or 1100 hours of general labor, up to 1000 or 1450 or 1600 or 2000 hours of technical labor, and up to 300 or 400 packing hours per week. A washing machine of type A, type B, and type C earns a profit of £130, £100, and £80 respectively. The factory decided to produce at least 20 washing machines of type C per week. How many washing machines per week should the factory produce from each type to maximize profit?
Let![]() ,
, ![]() , and
, and ![]() denote the number of produced washing machines of type A, B, and C per week respectively.
denote the number of produced washing machines of type A, B, and C per week respectively.
The following table summarize the information above:
Since the manufacturer wants to maximize the profit, so, we have the following mathematical multi-choice problem:
![]() (11)
(11)
subject to the constrains:
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Applying the above technique in (5) and (6), we can transform the given multi-choice programming problem to a mixed integer linear programming problem. Referring to the data above, we have![]() . So,
. So, ![]() which denotes the least common multiple of the integers (3,4,2). Therefore, we insert 12 binary variables in the right hand side of the three constraints and rewrite the problem in the the new form:
which denotes the least common multiple of the integers (3,4,2). Therefore, we insert 12 binary variables in the right hand side of the three constraints and rewrite the problem in the the new form:
![]() (16)
(16)
subject to:
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
The above mathematical model is treated by either LINGO or MATLAB software.
The corresponding Matlab code is:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The solution is obtained as: ![]() where the maximum profit is £21,800. The all binary variables are zeros except
where the maximum profit is £21,800. The all binary variables are zeros except ![]() take the value one which means that the choice of the goals of first, second and third constraints are 1100 gal, 1450 gal and 400 hours respectively. One can follow the techniques in [8] [9] to obtain the same solution.
take the value one which means that the choice of the goals of first, second and third constraints are 1100 gal, 1450 gal and 400 hours respectively. One can follow the techniques in [8] [9] to obtain the same solution.
5. Discussion and Conclusions
Biswal and Acharya [8] treat the problem of multi-choice linear programming problem by replacing the right hand side of each constraint with a specific mathematical expressions involving the multi-choice values multi- plied by polynomials of binary variables, those expressions change from one constraint to another according to the number of multi-choice values in that constraint. Moreover, some restrictions are imposed on the binary variable to obtain just one value in the right hand side of each constraint. In their other paper [9] , they replaced the right hand side of each constraint with an interpolating polynomial more precisely, assuming that the ![]() constraint contains
constraint contains ![]() multi-choice values then the corresponding interpolating polynomial will be of degree
multi-choice values then the corresponding interpolating polynomial will be of degree ![]() which gives just one value among the
which gives just one value among the ![]() values corresponding to each value of the independent variable
values corresponding to each value of the independent variable![]() . The technique in this paper transforms the right hand side of each constraint to a linear combination with the same number of terms which enable us to treat the problem as a usual linear programming problem. Indeed, using different softwares we found that our technique gives the same results as [8] [9] .
. The technique in this paper transforms the right hand side of each constraint to a linear combination with the same number of terms which enable us to treat the problem as a usual linear programming problem. Indeed, using different softwares we found that our technique gives the same results as [8] [9] .
The aim of the article was to describe a new efficient technique for solving mathematical multi-choice problems the process depend on obtaining a number of linear mathematical expressions equal to the number of the multi-choice constrains and contain a specified number of binary variables. We tried to set the models as general as possible and that way make them applicable to any given mathematical multi-choice linear pro- gramming task. In practice it is possible to describe the majority of such problems. We can state that these models can serve as a simple and easy method for solving this type of mathematical problems using available softwares as Matlab and Lingo. Transforming the multi-choice problem to a linear problem is considered the main advantage of this method. The present method can be extended to a multi-objective multi-choice linear programming problem.
Acknowledgements
The authors are thankful to the editor in chief and the learned referees for their valuable suggestions regarding the improvement of this paper.
NOTES
![]()
*Corresponding author.