Behaviour of Earth Dam under Seismic Load Considering Nonlinearity of the Soil ()
Received 14 October 2015; accepted 5 March 2016; published 8 March 2016

1. Introduction
Earthen dams are very important structure and provide renewable energy and agriculture facility to the country. As the dams’ structure is very large and the dams store tremendous amount of water, with respect to environmental and economic considerations, their safe performance is very important. Stability and performance are always primary concerns for any structure such as the huge structure of dams and the failure of it which causes disaster and loss of human being and properties in results. Despite significant development in geotechnical engineering, earthquakes continue to cause failure of many dams and result in the destruction of life and the damage of properties, so the stability of earthen dams during earthquake is of primary concern.
Earthen dams are preferred over the concrete gravity dam due to simple construction and relative economical advantage. Locally available materials and less skills labor reduce the construction cost thus it is still widely used. Dams have made an important and significant contribution in development of human being and society. The benefits derived from dams are always considerable in the field of renewable energy and agriculture and very important to control floods.
Core dam is a type of earthen dam where a compacted central clay core is supported on the upstream and downstream sides by compacted shell materials. The core is separated from the compacted shells by a series of transition zones build of the well-graded material, however if well-graded materials such as sand are used in shells, there are no requirements of such zones. Materials used in the shells are generally medium to dense sand and due to pervious nature of sand it allows the seepage through it which is the point of concern. Laboratory and field test of these materials are easy as compared to rock-fill materials which are large and irregular in size.
Like most engineering structures, earth dams can fail due to faulty design, inadequate construction practices and poor maintenance, etc. Performance evaluation and the stability of earth dams during earthquakes require a dynamic response analysis to determine acceleration, dynamic stresses and deformations induced in the dam by the seismic forces. In current engineering practice, dynamic response of earth dams (located in valleys or narrow canyons) undergoing high-magnitude earthquakes is generally determined by independently calculating the dynamic response of the various sections of the dam performing a finite element analysis.
There are two important issues to be solved in the assessment of seismic behavior of earth dams under earthquakes:
1) Stability: Is dam stable during and after earthquake?
2) Deformation: How much deformation will occur in the dam?
The possible forms of failure of earth dams due to earthquakes have been recruited by Sherard. It was stated that: a) Disruption of dam caused by major fault movement at base; b) lack of slope ground movement; c) loss induced freeboard, due to the difference of the movements of tectonic ground; d) loss due to freeboard slope failure or soil compaction movements induced ground failure; e) piping through cracks due to earthworks; f) the overflow of dam due to slides or rock falls in the tank; g) slip of dams on weak foundation materials; and h) failure spillway or outlet works [1] .
Using a traditional approach, the stability of large earthen dam in static condition is studied with the limit equilibrium method [2] , while the dynamic response of such a structure is analyzed by a pseudo-static analysis, the displacement method derived from Newmark’s rigid block method [3] . Slopes become unsafe when shear stresses of potential surface are more than shearing resistance of the soil [4] . “Slides can occur in practically all possible manner, gradually or rapidly and by or short of several superficial hassle” [5] . IITK-GSDMA recommended an equivalent static method for the dynamic analysis using the seismic coefficient of earthquake [6] . Newmark presented the ideas of dynamic stability for dam in terms of deformation rather than the factor of safety. [3] engaged dynamic stress deformation finite element analysis to yield the time variable horizontal resulting force acting on failure surface [7] . Finite element method is a modern computer oriented approach to analysis for complex structure of arbitrary shapes [8] . There are two methods of the finite element analysis [9] [10] :
1) Flexibility or force method and
2) Stiffness or displacement method.
Finite element method is used to analyze a two-dimensional earthen dam section. To observe effects of nonlinearity of soil, linear and nonlinear soil models are used in the analysis using software GeoStudio (2012) [11] and results are obtained in terms of contour of stresses and displacements to observe the performance of the earthen dam in case of earthquake loads.
2. Problem Statement
A case study of Nara earth dam is taken which is a low dam of height 40 m. This dam is located on Kandi canal in Kandi area of district Hoshiarpur, Punjab. It is a medium size zoned dam near Barrian Wala village along Shivalik hill providing irrigation facilities and flood control. The Kandi canal area is situated 16 km from the Hoshiarpur. The dam lies in seismic zone IV as per seismic zoning map of India mention in I.S code for earthquake resistant design of structures [12] .
2.1. Cross Section of Dam and Material Properties
Nara dam is a zoned dam and divided in core and shell. The cross section of the dam is shown in Figure 1. The height and length of the dam are considered as 40 m and 270.5 m respectively. The crest length of the dam is 15 m. The water freeboard in upstream is about 4 m and in downstream side has a tail water of 4 m. The core started from 12 m below from the point where shell started and the height of the core is just 1 m short of the dam height and top crest of the core is about 10 m. The material properties of the shell and core are given in Table 2. For calculation of shear modulus, an average shear wave velocity of 235 m/s is taken for both materials.
2.2. Modelling of the Dam
The 2D finite element model of Nara dam with all boundary conditions is shown in Figure 2. The meshing is done using quadrilateral and triangular elements of 5 m element size with secondary nodes of element size of 1 m for core and shell regions. A total number of 814 nodes and 243 elements have been used for the modeling of the dam. The bottom of the dam is modeled fix in both x and y directions. The model is analyzed for full reservoir conditions with upstream water level at 36 m and having 4 m tail water. To compute stresses correctly, it is necessary to apply the weight of the reservoir as boundary condition. The soil in the core and shell region is assigned by the linear and elastic plastic soil model to observe effect of nonlinearity.
2.3. Formulation
In finite element analysis of dam, the problem is treated as two dimensional and the dam cross-section is represented an assemblage of constant strain triangular and quadrilateral elements. The element used in the present investigation is a plain strain quadrilateral element composed of two four nodal point triangles.
The element stiffness matrix is a function of the matrix is a function of the geometric and constitutive properties of element. The stiffness [K] of the complete structural assemblage may be obtained from the individual from the individual element stiffness matrices by direct stiffness assembly procedures.
The equation of motion for two-dimensional structure, idealized as a plane strain finite element system, subjected to dynamic loads, may be expressed in matrix form as
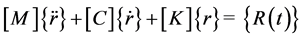 (1)
(1)
In Equation (1), [M] and [K] are the mass and stiffness matrices and [C] is a viscous damping matrix for the finite element system. {r} is the vector of 2N nodal points in the finite element idealization: 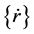 and
and 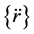 are respectively the nodal point velocity and acceleration vectors. In the case of earthquake excitation, the load vector
are respectively the nodal point velocity and acceleration vectors. In the case of earthquake excitation, the load vector 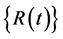 is a function of the nodal point masses and accelerations.
is a function of the nodal point masses and accelerations.
3. Results and Discussion
3.1. Static Analysis
The first step is to establish the in situ stress state conditions using SIGMA/W that exist before the earthquake occurs, using linear elastic model and nonlinear (elastic-plastic) model respectively. The most important soil properties required for linear elastic model are unit weights and Poisson’s ratios while for elastic-plastic model, the material properties required for this model are unit weights, Poisson’s ratios, young’s modulus and c-φ of the soil are listed in Table 1. The contours of vertical and horizontal stresses are shown in Figure 3 for elastic plas-
![]()
Table 1. Material properties of different sections of the dam [13] .
![]() (a)
(a)![]() (b)
(b)
Figure 3. Contours of (a) vertical stress and (b) horizontal stress for elastic plastic model using SIGMA/W.
tic model as contours of horizontal as well as vertical stresses for linear elastic and elastic plastic model found to be same. In both case, contours of horizontal as well as vertical stresses, it is observed that the stress increases from top to bottom of the dam, which is as expected. Also stresses decreases towards the edges of the dams. The maximum horizontal stress and maximum vertical stress found to be 720.25 kPa and 884.50 kPa respectively.
3.2. Seismic Analysis
The seismic analysis is carried out for linear elastic and nonlinear(elastic-plastic) model soil models. The results of static analysis are used as initial conditions for seismic analysis using QUAKE/W. The material properties of soil required for dynamic analysis are total unit weight, Poisson’s ratio, elastic modulus, c-phi and damping ratio. For the seismic analysis, damping ratio value is considered as 0.1 (10%). The time history of Kashmir earthquake (2005) of magnitude 7.6 is used as the horizontal ground motion whose initial peak is 0.12 g and modified to 0.24g as the site is located in seismic zone IV. The actual and modified time history is shown in Figure 4(a) and Figure 4(b). The results of seismic analysis for each soil model are presented in the form of contours of vertical stresses, horizontal stresses, vertical displacement and horizontal displacement.
3.3. Effects of Nonlinearity
The contours of vertical stresses of linear, and nonlinear soil model are shown in Figure 5(a) and Figure 5(b) respectively. It is observed that in both cases the vertical stresses are increases from top to bottom of the dam which is expected. The maximum vertical stresses for linear soil model is 958.2 kPa and for nonlinear (elastic- plastic) soil model it is 1031.5 kPa which shows, as the nonlinearity increases stresses increases while minimum vertical stresses for these cases are found to be in the toe of dam which are −25.741 kPa and −23.701 kPa respectively shows that effect of tensioning decreases with nonlinearity of the soil.
The contours horizontal stresses of linear and nonlinear soil models are shown in Figure 6(a) and Figure 6(b) respectively.
It is observed that in all three cases the horizontal stresses are increases from top to bottom of the dam which is expected. The maximum horizontal stresses for linear soil model is 753.69 kPa and for nonlinear soil model it is 808.94 kPa which shows, as the nonlinearity increases stresses increases while minimum vertical stresses for these cases are found to be in the toe of dam which are −14.355 kPa and −8.3208 kPa respectively shows that effect of tensioning decreases with nonlinearity of the soil.
![]()
![]() (a) (b)
(a) (b)
Figure 4. (a) Actual time history of Kashmir earthquake (2005) with peak value of 0.12 g, (b) modified time history of Kashmir earthquake (2005) with peak value of 0.24 g.
![]() (a)
(a)![]() (b)
(b)
Figure 5. The contours of vertical stresses of (a) linear and (b) nonlinear soil model.
![]() (a)
(a)![]() (b)
(b)
Figure 6. The contours of horizontal stresses of (a) linear and (b) nonlinear soil model.
The contours vertical displacements of linear and nonlinear soil model are shown in Figure 7(a) and Figure 7(b).
![]() (a)
(a)![]() (b)
(b)
Figure 7. The contours of vertical displacements of (a) linear and (b) nonlinear soil model.
The maximum vertical displacement of linear and nonlinear soil models are decreasing from top to bottom and found to be 28.751 cm and 30.526 cm respectively. The increasing trend of vertical displacement from linear to nonlinear soil models show that the effect of nonlinearity of the soil started, which is expected.
The contours horizontal displacements of linear and nonlinear soil model are shown in Figure 8(a) and Figure 8(b) respectively.
The maximum horizontal displacement of linear, equivalent linear and nonlinear soil models is found to be 5.608 mm and 11.470 mm respectively. The increasing trend of horizontal displacement shows the effect of nonlinearity of the soil which is expected.
The results of the seismic analysis of Nara dam are summarized in Table 2.
From the results reported in above table it observed that the value of stresses and displacement increase from linear to nonlinear soil model which shows the effect of nonlinearity of the soil.
4. Conclusion
After the static and dynamic analysis of the Nara dam, it is found that the contours of horizontal and vertical stresses increase from top to bottom of the dam which is expected. It is observed that the soil behaves linearly during the static analysis. But after the seismic analysis due to effect of nonlinearity of the soil stresses and displacements, it increases from linear elastic to nonlinear (elastic plastic) soil model. The contours of horizontal and vertical displacements decrease from top to bottom of the dam. The value of maximum horizontal as well as vertical settlements is within permissible limit as per I.S codeis 1% - 2% of the earthen dam height [14] . In case of horizontal displacement, effect of nonlinearity is very high almost double of the linear soil model.
![]() (a)
(a)![]() (b)
(b)
Figure 8. The contours of horizontal displacements of (a) linear and (b) nonlinear soil model.
![]()
Table 2. Results of the nara dam for seismic analysis.
Acknowledgements
I am very thankful to my M.TECH supervisor, Prof. B. K. Maheshwari for his sincere support and guidance. I am also thankful to Prof. M. L. Sharma, head of the department, other teachers and technical staffs for their continuous support and help.