New Generalized (G'/G)-Expansion Method Applications to Coupled Konno-Oono Equation

Md. Nur Alam^1*, Fethi Bin Muhammad Belgacem²

¹Department of Mathematics, Pabna University of Science & Technology, Pabna, Bangladesh.
²Department of Mathematics, Faculty of Basic Education, PAAET, Al-Ardhiya, Kuwait.

DOI: 10.4236/apm.2016.63014                

Abstract

The new generalized (G'/G)-expansion method is one of the powerful and competent methods that appear in recent time for establishing exact solutions to nonlinear evolution equations (NLEEs). We apply the new generalized (G'/G)-expansion method to solve exact solutions of the new coupled Konno-Oono equation and construct exact solutions expressed in terms of hyperbolic functions, trigonometric functions, and rational functions with arbitrary parameters. The significance of obtained solutions gives credence to the explanation and understanding of related physical phenomena. As a newly developed mathematical tool, this method efficiency for finding exact solutions has been demonstrated through showing its straightforward nature and establishing its ability to handle nonlinearities prototyped by the NLEEs whether in applied mathematics, physics, or engineering contexts.

Keywords

New Generalized (G'/G)-Expansion Method, Coupled Konno-Oono Equations, Nonlinear Partial Differential Equation

Received 10 November 2015; accepted 24 February 2016; published 29 February 2016

1. Introduction

Various physical, mechanical, chemical, biological, engineering and some economic laws and relations appear mathematically in the form of differential equations which are linear or nonlinear, homogeneous or inhomogeneous. Almost all differential equations relating physical phenomena are nonlinear. Methods of solutions of linear differential equations are reasonably easy and well avowed. In contrast, the techniques of solutions of nonlinear differential equations are less obtainable and in general, approximations are generally used. Nonlinearity is a fascinating element of nature, today; many scientists observe nonlinear science as the most important frontier for the fundamental understanding of nature. The analytical solutions of such equations are of fundamental importance to reveal the inner structure of the phenomena. The world around us is inherently nonlinear. For instance, nonlinear evolution equations (NEEs) are widely used as models to describe complex physical phenomena in various fields of sciences, especially in fluid mechanics, solid-state physics, plasma physics, plasma waves and biology, etc. One of the basic physical problems for those models is to obtain their travelling wave solutions. In particular, various methods have been utilized to explore different kinds of solutions of physical models described by nonlinear partial differential equations (NPDEs). In the numerical methods, stability and convergence should be considered so as to avoid divergent or inappropriate results. However, in recent years, a variety of effective analytical and semi-analytical methods have been developed to be used for solving NLEEs, such as the inverse scattering transform method [1] , the 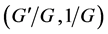-expansion method [2] [3] , the modified simple equation method [4] [5] , the Sumudu transform method [6] -[8] , the homogeneous balance method [9] [10] , the Darboux transformation method [11] , the Backlund transformation method [12] , the complex hyperbolic function method [13] [14] , the 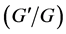-expansion method [15] -[25] , the improved -expansion method [26] , the collocation method [27] [28] , the similarity reductions method [29] [30] , the homotopy analysis method [31] [32] , the spectral-homotopy analysis method [33] -[35] , the Hermite-Pade approximation method [36] and so on.

Naher and Abdullah [37] introduced a new approach of 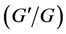-expansion method and a new approach of generalized 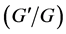-expansion method for a reliable treatment of the nonlinear evolution equations. Afterwards, many researchers investigated many nonlinear PDEs to construct traveling wave solutions via this powerful -expansion method. For example, Alam and Akbar [38] [39] applied this method for finding traveling wave solutions of the KP-BBM equation, the (3 + 1)-dimensional potential-YTSF equation, the (2 + 1)-dimen- sional Zakharov-Kuznetsov equation. Alam et al. [40] [41] concerned about this method to construct traveling wave solutions of the strain wave equation in microstructured solids, the (3 + 1)-dimensional mKdV-ZK equation and the (1 + 1)-dimensional compound KdVB equations. The objective of this article is to look for new study relating to the new generalized expansion method for solving the new coupled Konno-Oono equation to make the goodwill and helpfulness of the method obvious.

Our aim in this paper is to present an application of the new generalized 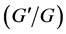-expansion method to the new coupled Konno-Oono equation to be solved by this method for the first time.

The rest of the paper is organized as follows: In Section 2, we give the description of the new generalized 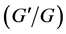-expansion method. In Section 3, we apply this method to the new coupled Konno-Oono equation with discussion and Graphical representations of the solutions. Conclusions are given at last.

2. Description of the Method

Let us consider a general nonlinear PDE in the form

, (1)

where 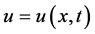is an unknown function, P is a polynomial in and its derivatives in which highest order derivatives and nonlinear terms are involved and the subscripts stand for the partial derivatives.

Step 1: We combine the real variables x and t by a complex variable

, , (2)

where V is the speed of the traveling wave. The traveling wave transformation (2) converts Equation (1) into an ordinary differential equation (ODE) for:

, (3)

where Q is a polynomial of u and its derivatives and the superscripts indicate the ordinary derivatives with respect to.

Step 2: According to possibility Equation (3) can be integrated term by term one or more times, yields constant(s) of integration. The integral constant may be zero, for simplicity.

Step 3: Suppose the traveling wave solution of Equation (3) can be expressed as follows:

, (4)

where either or may be zero, but both or could be zero at a time, and and d are arbitrary constants to be determined later and is

(5)

where satisfies the following auxiliary ordinary differential equation:

(6)

where the prime stands for derivative with respect to; A, B, C and E are real parameters.

Step 4: To determine the positive integer N, taking the homogeneous balance between the highest order nonlinear terms and the derivatives of the highest order appearing in Equation (3).

Step 5: Substitute Equation (4) and Equation (6) including Equation (5) into Equation (3) with the value of N obtained in Step 4, we obtain polynomials in and . Then, we collect each coefficient of the resulted polynomials to zero, yields a set of algebraic equations for and , d and V.

Step 6: Suppose that the value of the constants , , d and V can be found by solving the algebraic equations obtained in Step 5. Since the general solution of Equation (6) is well known to us, inserting the values of , , d and V into Equation (4), we obtain more general type and new exact traveling wave solutions of the nonlinear partial differential Equation (1).

Using the general solution of Equation (6), we have the following solutions of Equation (5):

Family 1: When and

(7)

Family 2: When and

(8)

Family 3: When and

(9)

Family 4: When and

(10)

Family 5: When and

(11)

3. The New Coupled Konno-Oono Equation

The new coupled Konno-Oono equation: In this section, we will put forth the new generalized expansion method to construct many new and more general traveling wave solutions of the new coupled Konno-Oono equation. Let us consider the new coupled Konno-Oono equation [42] [43] ,

(12)

Now let us suppose that the traveling wave transformation equation be

(13)

The Equation (13) reduces Equation (12) into the following ODEs

(14)

(15)

By integrating (15) with respect to, we obtain

(16)

where P is a constant of integration.

Substituting Equation (16) into Equation (14), we get

(17)

Taking the homogeneous balance between highest order nonlinear term and linear term of the highest order in Equation (17), we obtain. Therefore, the solution of Equation (17) is of the form:

(18)

where and d are constants to be determined.

Substituting Equation (18) together with Equations (5) and (6) into Equation (17), the left-hand side is converted into polynomials in and . We collect each coefficient of these resulted polynomials to zero yields a set of simultaneous algebraic equations (for simplicity, the equations are not presented) for, , , d, P and V. Solving these algebraic equations with the help of computer algebra, we obtain following:

, , (19)

where d, A, B, C, E are free parameters.

Substituting Equation (19) into Equation (18), along with Equation (7) and simplifying, our traveling wave solutions become, if but but respectively:

and

and

Substituting Equation (19) into Equation (18), along with Equation (8) and simplifying yields exact solutions, if but but respectively:

and

and

Substituting Equation (19) into Equation (18), along with Equation (9) and simplifying, our obtained solution becomes:

and

Substituting Equation (19) into Equation (18), together with Equation (10) and simplifying, yields following traveling wave solutions, if but but respectively:

.

and

.

and

Substituting Equation (19) into Equation (18), along with Equation (11) and simplifying, our exact solutions become, if but but respectively:

and

,

and

.

where

Khan and Akbar [43] investigated solutions of the the new coupled Konno-Oono equation by the modified simple equation method and obtained only eight solutions (A1)-(A8) (see appendix). Moreover, in this article eighteen solutions of the new coupled Konno-Oono equation are constructed by applying the new approach of generalized -expansion method. But by means of the new approach of generalized -expansion method we obtained solutions are different to Khan and Akbar [43] solutions. Furthermore, we obtain solutions,. These solutions are new and were not obtained by Khan and Akbar [43] . On the other hand, the auxiliary equation used in this paper is different, so obtained solutions is also different.

4. Graphical Representations of the Solutions

The graphical illustrations of the solutions are depicted in the Figures 1-6 with the aid of commercial software Maple.

Figure 1. Single soliton of when A = 4, B = 1, C = 1, E = 1, d = 1, and.

Figure 2. Multiple soliton of when , , and.

Figure 3. Compacton of when , , and.

Figure 4. Singular soliton of when , , and.

Figure 5. Singular periodic solution of when and.

Figure 6. Periodic solutions of when and.

5. Conclusion

The new generalized -expansion method presented in this paper has been successfully implemented to construct many new and more general exact solutions of the new coupled Konno-Oono equation. The method offers solutions with free parameters that might be important to explain some complex physical phenomena. Comparing the currently proposed method with other methods, such as -expansion method, the Exp- function method and the modified simple equation method, we might conclude that the exact solutions to Equation (12) can be investigated using these methods with the help of the symbolic computation software such as Matlab, Mathematica and Maple to facilitate the complicated algebraic computations. This study shows that the new generalized -expansion method is quite efficient and practically well suited to be used in finding exact solutions of NLEEs. Also, we observe that the new generalized -expansion method is straightforward and can be applied to many other nonlinear evolution equations.

Acknowledgements

F.B.M. Belgacem is pleased to acknowledge the continued support of the Public Authority Applied Education and Training Research Department (PAAET RD).

Appendix: Khan and Akbar’s Solutions [43]

We bring to the reader’s attention that Equation (16) regarding v(x,t) above is the same as Equation (10) in Khan and Akbar [43] , where the authors manged established exact solutions of the new coupled Konno-Oono equation by using the modified simple equation method which are as follows (see Equation (23) for u(x,t), in [43] ):

(A.0)

We can freely choose the constants A and B. Therefore, setting, Equation (A.0) reduces to

(A.1)

(A.2)

Again, Setting, Equation (A.0) reduces to

(A.3)

(A.4)

If, using hyperbolic function identities, from (A.0), we get the following periodic traveling wave solutions:

(A.5)

(A.6)

(A.7)

(A.8)

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Ablowitz, M.J. and Clarkson, P.A. (1991) Soliton, Nonlinear Evolution Equations and Inverse Scattering Method. Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9780511623998
[2]	Yang, Y.J. (2013) New Application of the (G’/G,1/G)-Expansion Method to KP Equation. Applied Mathematical Sciences, 7, 959-967.
[3]	Li, L.X., Li, E.Q. and Wang, M.L. (2010) The (G’/G,1/G)-Expansion Method and Its Application to Traveling Wave Solutions of the Zakharov Equations. Applied Mathematics, 25, 454-462. http://dx.doi.org/10.1007/s11766-010-2128-x
[4]	Jawad, A.J.M., Petkovic, M.D. and Biswas, A. (2010) Modified Simple Equation Method for Nonlinear Evolution Equations. Applied Mathematics and Computation, 217, 869-877. http://dx.doi.org/10.1016/j.amc.2010.06.030
[5]	Khan, K., Akbar, M.A. and Alam, M.N. (2013) Traveling Wave Solutions of the Nonlinear Drinfel’d-Sokolov-Wilson Equation and Modified Benjamin-Bona-Mahony Equations. Journal of the Egyptian Mathematical Society, 21, 233-240. http://dx.doi.org/10.1016/j.joems.2013.04.010
[6]	Belgacem, F.B.M., Karaballi, A.A. and Kalla, S.L. (2003) Analytical Investigations of the Sumudu Transform and Applications to Integral Production Equations. Mathematical Problems in Engineering, 2003, 103-118.
[7]	Belgacem, F.B.M. (2006) Introducing and Analyzing Deeper Sumudu Properties. Nonlinear Studies, 13, 23-41.
[8]	Belgacem, F.B.M. and Karaballi, A.A. (2006) Sumudu Transform Fundamental Properties Investigations and Applications. Journal of Applied Mathematics and Stochastic Analysis, 2006, Article ID: 91083.
[9]	Zayed, E.M.E., Zedan, H.A. and Gepreel, K.A. (2004) On the Solitary Wave Solutions for Nonlinear Hirota-Sasuma Coupled KDV Equations. Chaos, Solitons and Fractals, 22, 285-303. http://dx.doi.org/10.1016/j.chaos.2003.12.045
[10]	Wang, M.L. (1996) Exact Solutions for a Compound KdV-Burgers Equation. Physics Letters A, 213, 279-287. http://dx.doi.org/10.1016/0375-9601(96)00103-X
[11]	Matveev, V.B. and Salle, M.A. (1991) Darboux Transformation and Solitons. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-00922-2
[12]	Miura, M.R. (1978) Backlund Transformation. Springer, Berlin.
[13]	Zayed, E.M.E., Abourabia, A.M., Gepreel, K.A. and Horbaty, M.M. (2006) On the Rational Solitary Wave Solutions for the Nonlinear HirotaCSatsuma Coupled KdV System. Journal of Applied Analysis, 85, 751-768. http://dx.doi.org/10.1080/00036810600604789
[14]	Chow, K.W. (1995) A Class of Exact Periodic Solutions of Nonlinear Envelope Equation. Journal of Mathematical Physics, 36, 4125-4137. http://dx.doi.org/10.1063/1.530951
[15]	Wang, M., Li, X. and Zhang, J. (2008) The (G’/G)-Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423. http://dx.doi.org/10.1016/j.physleta.2007.07.051
[16]	Alam, M.N. and Akbar M.A. (2015) A Novel (G’/G)-Expansion Method for Solving the (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation in Mathematical Physics. International Journal of Computing Science and Mathematics, 6, 404-415. http://dx.doi.org/10.1504/IJCSM.2015.071812
[17]	Feng, J., Li, W. and Wan, Q. (2011) Using (G’/G)-Expansion Method to Seek the Traveling Wave Solution of Kolmogorov-Petrovskii-Piskunov Equation. Applied Mathematics and Computation, 217, 5860-5865. http://dx.doi.org/10.1016/j.amc.2010.12.071
[18]	Alam, M.N. (2015) Exact Solutions to the Foam Drainage Equation by Using the New Generalized -Expansion Method. Results in Physics, 5, 168-177. http://dx.doi.org/10.1016/j.rinp.2015.07.001
[19]	Guo, S. and Zhou, Y. (2010) The Extended (G’/G)-Expansion Method and Its Applications to the Whitham-Broer-Like Equations and Coupled Hirota-Satsuma KdV Equations. Applied Mathematics and Computation, 215, 3214-3221. http://dx.doi.org/10.1016/j.amc.2009.10.008
[20]	Zhu, S.D. (2008) The Generalizing Riccati Equation Mapping Method in Nonlinear Evolution Equation: Application to (2+1)-Dimensional Boiti-Leon-Pempinelle Equation. Chaos, Solitons & Fractals, 37, 1335-1342. http://dx.doi.org/10.1016/j.chaos.2006.10.015
[21]	Alam, M.N., Akbar, M.A. and Mohyud-Din, S.T. (2014) A Novel (G’/G)-Expansion Method and Its Application to the Boussinesq Equation. Chinese Physics B, 23, Article ID: 020203. http://dx.doi.org/10.1088/1674-1056/23/2/020203
[22]	Shakeel, M., Ul-Hassan, Q.M. and Ahmad, J. (2014) Applications of the Novel (G’/G)-Expansion Method for a Time Fractional Simplified Modified MCH Equation. Abstract and Applied Analysis, 2014, Article ID: 601961.
[23]	Hafez, M.G., Alam, M.N. and Akbar, M.A. (2014) Exact Traveling Wave Solutions to the Klein-Gordon Equation Using the Novel (G’/G)-Expansion Method. Results in Physics, 4, 177-184. http://dx.doi.org/10.1016/j.rinp.2014.09.001
[24]	Alam, M.N. and Akbar, M.A. (2014) A New (G’/G)-Expansion Method and Its Application to the Burgers Equation. Walailak Journal of Science and Technology, 11, 643-658.
[25]	Zayed, E.M.E. (2009) New Traveling Wave Solutions for Higher Dimensional Nonlinear Evolution Equations Using a Generalized (G’/G)-Expansion Method. Journal of Physics A: Mathematical and Theoretical, 42, Article ID: 195202. http://dx.doi.org/10.1088/1751-8113/42/19/195202
[26]	Zhang, J., Jiang, F. and Zhao, X. (2010) An Improved (G’/G)-Expansion Method for Solving Nonlinear Evolution Equations. International Journal of Mathematics, 87, 1716-1725. http://dx.doi.org/10.1080/00207160802450166
[27]	Saliman, A.A. (2004) Collocation Solution of the Kortewegde Vries Equation Using Septic Splines. International Journal of Computer Mathematics, 81, 325-331. http://dx.doi.org/10.1080/00207160410001660817
[28]	Soliman, A.A. and Hussein, M.H. (2005) Collocation Solution for RLW Equation with Septic Spline. Applied Mathematics and Computation, 161, 623-636. http://dx.doi.org/10.1016/j.amc.2003.12.053
[29]	Bluman, G.W. and Kumei, S. (1989) Symmetries and Differential Equations. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4757-4307-4
[30]	Olver, P.J. (1986) Applications of Lie Groups to Differential Equations. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4684-0274-2
[31]	Domairry, G., Mohsenzadeh, A. and Famouri, M. (2009) The Application of Homotopy Analysis Method to Solve Nonlinear Differential Equation Governing Jeffery-Hamel Flow. Communications in Nonlinear Science and Numerical Simulation, 14, 85-95. http://dx.doi.org/10.1016/j.cnsns.2007.07.009
[32]	Joneidi, A.A., Domairry, G. and Babaelahi, M. (2010) Three Analytical Methods Applied to Jeffery-Hamel Flow. Communications in Nonlinear Science and Numerical Simulation, 15, 3423-3434. http://dx.doi.org/10.1016/j.cnsns.2009.12.023
[33]	Motsa, S.S., Sibanda, P., Awad, F.G. and Shateyi, S. (2010) A New Spectral-Homotopy Analysis Method for the MHD Jeffery-Hamel Problem. Computers & Fluids, 39, 1219-1225. http://dx.doi.org/10.1016/j.compfluid.2010.03.004
[34]	Makukula, Z.G., Sibanda, P. and Motsa, S.S. (2010) A Note on the Solution of the von Kármán Equations Using Series and Chebyshev Spectral Methods. Boundary Value Problems, 2010, Article ID: 471793.
[35]	Sibanda, P., Makukula, Z.G. and Motsa, S.S. (2010) A Novel Numerical Technique for Two-Dimensional Laminar Flow between Two Moving Porous Walls. Mathematical Problems in Engineering, 2010, Article ID: 528956.
[36]	Makinde, O.D. and Mhone, P.Y. (2006) Hermite-Padé Approximation Approach to MHD Jeffery-Hamel Flows. Applied Mathematics and Computation, 181, 966-972. http://dx.doi.org/10.1016/j.amc.2006.02.018
[37]	Naher, H. and Abdullah, F.A. (2013) New Approach of (G’/G)-Expansion Method and New Approach of Generalized (G’/G)-Expansion Method for Nonlinear Evolution Equation. AIP Advances, 3, Article ID: 032116. http://dx.doi.org/10.1063/1.4794947
[38]	Alam, M.N. and Akbar, M.A. (2014) The New Approach of Generalized (G’/G)-Expansion Method for Nonlinear Evolution Equations. Ain Shams Engineering Journal, 5, 595-603. http://dx.doi.org/10.1016/j.asej.2013.12.008
[39]	Alam, M.N. and Akbar, M.A. (2013) Exact Traveling Wave Solutions of the KP-BBM Equation by Using the New Approach of Generalized (G’/G)-Expansion Method. Springer Plus, 2, 617. http://dx.doi.org/10.1186/2193-1801-2-617
[40]	Alam, M.N., Akbar, M.A. and Mohyud-Din, S.T. (2014) General Traveling Wave Solutions of the Strain Wave Equation in Microstructured Solids via the New Approach of Generalized (G’/G)-Expansion Method. Alexandria Engineering Journal, 53, 233-241. http://dx.doi.org/10.1016/j.aej.2014.01.002
[41]	Alam, M.N., Akbar, M.A. and Hoque, M.F. (2014) Exact Traveling Wave Solutions of the (3+1)-Dimensional mKdV-ZK Equation and the (1+1)-Dimensional Compound KdVB Equation Using New Approach of the Generalized (G’/G)-Expansion Method. Pramana—Journal of Physics, 83, 317-329. http://dx.doi.org/10.1007/s12043-014-0776-8
[42]	Konno, K. and Oono, H. (1994) New Coupled Integrable Dispersion-Less Equations. Journal of the Phusical Society of Japan, 63, 377-378. http://dx.doi.org/10.1143/JPSJ.63.377
[43]	Khan, K. and Akbar, M.A. (2013) Traveling Wave Solutions of Some Coupled Nonlinear Evolution Equations. Mathematical Physics, 2013, Article ID: 685736.