Received 29 December 2015; accepted 22 February 2016; accepted 25 February 2016

1. Introduction
Most planetary bodies have been assumed to be spherical and consequently, many treatments of motion involving these bodies have been taken into consideration the spherical approximation of the bodies [1] - [3] . However, despite the spherical assumption of planetary bodies, studies have shown that the oblate spheroid is a more approximate description of these bodies [4] - [7] , thus the need for a description of the planetary bodies in terms of the oblate spheroidal coordinate system.
It is worth noting that the description of the planetary bodies mentioned so far have been based on the theory of orthogonal curvilinear coordinates [8] and with foundations on the Euclidean Geometry. However, following the presentation of the work of Riemann in 1854 which laid the foundations for the Riemannian Geometry, there had been considerable interest in the Riemannian Geometry. Consequently, in this paper, we employ the Metric Tensors in oblate spheroidal coordinate system [9] to derive the Riemannian acceleration for the oblate spheroidal coordinate system.
2. Mathematical Formulation
2.1. Oblate Spheroidal Coordinate
In this formulation we have chosen the spheroidal coordinate system based on the approximate representation of the planetary bodies as oblate spheroids. The surface generated by the rotation of an ellipse about its minor axis
is an oblate spheroid. The oblate spheroidal coordinate system 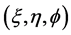 is related to the Cartesian coordinate system
is related to the Cartesian coordinate system  as follows:
as follows:
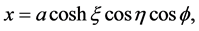 (1)
(1)
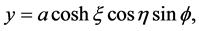 (2)
(2)
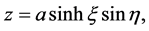 (3)
(3)
where a is the ellipse’s focal distance and this distance is one-half the ellipse’s foci such that
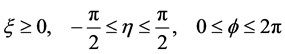 (4)
(4)
Therefore, the differential length of a line element 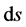 in the oblate spheroidal coordinates
in the oblate spheroidal coordinates 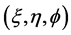 is obtained from
is obtained from
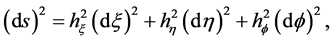 (5)
(5)
where 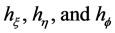 are the scale factors for the
are the scale factors for the 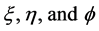 coordinates respectively. Hence, from the theory of orthogonal coordinates [8] [10] , we can write the scale factors explicitly as
coordinates respectively. Hence, from the theory of orthogonal coordinates [8] [10] , we can write the scale factors explicitly as
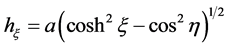 (6)
(6)
 (7)
(7)
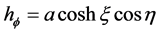 (8)
(8)
Following from Equations (1)-(3), we can define the space time position tensor in oblate spheroidal coordinate system as the set of four labelled quantity 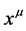 as:
as:
![]() (9)
(9)
Equation (9) can be written explicitly in terms of the coordinate axes as
![]() (10)
(10)
and in Einstein’s coordinates ![]() , where t is time coordinate and c is the speed of light in vacuum.
, where t is time coordinate and c is the speed of light in vacuum.
2.2. Metric Tensor
A fundamental quantity in Riemannian coordinate geometry is the metric tensors. Therefore the metric tensor in the oblate spheroidal coordinate system is necessary for the formulation of the Riemannian acceleration in the spheroidal coordinate system. Thus the golden metric tensor in the oblate spheroidal coordinates, ![]() , which is a covariant metric tensor of rank 2 [9] is given as follows:
, which is a covariant metric tensor of rank 2 [9] is given as follows:
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
where
![]() (16)
(16)
is the gravitational scalar potential. From Equations (11)-(15) we can obtain the corresponding contravariant metric tensors, ![]() , which is a tensor of rank 2. Therefore, by tensor transformation of Equations (11)-(15), we obtain the corresponding contravariant tensor as:
, which is a tensor of rank 2. Therefore, by tensor transformation of Equations (11)-(15), we obtain the corresponding contravariant tensor as:
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
3. Acceleration
With the metric tensors in Equations (11)-(15) and Equations (17)-(21), we can proceed to define another quantity which depends on the metric tensors. This quantity is the Christoffel’s symbols of the second kind or the coefficient of affine connections. The coefficient of affine connection or Christoffels’s symbol of the second kind is the set of labelled quantities, ![]() , given by definition [10] [11] as:
, given by definition [10] [11] as:
![]() (22)
(22)
Thus, using Equation (22), and with the metric tensors given by Equations (11)-(15) and Equations (17)-(21), we can obtain all the nonzero terms of the coefficient of affine connections. Hence, after some mathematical simplification, the non-zero terms of Equation (22) is obtained as follows:
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
and
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
and
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
and
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
and
![]() (51)
(51)
Therefore, the equations given by (23)-(51) denote all the coefficients of affine connection or Christoffel’s symbols of the second kind, where for example, ![]() denotes derivative of
denotes derivative of ![]() with respect to the coordinate axes
with respect to the coordinate axes ![]() etc.
etc.
The first rank tensor, ![]() , defined [11] in terms of the Christoffel’s symbols as:
, defined [11] in terms of the Christoffel’s symbols as:
![]() (52)
(52)
is called the Riemannian space-time or 4-dimensional “linear acceleration” tensor; ![]() and
and ![]() denote one time and two times differentiation with respect to time respectively. However, by tensor analysis [11] , the physical components of the acceleration in oblate spheroidal coordinates,
denote one time and two times differentiation with respect to time respectively. However, by tensor analysis [11] , the physical components of the acceleration in oblate spheroidal coordinates, ![]() , is given by
, is given by
![]() (53)
(53)
where
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
The Equations (54)-(57) are the physically measurable four dimensional acceleration components along the corresponding coordinate axes ![]() respectively.
respectively.
Now, substituting Equations (23)-(51) into Equation (52) and after some mathematical simplification, we can then write Equations (54)-(57) explicitly.
Consequently, Equation (54) for ![]() then becomes:
then becomes:
![]() (58)
(58)
Equation (55) for ![]() then becomes:
then becomes:
![]() (59)
(59)
Equation (56) for ![]() then becomes:
then becomes:
![]() (60)
(60)
and Equation (57) for ![]() then becomes:
then becomes:
![]() (61)
(61)
where ![]() denotes derivative of f with the coordinate axes
denotes derivative of f with the coordinate axes ![]() respectively.
respectively.
4. Results and Discussion
In this paper, we have derived the Riemannian acceleration for the oblate spheroidal coordinate system![]() . These results are presented in Equations (58)-(61) for the corresponding axes of the oblate coordinate system. The results derived for the linear acceleration vector in Equations (58)-(61) reduce to the pure
. These results are presented in Equations (58)-(61) for the corresponding axes of the oblate coordinate system. The results derived for the linear acceleration vector in Equations (58)-(61) reduce to the pure
Newtonian linear acceleration in the limit of![]() . The results derived here in Equations (58)-(61) contain post Newtonian correction terms of all orders of
. The results derived here in Equations (58)-(61) contain post Newtonian correction terms of all orders of![]() .
.