Effects of Rayleigh Number on MHD Heat Transfer and Fluid Flow in Two-Dimensional Open Square Cavity with Heat Generation ()
Received 1 December 2015; accepted 20 February 2016; published 23 February 2016

1. Introduction
The convective heat transfer and the natural convection flow with the presence of magnetic field of the fluid are of great importance in scientific and engineering research, because these types of complicated geometries have applications in engineering and industrial fields. This type of problems of heat transfer attracted very attention of researchers since its numerous uses in the areas of energy conservations, cooling of electrical and electronic equipments, design of solar collectors, heat transfer devices etc. Recently many research work have been done in this field which influence the convection flow nature. It is difficult to solve the natural convection problem in complicated geometry like it. MHD acceleration can use to develop supersonic air craft technology.
The numerical study on MHD natural convection heat transfer and fluid flow in a two-dimensional square open cavity containing a heated circular cylinder has been done. The left vertical wall is kept at A constant heat flux is set at the left vertical wall, different high and low temperature are set at bottom and top walls of the cavity and remaining side wall is open. Two dimensional Naviar Stoke’s equations with energy equation are used to govern the problem and Galerkin’s Weighted Residual Finite Element Method is used to solve the problem. In the result it is observed that all isotherm lines are concentrated at right lower corner of the cavity and the heat transfer rate is suppressed in suppressed of Rayleigh number in the cavity when Hartmann number is fixed. Recirculations are created in the flow field. Recirculation region is increasing with increasing Rayleigh number (Ra). It is a good agreement with the existing Heat Transfer Theory.
The terms magneto hydrodynamic, hydrodynamics, magneto gas dynamics and magneto aerodynamics all are the branches of fluid dynamics that deals with the motion of electrically conducting fluids in presence of electric and magnetic fields. The influence of the magnetic field on the boundary layer is exerted only through induced forces within the boundary layer itself, with no additional effects arising from free stream pressure gradient.
Literature Review
Chan and Tien [1] investigated shallow open cavities and made a comparison study using a square cavity in an enlarged computational domain. They considered a square open cavity having an isothermal vertical side facing the opening and two adjoining adiabatic horizontal sides. They found that satisfactory heat transfer results could be obtained, especially at high Rayleigh numbers. Mohammad [2] studied inclined open square cavities. He considered a restricted computational domain. The rate of change of both velocity components were set to zero at the opening plane which were different from that of Chan and Tien [1] . He found that heat transfer was not sensitive to inclination angle and the flow was unstable at high Rayleigh numbers and small inclination angles.
Ostrach [3] , Davis [4] , Hossain and Wilson [5] , Hossain et al. [6] and Sarris et al. [7] studied MHD natural convection in a laterally and volumetrically heated square cavity. Their results show that the effect of increasing Hartmann number was not found to be straight forward connected with the resulting flow patterns. Roy and Basak [8] analyzed natural convection flows in a square cavity with non-uniformly heated wall(s). S. Pervin and R. Nasrin [9] , (2011) studied MHD free convection heat transfer for different values of Rayleigh numbers Ra and Hartmann numbers Ha in a rectangular enclosure. They found that the flow pattern and temperature distributions are dependent on the used parameters. Sheikh Anwar Hossain and Alim [10] studied Effects of Natural Convection from an open square cavity containing a heated circular cylinder. S. Saha [11] studied thermo-magnetic convection and heat transfer of paramagnetic fluid in an open square cavity with different boundary conditions. His results show the Effects of Magnetic Rayleigh number, Prandtl number on the flow pattern and isotherm as well as on the heat absorption graphically. He found that the heat transfer rate is suppressed in decreased of the Magnetic Rayleigh number. Hossain, S. A. et al. [12] , (2015) studied MHD free convection heat transfer in an open square cavity containing a heated circular cylinder. In the result they found that heat transfer rate is increased in decreased Hartmann number.
The study related to heat absorption or rejection in the confined rectangular enclosures has been well discussed in the literature C. Taylor and P. Hood [13] , Chandrasekhar [14] , Dechaumphai [15] . It is observed that comparatively a little work has been done in the case of open square cavities. It might be the difficult on using the boundary conditions at the open side.
2. Two-Dimensional Model
The two-dimensional diagram of the system considered in the present study is shown in Figure 1. The model
![]()
Figure 1. Physical diagram of the problem.
consists of an open square cavity with sides of length L. A heated circular cylinder of diameter D is located at the center of the cavity. The two-dimensional Cartesian co-ordinate system with origin at the lower left corner of the computational domain is considered here. A constant heat flux q is considered at the left vertical wall of the cavity. The bottom wall is kept high temperature Th and top wall is kept at low temperature Tc. The remaining right side wall is open. The temperature at the cylinder Th1 is less than that of the bottom wall. A magnetic force of strength B0 is applied horizontally normal to the side walls.
3. Mathematical Model
The two-dimensional Naviar-Stoke’s equations together with the energy equation are used to govern the MHD natural convection heat transfer and fluid flow. In this case the flow is considered as steady, laminar, incompressible, two-dimensional and with buoyancy force. To relate the density changes to temperature changes in the fluid properties the Boussinesq approximation is used to here. The following system of differential equations can govern the steady MHD natural convection.
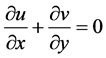 (1)
(1)
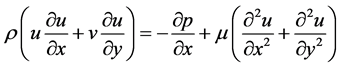 (2)
(2)
 (3)
(3)
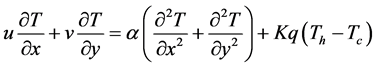 (4)
(4)
3.1. Boundary Conditions
At Bottom wall: 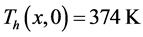
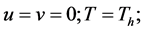 (say);
(say); 
At Top wall: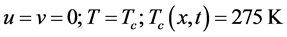 ;
; 
At the Left wall: u = v = 0, and heat flux q = 150 w/m2, 200 w/m2, p = 0.
At the right and open side: Convective Boundary Condition (CBC), pressure p = 0, u = v.
At the circular cylinder: ,
, 
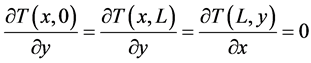
In this work x and y denote the distances measured along the bottom and vertical wall respectively from the origin; u and v denote the velocity components in the x and y direction respectively; T represents the temperature in Kelvin scale; g and a denote the kinematic viscosity and the thermal diffusivity respectively; p denotes the pressure and r is the density of the fluid in the cavity.
3.2. Governing Equations in Non-Dimensional Form
The governing equations are nondimensionalized using the following scales.
3.3. Non-Dimensional Scales
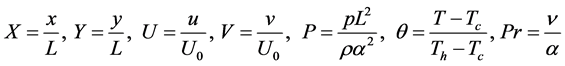
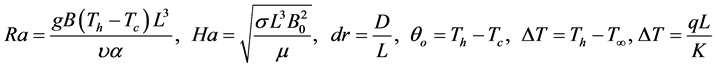
3.4. Non-Dimensional Governing Equations
Continuity equation:
![]() (5)
(5)
Momentum equations:
![]() (6)
(6)
![]() , (7)
, (7)
Energy equation:
![]() (8)
(8)
where ![]() is Prandtl number,
is Prandtl number, ![]() is Rayleigh number and
is Rayleigh number and
![]() is Hartmann number,
is Hartmann number, ![]()
3.5. Boundary Conditions
At Bottom wall:![]() .At Top wall:
.At Top wall: ![]()
At the left wall: U = V = 0; Heat Flux q = 125 w/m2, 150 w/m2, 200 w/m2, p = 0
At the right and open side: Convective Boundary Condition (CBC), p = 0.
The Nusselt number for natural convection is a function of the Grashof number only. We can obtain the local
Nusselt number Nu from the temperature field by applying the function![]() .
.
The overall or average Nusselt number was calculated by integrating the temperature gradient over the heated wall as follows:
![]()
Here Pr is a nondimensional heat transfer characteristic in the flow field of natural convection. Here Pr = 0.73.
4. Numerical Technique
The updated version of the software on Finite Element Method as numerical technique based on the Galerkin weighted residual method of finite element method is used in this study. This technique is well described by Tailor and Hood [13] and Dechaumphai [15] . In this case the solution domain is discretized into finite element meshes, which are composed of non-uniform triangular elements. Then the non-dimensional nonlinear governing partial differential equations (i.e. mass, momentum and energy equations) are transferred into a system of integral equations by applying the Galerkin weighted residual technique. To obtain the nonlinear algebraic equations Gauss’s quadrature method is used for integration over each term of these differential equations. Then these obtained nonlinear algebraic equations are modified by setting boundary conditions. Then Newton’s Method is used to transfer the nonlinear algebraic equations into linear algebraic equations. Finally, triangular factorization method is used to solve these linear equations numerically by Finite Element Method. Then numerical solution is converted into graphical solution in terms of isotherms, streamlines and line graphs. To get this results we have defined a program with boundary conditions and values of different parameters in the Finite Element Method. Then run these programs for each set of value. We accept only the convergent solutions. We shifted these graphical results from program to word file and graphical results of line graphs are presented into tabular form.
5. Results and Graphical Discussion
Computer simulation of Finite Element Method is used to perform the analysis of laminar natural convection heat transfer and fluid flow in an open square cavity with a heated circular cylinder. Effects of various Rayleigh number (Ra) with some fixed Hartmann number (Ha) and Heat flux q are studied on heat transfer and flow inside the cavity by visualizations and line Graphs. The visualizations describe the temperature distributions and flow fields by isotherms and streamlines for different parameters. The values of Ra and Ha in this study vary from 5 × 104 to 5 × 106 and 25 to 150 respectively while Pr = 0.73 & heat flux q = 125, 150, 200. The results are also presented in the tabular form.
The flow with all Ra in this work have been affected by the buoyancy force. Figures from Figure 2(a), Figure 3(a), Figure 4(a), Figure 5(a), Figure 6(a), Figure 7(a) and Figure 8(a) illustrate temperature field in the flow region and in figures from Figure 2(b), Figure 3(b), Figure 4(b), Figure 5(b), Figure 6(b), Figure 7(b) and Figure 8(b) illustrate streamlines in the flow field. The highest temperature regions remain at the lower half of the open side of the cavity in all figures excepts for Ra = 5 × 106 in Figure 7(a). The isothermal lines are nonlinear for all Ra used in this work and occupied more than right half of the region in the cavity. The all most all isothermal lines are concentrated at the right lower corner of the cavity. The area of isothermal lines and recirculations are increasing with increasing Ra in the same Ha.
Figure 2 Shows the effects of Ra = 5 × 104, 105, 5 × 105, 106, on isotherms as well as on streamlines for the present configuration at Ha = 75, q = 200. Figure 2(a) shows the highest temperature remains at the lower part of the cavity. In Figure 2(b) recirculations are formed around the cylinder. The recirculation region is increased for Ra = 5 × 105, 106.
Figure 3 shows the effects for Ra = 105, 5 × 105, 106, 5 × 106 on isotherms as well as on streamlines for the present configuration at Ha = 25, q = 125. In this case all most all isothermal lines are concentrated at the right lower corner of the cavity. Figure 3(a) shows the highest temperature at the lower part of the open side. In Figure 3(b) recirculations are formed around the cylinder and one small vortex is formed above the cylinder in the cavity for Ra = 5 × 106. The recirculations region are increased for Ra = 5 × 105, 106, 5 × 106.
Figure 4 shows the effects of Ra = 104, 5 × 104, 105, 5 × 105 on isotherms as well as on streamlines for the present configuration at Ha = 25, q = 150. In Figure 4(b) recirculations are formed around the cylinder at every Ra in the cavity. The recirculations region are increased for Ra = 105, 5 × 105. In Figure 4(a) all most all the isothermal lines are concentrated at the lower right corner of the cavity.
Figure 5 shows the effects for Ra = 105, 5 × 105, 106, 5 × 106 on isotherms as well as on streamlines for the present configuration at Ha = 75, q = 125. In Figure 5(b) recirculations are formed around the cylinder for every Ra. The recirculations regionare increased for Ra = 5 × 105, 106, 5 × 106. The isothermal lines are concentrated at the lower right corner of the cavity. One small vortex is formed above the cylinder for Ra = 5 × 106. Figure 6 shows the effects of Ra = 105, 5 × 105, 106, 5 × 106 on isotherms as well as on streamlines for the present configuration at Ha = 100, q = 125. In Figure 6(b) recirculations are formed around the cylinder at every Ra and one small vortex is formed above the cylinder for Ra = 5 × 106. The recirculations region are increased for Ra = 5 × 105, 106, 5 × 106. All most all isothermal lines are concentrated at the lower right corner of the cavity for every
![]()
Figure 2. Streamlines (a) & isotherms (b) for various Ra and Ha = 75, Pr = 0.73, q = 200 in the cavity.
![]()
Figure 3. (a) Isotherms & (b) streamlines in the cavity for various Ra and Ha = 25, q = 125.
![]()
Figure 4. (a) Isotherms and (b) streamlines for various Ra while Ha = 25 & heat flux =150.
![]()
Figure 5. (a) Isotherms and (b) streamlines for various Ra while Ha = 75 & heat flux q =150.
![]()
Figure 6. (a) Isotherms and (b) streamlines for Ra= 105, …, 5 × 106 while Ha = 100 & heat flux q = 125.
![]()
Figure 7. (a) Isotherms and (b) Streamlines for Ra = 105, … , 5 × 106 while Ha =125 & Heat flux =125.
![]()
Figure 8. (a) Isotherms and (b) streamlines for Ra= 5 × 104, … , 106 while Ha =100 & heat flux = 250.
Ra.
Figure 7 shows the effects of Ra = 105, 5 × 105, 106, 5 × 106 at Ha = 125 and heat flux q = 125. The isotherm lines are concentrated at right lower corner of the cavity for every Ra and the isotherm lines are located in the right half of the cavity. Here recirculations are formed around the cylinder for every Ha. One small vortex is formed above the cylinder for Ra = 5 × 106. The recirculations region are increased for Ra = 5 × 105, 106, 5 × 106. The isothermal lines are concentrated at the lower right corner of the cavity for every Ra. Here the highest temperature remains at upper half of the open side for Ra = 5 × 106 and Ha = 125.
Figure 8 Show the effects for Ra = 5 × 104, 105, 5 × 105, 106 on isotherms as well as on streamlines for the present configuration at Ha = 100, q = 250. Here isotherm lines concentrate at lower right corner of the cavity for every Ra. Here recirculations are formed around the cylinder for every Ra. The recirculation regions are increased for Ra = 5 × 105, 106. Table 1 shows the amount of heat transferred at the top wall, cylinder and open side of the cavity respectively for various Rayleigh numbers Ra.
The various Raleigh numbers and magnetic force affect the heat flux along the sides of the cavity. These are observed in figures from Figure 9 and Figure 10 that Raleigh number affect on heat flux proportionately. That is heat flux is maximum when Ra is maximum at the top wall and open side. That is if Ra rises then heat flux increases at the open side and upper side of the cavity. But Figure 11 shows that the heat transfer at the cylinder is increasing for Ra = 5 × 104 to 5 × 105 and decreasing for Ra = 106 to 5 × 106.
![]()
Figure 9. Line graph of heat flux at upper wall for Ra = 5 × 104, 105, 5 × 105, 106 & Ha = 80, q = 125.
![]()
Figure 10. Line graph of heat flux at the open side for Ha = 80, Ra = 5 × 104, 105, 5 × 105, 106, q = 125, Pr = 0.73.
![]()
Figure 11. Line graph of heat flux at the cylinder for Ha = 80, Ra = 5 × 104, 105, 5 × 105,. 5 × 106, q = 125.
![]()
Table 1. Heat transfer at the top wall, cylinder and open side respectively for various Ra while Ha = 80 and q = 125.
6. Conclusions
The numerical study on MHD natural convection heat transfer and fluid flow in a two-dimensional square open cavity containing a heated circular cylinder has been done.
The flow with all Ra in this work has been affected by the buoyancy force. Temperature fields are illustrated in the flow region.
The high temperature region remains at the lower half of the open side for all Ra except for Ra = 5 × 106 in Figure 7(a).
The isothermal lines are nonlinear for all Ra used in this work and they occupied more than right half region of the cavity.
The significant findings of this work are that for all cases of Ha and Ra the isothermal lines concentrated to the right lower corner of the cavity and there are recirculations around the cylinder and one small vortex has been created above the cylinder in the cavity for highest Ra.
The heat transfer is increasing with increasing Ra at top wall and open side of the cavity.
The recirculation region is increasing with increasing Ra.
The result of this work is a good agreement with the existing heat transfer theory.
Nomenclature