Acoustic Characteristics Analysis of Industrial Premises with Process Equipment ()

1. Introduction
Repeated calculations of noise power parameters are made at a choice of building-acoustic measures for noise abatement in industrial premises and estimation of their efficiency. The validity of calculations depends on a degree of the count of actual conditions of reflected sound fields’ formation. The energy parameters of a reflected field essentially depend on presence in premises of process equipment and other subjects, falling on which sound waves are dispersed in premise space generally by probabilistic mode. Dissipation of sound energy leads to change of acoustic parameters of a premise: a mean length of free runs of sound waves, reverberation time and mean sound absorption factor. Failure to take account of the data of circumstances can call essential errors at determination of sound pressure levels and estimation of efficiency of building-acoustic measures of noise abatement, and in particular, sound-absorbing linings.
2. Methodology and Program of Calculation
For the estimation of processing equipment effect on acoustic parameters of a premise a computer program was designed according to the principles of the ray tracing method [1]. The program consists of separate independent modules, combining which it is possible to model acoustic processes in premises with different acoustic properties.
Designing the module for the calculation of the mean length of the sound rays’ free runs it was taken into account, that the energy of rays does not remain constant in actual premises; it reduces at each reflection from surfaces. Therefore, there are simultaneously in a premise rays with large values of portable energy, which determine the main energy contribution to the formation of the reflected sound field, and rays with a small quantity of energy, inessential influencing the power characteristics of the field. Considering this fact as well as the presence of the process equipment, which raises a degree of the direction contingency of reflected sound rays, it is provided in the program the capability of determination of the mean length of rays’ free runs with the use of the sound reflection model on the basis of Lambert’s law and with regard to their actual power condition. The methodology of such approach is as follows.
The sound field in a premise seems to consist of a plurality of rays with free run lengths 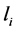 and corresponding portable powers
and corresponding portable powers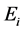 . The further the path of a ray is being traced, the less significant the power contribution of this ray is. The criterion for the tracking termination of the ray path is the fixed reducing its power relative to the original one. So, the power characteristics of the rays can act as weight factors in determining the mean length of the rays’ free run. For this purpose the full range of possible lengths of the rays’ free runs{lmin ÷ lmax} can be split into M = [(lmax − lmin)/Δl] segments (lmax and lmin are the most and the least available lengths of the rays’ free runs, for example for the diagonal and the minimal size of a premise). Distributing the total power of the sound field according to the corresponding segments one can get a histogram of the lengths of the rays’ free runs distribution with regard to their energy balance
. The further the path of a ray is being traced, the less significant the power contribution of this ray is. The criterion for the tracking termination of the ray path is the fixed reducing its power relative to the original one. So, the power characteristics of the rays can act as weight factors in determining the mean length of the rays’ free run. For this purpose the full range of possible lengths of the rays’ free runs{lmin ÷ lmax} can be split into M = [(lmax − lmin)/Δl] segments (lmax and lmin are the most and the least available lengths of the rays’ free runs, for example for the diagonal and the minimal size of a premise). Distributing the total power of the sound field according to the corresponding segments one can get a histogram of the lengths of the rays’ free runs distribution with regard to their energy balance
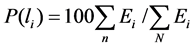 , (1)
, (1)
where n is the number of rays that fall within the range of the mean free path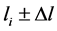 ; N is the overall quantity of the rays being observed.
; N is the overall quantity of the rays being observed.
The mean value of the free run lengths 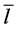 based on this distribution is
based on this distribution is
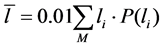 . (2)
. (2)
The reverberation time T is also determined in the module on the basis of the calculation of the reflected sound field power parameters after switching-off a noise source and evaluating the decay time of reflected power on 60 dB concerning an initial level.
The received items of information on a mean free run length and reverberation time enable to determine a mean sound absorption factor 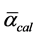 of the premise, using the well-known Airing’s formula as
of the premise, using the well-known Airing’s formula as
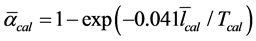 , (3)
, (3)
where 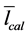 is the mean length of the ray’s free runs in a premise with scatterers, m, determined in the program with the allowance of the power significance of the rays;
is the mean length of the ray’s free runs in a premise with scatterers, m, determined in the program with the allowance of the power significance of the rays; 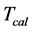 is the reverberation time in a premise with scatterers, s, calculated in the program.
is the reverberation time in a premise with scatterers, s, calculated in the program.
The program was utilized to estimate the process equipment influence on the acoustic parameters of industrial premises. As an example the findings of the research in the flat industrial premise dimensioned 36 × 36 × 6 m are presented below. 81 scatterers each sizing 1.5 × 1.5 × 1.5 m are placed in the premise filled uniformly all area of the floor concerning symmetrically its center with spacing interval between the adjacent scatterers equal to 2.0 m . The sound absorption factors of the walls aw and of the floor afl were taken equal to 0.02, and of the scatterers surfaces asc equal to 0.05. The sound absorption factor of the ceiling aseil was being changed from 0.02 up to 0.90. The sound reflection from the surfaces was received as diffusing and corresponded to the Lambert’s law. The non-directed sound source was placed in the center of the premise. Atsimulation 30,000 rays were tracked in each case.
3. Estimation of Mean Length of Sound Rays’ Free Runs
The calculations of mean lengths of the rays’ free runs were executed for the above premise with the scatterers and for the empty premise. At the last case the Sabin’s formula was used also, which do not take into account the power significance of separate rays:
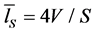 , (4)
, (4)
where V and S are the volume, m3, and the limiting surfaces’ area, m2, of the premise.
The plots of mean length of the rays’ free run 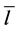 versus the ceiling sound absorption factor aseil are given in Figure 1.
versus the ceiling sound absorption factor aseil are given in Figure 1.
The growth of the mean length of the rays’ free runs 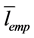 at the increase of the sound absorption factor of the ceiling is seen for the empty premise. It may be connected with the degeneration of oblique rays falling more often on the ceiling surface and with the increase of the power significance of tangent and axial rays, which are not falling on the sound-absorbing surface of the ceiling.
at the increase of the sound absorption factor of the ceiling is seen for the empty premise. It may be connected with the degeneration of oblique rays falling more often on the ceiling surface and with the increase of the power significance of tangent and axial rays, which are not falling on the sound-absorbing surface of the ceiling.
At the same time the presence of scatterers reduces the mean length of rays’ free runs 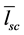 sharply. In addition
sharply. In addition 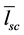 insignificantly depends on the ceiling sound absorption aseil. Apparently, it is associated with the fact that the main power is carried by the rays distributing within the space between scatterers. It is established that in this case at aseil < 0.50 the outcomes well matched with
insignificantly depends on the ceiling sound absorption aseil. Apparently, it is associated with the fact that the main power is carried by the rays distributing within the space between scatterers. It is established that in this case at aseil < 0.50 the outcomes well matched with 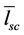 are given by using the Sabin’s formula with taking into account the presence of scatterers in the premise:
are given by using the Sabin’s formula with taking into account the presence of scatterers in the premise:
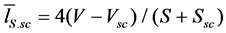 , (5)
, (5)
where Vsc, Ssc are the general volume, m3, and the total area, m2, of scatterers located in a premise.
4. Estimation of Reverberation Time
The findings of investigation of the reverberation time are shown in Figure 2. The outcomes of reverberation time calculations Tcal obtained by the ray tracing method are given and the data of calculations executed according to Airing’s formula with usage of mean length of rays’ free runs obtained from Equations (4) and (5):
![]() , (6)
, (6)
![]() . (7)
. (7)
The mean acoustic absorption factor of the premise ![]() was calculated by the equation
was calculated by the equation
![]() , (8)
, (8)
where ai, Si are the acoustic absorption factor and area, m2, of the i-th limiting surface of a premise; asc, Ssc are the acoustic absorption factor and the general area, m2, of scatterers surfaces; Stot is the total area of limiting surfaces , m2,of a premise and scatterers.
The calculations under Equation (7) are well agreed with the outcomes of computer simulation. At the same time the calculations under Equation (6), which is usually used in practice, differ essentially from outcomes of simulation in the premise without sound-absorbing lining and coincide practically with them if the premise has the muffled ceiling.
The divergences of the reverberation time, calculated by Equation (6), and outcomes of simulation indicate one practically relevant circumstance that is concerned with an estimation of the sound absorption of the equipment placed in the premise. It is considered, that the actual sound absorption of the equipment as a whole is much higher than the sound absorption of separate metallic surfaces of the equipment [2]. Such conclusions are grounded on the calculation outcomes of the mean acoustic absorption factor in the premise with usage of the reverberation time Tmeas to be received experimentally. In this case the mean sound absorption factor ![]() is determined according to Airing’s formula as
is determined according to Airing’s formula as
![]() . (9)
. (9)
As ![]() is much more, than
is much more, than ![]() (see Figure 1), the values of
(see Figure 1), the values of![]() , received according to Equation (9), can
, received according to Equation (9), can
![]()
Figure 1. Change of the mean length of ray free run in the flat premise depending on the ceiling sound absorption.
![]()
Figure 2. Change of the reverberation time in the premise depending on the ceiling sound absorption.
rather essentially exceed values of ![]() determined by Equation (8).
determined by Equation (8).
Substituting the value of ![]() in Equation (8) instead of
in Equation (8) instead of![]() , it is possible to receive value
, it is possible to receive value ![]() with taking into account an apparent extra sound absorption, caused by reductions of the mean length of rays’ free runs due to presence scatterers in a premise, that is neglected by using Equation (9).
with taking into account an apparent extra sound absorption, caused by reductions of the mean length of rays’ free runs due to presence scatterers in a premise, that is neglected by using Equation (9).
The values of![]() , received for the considered flat premise are shown in Figure 3. At that the values of Tcal calculated by ray tracing method were used as Tmeas in Equation (9). It is visible, that the values
, received for the considered flat premise are shown in Figure 3. At that the values of Tcal calculated by ray tracing method were used as Tmeas in Equation (9). It is visible, that the values ![]() considerably exceed actual values
considerably exceed actual values ![]() = 0.05 utilized at calculations. At the same time they are agreed with the data indicated in [2], which were obtained experimentally for production equipment, placed in industrial premises.
= 0.05 utilized at calculations. At the same time they are agreed with the data indicated in [2], which were obtained experimentally for production equipment, placed in industrial premises.
![]()
Figure 3. Change of sound absorption factor of scatterers depending on ceiling sound absorption.
5. Conclusion
The obtained outcomes of researches of the acoustic parameters changes at placing scatterers in premises make it possible to consider that the computer simulation of the reflected field formation processes on the basis of the ray tracing method with taking into account the rays’ portable energy is an effective way of the noise condition analysis in actual industrial premises. It allows determining objectively the integral acoustic characteristics of industrial premises, considering the influence of premise parameters, the presence of the sound-disseminating equipment and its characteristics, as well as other factors significant for the distribution of the reflected sound power. With the help of this it is possible to clarify the engineering formulas being in use.