Received 12 November 2015; accepted 28 December 2015; published 31 December 2015

1. Introduction
A deformed quantum mechanics with a generalized Heisenberg Uncertainty (GUP) has been introduced by Kemp et al. [1] [2] . As a consequence, there exist smallest distance limitations in spacetime, known as minimal lengths. This minimal lengths change quantum mechanics that have been established. As an example, there has been calculated Schrodinger equation in the presence of minimal length [3] [4] , the effect of the minimal length on the energy spectrum of Coulomb potential [5] [6] , Casimir effect [7] -[10] , and Dirac Oscillator [11] -[14] .
The minimum length also affects the quantum thermodynamics, quantum generalization of the classical thermodynamics, for instance, quantum heat engine. In the quantum thermodynamics, there is isoenergetic process that is analogous to the isothermal process; and isoentropic process that is analogous to adiabatic process in classical thermodynamics. The cycle composed of two isoenergetic and two isoentropic trajectories is called isoenergetic cycle [15] . The efficiency of quantum heat engine has been calculated in [15] -[17] . The results show that the efficiency depends only on the expansion parameter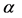 .
.
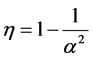 (1)
(1)
The point is that the width of the potential well has no effect on the value of efficiency. In this paper, we compute the effect of the minimum length on the quantum heat engine efficiency.
This paper is organized as follows. In Section 2 we derive quantized particle energy in infinite one-dimen- sional potential well in the presence of minimal length. In Section 3 we determine inward and outward heat through the system by isoenergetic and isoentropic process, and then we compute the efficiency of Carnot Quantum heat engine with two-level state. Finally, in Section 4 we present a discussion of our results and our conclusions.
2. Schrodinger Equation with Minimal Length
The general form one-dimensional Schrodinger equation is as follows
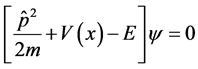 (2)
(2)
with operator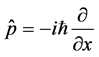 . In order to incorporate minimal lengths in our equation, we used literature [3] about the position space representations as follows
. In order to incorporate minimal lengths in our equation, we used literature [3] about the position space representations as follows
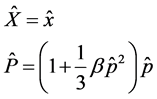 (3)
(3)
where 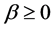 is a small parameter. With the representation above, we obtain Schrodinger equation with minimal lengths as follows
is a small parameter. With the representation above, we obtain Schrodinger equation with minimal lengths as follows
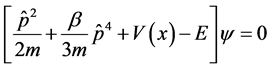 (4)
(4)
We choose one-dimensional infinite potential well as a simple model, with potential energy
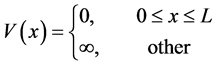 (5)
(5)
So, particle in potential well can be described by one-dimensional time independent Schrodinger as follows
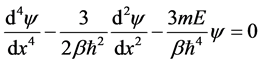 (6)
(6)
The equation can be solved by first determine the roots of equation
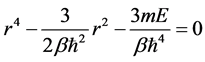 (7)
(7)
And we get
 (8)
(8)
We only have two boundary condition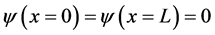 . It is impossible to find solutions of the equation by using all four roots. So, in order to obtain exact energy particle that can be applied to boundary conditions, we only use two roots. Then we propose the solution as follows
. It is impossible to find solutions of the equation by using all four roots. So, in order to obtain exact energy particle that can be applied to boundary conditions, we only use two roots. Then we propose the solution as follows
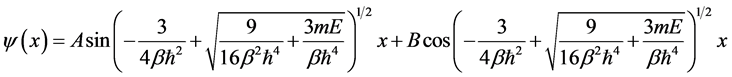 (9)
(9)
By applying the boundary conditions and nornalization condition, we obtain quantized wave functions as follows
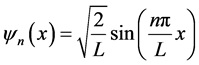 (10)
(10)
and energy
![]() (11)
(11)
which when we take![]() , we have ordinary quantized energy in infinite one-dimensional potential well without minimal length
, we have ordinary quantized energy in infinite one-dimensional potential well without minimal length
![]() (12)
(12)
3. Isoenergetic Cycle Process with Minimum Length
The system is assumed to be driven by reversible quasi-static process. That means the wall is moved very slowly by an applied external forced [15] . Because we work on quantum thermodynamics, it is necessary to introduced the ensemble average energy of the system as
![]() (13)
(13)
The change of the energy during the moving is given by
![]() (14)
(14)
The above equation is analogous to the first law of thermodynamics. The term ![]() analogous to internal energy,
analogous to internal energy, ![]() analogous to heat exchanged, and
analogous to heat exchanged, and ![]() to the work done.
to the work done.
For practical reason, we choose the system with two-level energy state![]() . The Carnot cycle is shown as Figure 1.
. The Carnot cycle is shown as Figure 1.
Let us consider first the isoenergetic process. The isoenergetic process analogous to isothermal process in classical thermodynamics, so![]() . According to reference [15] , the heat exchanged along trajectory
. According to reference [15] , the heat exchanged along trajectory ![]() to
to ![]() given by
given by
![]() (15)
(15)
Because the initial state entirely to ![]() and final state entirely to
and final state entirely to ![]() then we get relation as follows
then we get relation as follows
![]()
Figure 1. Carnot circle for two-level system.
![]() (16)
(16)
By using (11), we get
![]() (17)
(17)
As noted earlier, that during the isoenergetic process, the total energy remains constant. Then we get![]() , that makes
, that makes![]() . So during the first isoenergetic process, the heat flows from environment to system with
. So during the first isoenergetic process, the heat flows from environment to system with
![]() (18)
(18)
The work done to the system, can be obtain by![]() .
.
At the second, we arrive at isoentropic process. For isoentropic process, the probability is unchanged through von Neumann entropy
![]() (19)
(19)
The heat exchange during isoentropic process equal to zero. As a Figure 1, we expand the width of the potential well, from ![]() to
to![]() . If the width of the potential well is changed, then so does the total energy. Which means that it is not necessary to change the quantum state of the system during the isoentropic process, the state still on
. If the width of the potential well is changed, then so does the total energy. Which means that it is not necessary to change the quantum state of the system during the isoentropic process, the state still on![]() . So the work can be calculated as follows
. So the work can be calculated as follows
![]() (20)
(20)
Similar with isoenergetic process, we can calculate the heat exchanged from ![]() to
to![]() . The heat exchanged from the system to the environment along this process is given by
. The heat exchanged from the system to the environment along this process is given by
![]() (21)
(21)
The last path along the cycle is isoentropic process, which return fully to the initial condition. The work performed during this process from ![]() to
to ![]() is given by
is given by
![]() (22)
(22)
We obtain that work along two isoentropic process cancel each other, that is![]() . Therefore, the efficiency of the cycle can be expressed by
. Therefore, the efficiency of the cycle can be expressed by
![]() (23)
(23)
By substituting Equation (18) and Equation (21), we obtain the explicit analytical expression
![]() (24)
(24)
with
![]() (25)
(25)
Then we plot the graph between the efficiency versus the width of potential as Figure 2. From Figure 2, we obtain that the efficiency value depends on the initial value of potential width. We get interesting result that the efficiency value increase above classical result with the decreasing the width of potential. The efficiency is also affected by the size of minimal length. If we approximate![]() , the value of efficiency (24) would be
, the value of efficiency (24) would be
![]() (26)
(26)
And at large width of potential well, the efficiency value approaches classical result.
At Figure 3, we plot the graph with ![]() variations. We take
variations. We take ![]() and using L’hopital theorem, we get
and using L’hopital theorem, we get
![]()
Figure 2. The efficiency versus initial potential width, with ![]() and
and ![]() variations.
variations.
![]()
Figure 3. The efficiency versus initial potential width, with ![]() and
and ![]() variations.
variations.
Schrodinger limit as
![]() (27)
(27)
Efficiency value returns to the quantum engine efficiency without the presence of minimal length.
4. Discussion and Conclusion
In this work, we have studied the consequences of the minimal length on the quantum thermodynamics. This minimal length modifies Schrodinger equation to be fourth order differential equation. We choose periodic solutions in order to obtain the exact solutions. After that, we calculate the efficiency of heat engine with procedure in Reference [15] . We obtain for the width of potential smaller than![]() , the efficiency as (26). But for the width greater than
, the efficiency as (26). But for the width greater than![]() , the efficiency approaches to classical result (27).
, the efficiency approaches to classical result (27).
We conclude that the minimal length affects the efficiency of the quantum heat engine at small size of potential well. This effect can be explained by considering the particle as a ball-point having a finite size which is of order of the minimal length [1] .
Acknowledgements
This work is supported by LPPM ITS.