A Stock-Recruitment Relationship Applicable to Pacific Bluefin Tuna and the Pacific Stock of Japanese Sardine ()
Received 30 September 2015; accepted 20 December 2015; published 23 December 2015

1. Introduction
Recently, the abundance of Pacific bluefin tuna, Thunnus thynnus, has decreased and it is necessary to rehabilitate the stock [1] . In order to discuss management procedure, it is important to know the stock-recruitment relationship (SRR) for this species; however, clear relationship between recruitment (R) and spawning stock biomass (S) has not been detected, and the recruitment seems to distribute regardless of the level of the S. If the relationship between R and S does not clearly detected, an increase of S seems to be ineffective in the management procedure, and the main purpose of the management is to manage the recruited population.
That is, a shape or a model of SRR is one of the key issues to elucidate when we discuss a management procedure. The Ricker [2] , Beverton and Holt [3] or hockey stick [4] model has been used as a typical SRR model in fisheries sciences. A huge number of papers related to SRR have been published; however, almost all papers have been discussed based on the assumption that a density-dependent effect really exists [5] -[8] .
Recently, however, Sakuramoto [9] -[11] proposed a new SRR model that incorporated environmental factors instead of assuming a density-dependent effect. That is,
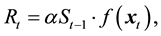 (1)
(1)
where Rt and St−1 denote the recruitment in year t and spawning stock biomass in year t − 1, and f(.) denotes a function that evaluates the effects of environmental factors in year t. The variable  is a vector
is a vector
representing the environmental factors, comprised not only of physical factors such as water temperature, but also biological interactions such as prey-predator relationships. Parameters α and k denote a proportional constant and the number of environmental factors, respectively. That is, Rt is proportionally determined by St−1, and simultaneously, Rt is affected by environmental factors in year t.
The purpose of this study is to determine whether the SRR model proposed for the Pacific stock of Japanese sardine [9] -[11] is also applicable for Pacific bluefin tuna. That is, we investigated whether the mechanism in SRR for Pacific bluefin tuna and that in the Pacific stock of Japanese sardine can be expressed by the same concept shown in Equation (1). Further, this paper explores the revised concept of SRR that exists behind the observed SRR.
2. Methods
2.1. Data
For Pacific bluefin tuna, data of recruitment and spawning stock biomass from 1952 to 2012 were used [1] . For the Pacific stock of Japanese sardine, data of recruitment and spawning stock biomass from 1951 to 2012 were used [12] [13] . The index of Arctic Oscillation (AO) by month and Pacific Decadal Oscillation (PDO) by month from 1951 to 2012 were obtained from the NOAA Climate Prediction Center [14] .
2.2. Simulation Models
The following four models were assumed, based on Equation (1):
Model 1 is the basic SRR model, which is the case when environmental effects can be neglected. That is, f(xt) in Equation (1) can be assumed to be unity. That is,
 , (2)
, (2)
where α denotes the recruitment per spawning stock biomass (RPS). The survival process is expressed by
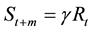 . (3)
. (3)
For simplicity, m denotes the age at maturity and longevity of the fish. That is, fish reach maturity at age m; then, they spawn their eggs and die. In Equation (3),  denotes the survival rate during m years or the spawning stock biomass per recruitment (SPR), i.e.,
denotes the survival rate during m years or the spawning stock biomass per recruitment (SPR), i.e.,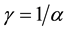 . Therefore, when the population reproduces according to Model 1, Rt and St+m are constant regardless of year.
. Therefore, when the population reproduces according to Model 1, Rt and St+m are constant regardless of year.
Model 2 is the case in which when f(xt) in Equation (1) can be expressed by 1 + r. That is,
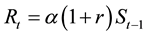 . (4)
. (4)
The increasing or decreasing rate, r, is determined by environmental factors. When environmental factors are good for the stock, r takes positive values (r > 0) and R increases. On the contrary, when environmental factors are bad for the stock, r takes negative values (−1 < r < 0) and R decreases. In this model, the survival process is the same of that shown in Equation (3).
Model 3 is the case when r in Equation (4) changes cyclically. It can be expressed by a sine curve as defined below:
 (5)
(5)
Thus,
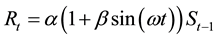 . (6)
. (6)
Here, 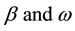 denote the amplitude of the sine curve and angular velocity, respectively. In this model, the survival rate γ is determined in order that the R and S have no trends for years. That is, γ is slightly different from 1/α. In this paper, this modified value is denoted by
denote the amplitude of the sine curve and angular velocity, respectively. In this model, the survival rate γ is determined in order that the R and S have no trends for years. That is, γ is slightly different from 1/α. In this paper, this modified value is denoted by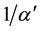 .
.
Model 4 is the case when Model 2 and Model 3 are combined: i.e., f(xt) in Equation (1) changes cyclically with an increasing or decreasing trend. That is,
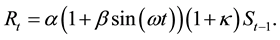 (7)
(7)
Here,  denotes the trend in R that continues throughout the period of simulation. In this model, the same survival process in Model 3 is used.
denotes the trend in R that continues throughout the period of simulation. In this model, the same survival process in Model 3 is used.
Figure 1 shows the flow from  to
to![]() , from
, from ![]() to
to![]() , and from
, and from ![]() to
to![]() , ×××, for the cases of Models 2 and 3, respectively.
, ×××, for the cases of Models 2 and 3, respectively.
2.3. Parameter Values Assumed in the Simulations
In Model 3, the values of α, ![]() are set at 5, 0.5 and π/10, respectively. That is, the cycle of this sine curve is 20 years. The length of the simulations was 60 years or 3 complete cycles. The age at maturity were set at m = 1, 2, 3 … up to 19, respectively. In model 3, γ was determined not to have any trend for R and S. The value of γ was set at 0.213, which was slightly larger than 1/α = 0.2. The initial value of S was set at 300. In model 4,
are set at 5, 0.5 and π/10, respectively. That is, the cycle of this sine curve is 20 years. The length of the simulations was 60 years or 3 complete cycles. The age at maturity were set at m = 1, 2, 3 … up to 19, respectively. In model 3, γ was determined not to have any trend for R and S. The value of γ was set at 0.213, which was slightly larger than 1/α = 0.2. The initial value of S was set at 300. In model 4, ![]() was set at 0.10, which corresponds to the 0.05 annual rate of increase when m = 2. In these simulations, for a technical reason, R and S were calculated for 100 years, and then the calculated values from the 21st to 80th years were plotted because the first year of S calculated in the simulation differs depending on the age at maturity assumed.
was set at 0.10, which corresponds to the 0.05 annual rate of increase when m = 2. In these simulations, for a technical reason, R and S were calculated for 100 years, and then the calculated values from the 21st to 80th years were plotted because the first year of S calculated in the simulation differs depending on the age at maturity assumed.
![]()
Figure 1. Stock-recruitment relationship and survival process. S in the (t − 1)-th generation produces the R in the t-th generation, and the R in the t-th generation produces the S in the (t + m)-th generation, and so on. Illustrations show the cases for Model 2 and 3, respectively.
3. Results
3.1. Relationship between R, S and Environmental Factors for Pacific Bluefin Tuna
Figure 2(a) shows the plot of the natural logarithm of Rt, ln(Rt), against that of spawning stock biomass, ln(St−1), for Pacific bluefin tuna. The plots widely scatter and it seems difficult to find any relationship between ln(Rt)
![]()
![]()
![]()
Figure 2. Stock-recruitment relationship for Pacific bluefin tuna. ln(R) and ln(S) denote the natural logarithm of recruitment in year t and that of spawning stock biomass in year t − 1, respectively. (a) 1953-2012; (b) 1956-1977; (c) 1989-1995 and 2000-2011.
![]()
![]()
Figure 3. Result of principle component analysis. The variables used were ln(R), ln(S), Arctic Oscillation by month from January to December (am, m = 1, 2, ..., 12) and the Pacific Decadal Oscillation by month from January to December (pm, m = 1, 2, ..., 12). (a) Pacific bluefin tuna; (b) Pacific stock of Japanese sardine.
and ln(St−1). However, this apparent lack of relationship is caused by the wrong approach, as Sakuramoto pointed out [11] . That is, the actual relationship between ln(Rt) and ln(St−1) should be expressed by a 3- or more than 3-dimensional model as expressed in Equation (1).
Figure 3(a) shows the result of a principle component analysis using the data of ln(R), ln(S), Arctic Oscillation by month (AO) and the Pacific Decadal Oscillation by month (PDO). In this study, only AO and PDO were used as environmental factors for the first step of an analysis. There must be many more important environmental factors that more seriously affect the dynamics of the fluctuations. However, the main purpose of this study is not to identify the most important environmental factors, but to elucidate the significant way in which environmental factors contribute to the fluctuation mechanisms in SRR.
The result of a principle component analysis showed that AO in June was located at the nearest point to that of ln(R). Hereafter, I will show the results when AO in June is used as a representative of the environmental factors. ln(S) was nearly located to ln(R) next to AO in June, July and November.
Figure 4(a) shows the trajectories of AO in June, ln(R) and ln(S) of Pacific bluefin tuna, respectively. The orange broken lines show the 3-year moving average of those values, respectively. Figure 3(a) shows that the
![]()
Figure 4. Trajectories of Arctic Oscillation or Pacific Decadal Oscillation, and ln(R) and ln(S). The orange broken line in each panel indicates a 3-year moving average for each variable. The horizontal line denotes the average of the variable. (a) Pacific bluefin tuna; (b) Pacific stock of Japanese sardine. AO6 and PDO6 denote the Arctic Oscillation in June and Pacific Decadal Oscillation in June, respectively.
high values in recruitment from 1953 to 1956 correspond to the high values in SSB from 1958 to 1961. However, a great reduction in R in 1958 and 1959 caused the reduction in SSB that began from around 1963. That is, the trajectory in ln(S) follows that in ln(R) with about 5-year lag, because the maturity age of Pacific bluefin tuna is 5 years and older.
ln(R) decreased greatly from 1957 to 1959 according to the drastic reduction of AO in June from 1957 to 1958. However, ln(R) increased greatly from 1960 to 1963 according to the great increases of the values of AO in June from 1959 to 1962. That is, the recruitment was strongly affected by environmental factors.
Figure 5(a) shows the 3-dimensional plot when the 3-year moving average of ln(R) is plotted against those of
ln(S) and AO in June. Figure 5(a) shows some relationship among those values; however, the relationship is not clear because so many data are plotted. The same plots were redrawn using shorter periods (Figures 5(b)-(f)). Figures 5(b)-(f) show the comparison between the 3-demensional plot and those for 2-demensional ones in each shorter period. For instance, Figure 5(b) shows the case when 1955 to 1965 are plotted. In this case, the 3-year moving average of ln(R) decreased as that of AO in June decreased, and the 3-year moving average of ln(R) increased as that of AO in June increased. However, 2-demensional plot of ln(R) against ln(S) did not show an density-dependent phenomenon and the 2-demensional plot of ln(R) against AO in June (AO6) showed that ln(R) changed in response to the values of AO6. This tendency can be seen for all other shorter periods. Figures 5(a)-(f) show us an essentially important fact. That is, the environmental factors should not be treated only as a random error term, but they should be treated as the main important factors that control the fluctuation in recruitment.
3.2. Relationship between R, S and Environmental Factors for the Pacific Stock of Japanese Sardine
Figure 3(b) shows the results of a principle component analysis using the data of ln(R), ln(S), AO by month and PDO by month. The result of the principle component analysis showed that, in the case of Japanese sardines, ln(R) and ln(S) landed at almost the same place on the plot. The environmental factor PDO in June was located at the nearest point to that of ln(R). Hereafter, the results of PDO in June are used as a representative of the environmental factors.
Figure 4(b) shows the trajectories of PDO in June, ln(R) and ln(S) for the Pacific stock of Japanese sardine, respectively. The orange broken lines show the 3-year moving average values of PDO in June, ln(R) and ln(S), respectively. In this case the trajectory of ln(S) follows that of ln(R) with a 2-year lag because the maturity age of the Pacific stock of Japanese sardine is 2 years and older. Figure 5(g) shows the 3-dimensional plot when ln(R) is plotted against ln(S) and PDO in June. In the case of the Japanese sardine, ln(R) showed a clear increasing trend as ln(S) and PDO in June increased.
3.3. Results of Simulations
Figure 6(a) shows the results of simulations when Model 3 is used under the assumption that the cycle of the sine curve is set at 20 years and the age of maturity is 2 years. That is, the year of maturity (m) is much less than the half-cycle of the fluctuation (m < 10). Figure 6(a) shows the trajectories of ln(R) and ln(S). In this case the age at maturity is 2 years; then, the trajectory of ln(S) follows that of ln(R) with 2-year lag. Figure 6(b) shows the SRR in this case. The SRR model assumed in the simulation was that Rt was proportionally determined by St−1; however, the apparent SRR showed three similar-shape clockwise loops increasing in size. The overall slope of the regression line was less than unity in response to the cyclic environmental factors (Table 1). Figure 6(c) and Figure 6(d) show the case when the maturity age was set at 13 years. In Figure 6(d), the apparent SRR shows widely scattered mainly anticlockwise loops of which the slope of the regression line was not significantly different from zero (Table 1).
Table 1 summarizes the slopes of the regression lines and the directions of the SRR trajectories when Model 3 was adopted with different maturity ages of 1, 2, 3 up to 19 years, respectively. Table 1 shows that when the maturity age was less than or equal to 4, the clockwise increasing loops emerged. When the maturity age was 5 or 6 years, the SRR trajectories were clockwise, but the slopes of the regression lines were not different from zero. When the maturity age was 7 or 8 years, both clockwise and anticlockwise loops emerged, and the slopes of the regression lines showed decreasing trends. When the maturity age was 9 to 13 years, both clockwise and
![]()
Table 1. Slopes of the regression lines and the directions of the SRR trajectories when Model 3 was adopted with maturity ages set at 1, 2, 3, … up to 19 years, respectively. The slopes of those for the Pacific stock of Japanese sardine and Pacific bluefin tuna are also shown.
anticlockwise loops or mainly anticlockwise loops emerged; however, the slopes of the regression lines were not different from zero. When the maturity age was greater than or equal to 14 years, all the SRR trajectories showed increasing anticlockwise loops.
For the case of Model 2, the SRR shows a very simple pattern. When r is positive, SRR shows a line of which the slope is unity and the intercept is![]() ; when r is negative, SRR shows a line of which the slope is unity and the intercept is
; when r is negative, SRR shows a line of which the slope is unity and the intercept is![]() . Here,
. Here, ![]() denotes the absolute value of r. That is, SRR shows two parallel lines above and below the baseline of which the slope is unity and the intercept is ln(α).
denotes the absolute value of r. That is, SRR shows two parallel lines above and below the baseline of which the slope is unity and the intercept is ln(α).
3.4. Comparison of Observed SRRs with Those Derived from Simulations
Figure 7(a) shows the results of simulations when Model 4 is used with the maturity age set at 2 years. When R increased by 5% per year, the apparent SRR showed three clockwise loops increasing in size. When R decreased, the result was the opposite: i.e., the apparent SRR showed three clockwise loops decreasing in size. The numbers of loops are determined by the length of the cycle and the years tested in the simulation. Figure 7(b) shows the SRR for the Pacific stock of Japanese sardine. In this case, the plots of ln(R) against ln(S) showed three clockwise loops increasing in size; however, the overall slope of the regression line was less than unity (Table 1). This SRR shape and the estimated slope coincided well with those derived from the simulation when the maturity age was set at 2 years.
Figure 2(a) shows the stock-recruitment relationship for Pacific bluefin tuna. In this case, the plots of ln(R) against ln(S) are widely scattered and the slope of the regression line was not significantly different from zero (Table 1). Figure 2(b), Figure 2(c) show the SRR for Pacific bluefin tuna plotted for shorter periods. In each period, the SRR showed anticlockwise loops.
![]()
Figure 7. Comparison of stock-recruitment relationship simulated and observed. (a) Result of simulation when Model 4 is used (m = 2). (b) Stock-recruitment relationship observed for the pacific stock of Japanese sardine.
4. Discussion
SRRs for the Pacific stock of Japanese sardine and that for Pacific bluefin tuna seem to be quite different. The former has a positive relationship between ln(R) and ln(S), but the latter seems to have no relationship between ln(R) and ln(S). However, simulations conducted in this paper showed that those apparent SRRs could be reproduced by the same model shown in Equation (1).
For species with a short reproductive cycle, such as sardines, the cycle of environmental conditions will be longer than the reproduction cycle for the species. Therefore, the apparent SRRs for the species will show increasing loops. This can also be seen in the SRRs for anchovies [15] , mackerel and other species [16] . On the contrary, for species with a long reproduction cycle, the apparent SRRs will scatter widely and will show anticlockwise loops with no trend, such as that observed in bluefin tuna.
Generally, in species with a long period of maturation, the behavior of the apparent SRRs will be much more complicated, because the maturity age is biologically determined species by species whereas the cycle of environmental conditions can easily change depending on circumstances. When the maturity age is long, the half- cycle of environmental conditions is usually shorter than the maturity age; however, it can easily occur in a certain period that the half-cycle of environmental conditions happens to be longer than the maturity age. Further, the survival process will also be changed in response to the intensity of harvesting. Therefore, in cases when the maturity age is long, the apparent shape of the SRR is much more complicated than when the maturity age is short.
Figure 8 shows the mechanism by which the clockwise or anticlockwise loop emerges. Figure 8 shows the case, as an example, when Equation (1) produces a cyclically fluctuation in R with 20-year cycle. The S also fluctuates cyclically with 2-year 1) or 13-year 2) time lags in relation to R when the age-at-maturity is 2 years 1) or 13 years 2), respectively. In the trajectories of these R and S values, we can separate four periods, P1, P2, P3 and P4, depending on the combination of increasing and decreasing trends of R and S.
In each period, the blue and red arrows indicate the vector of R and S, the lengths of which are determined by the number of years in the period. For the upper panel, 1) in period P1, both R and S increase; then the direction of the combined vector takes the northeastward direction. P1 is composed of 9 years; then the length of vectors is described by long arrows. 2) In period P2, R decreases but S increases; then the direction of the combined vector takes the southeastward direction. P2 is composed of only 3 years, and the length of vectors is described by short arrows. 3) In period P3, both R and S decrease; then the direction of the combined vector takes the southwestward direction. 4) In period P4, R increases but S decreases; then the direction of the combined vector takes the northwestward direction. The periods occur in the order P1, P2, P3 and P4; then, the trajectory of SRR shows a clockwise loop.
The anticlockwise loop occurs when the phase between R and S is greater than the half-length of the cycle (m = 13) as shown in Figure 8(b). In this case, the trajectory of SRR shows an anticlockwise loop. The SRR for the North Sea haddock, Melano grammus aeglefinus, may be listed as another example of this case [16] .
Under the condition that the cycle of the environmental condition was 20 years and the maturity age was 13, the shape of the SRR derived from the simulation coincided well with the SRR for Pacific bluefin tuna, although,
![]()
Figure 8. A clockwise or anticlockwise loop emerges when R and S are cyclically fluctuating. Blue and red sine curves denote R and S of a 20-year cycle. (a) Maturity age (m) is set at 2 years or (b) 13 years. Depending on whether R and S are increasing or decreasing, the trajectories can be separated into four periods shown by P1, P2, P3 and P4. When m = 2, the trajectory of SRR shows a clockwise loop and when m = 13, the trajectory shows an anticlockwise loop.
in the simulations, if the length of the environmental cycle is longer than 20 years, the maturity age will also be longer than 13 years. Therefore, it is generally considered that the maturity age of Pacific bluefin tuna is 5 years and older; however, the average maturity age must be much greater than 5-years. If the average maturity age is more than 10 years, another interpretation for Figure 4(a) can be done. That is, high R values during 1960-1964 caused the high S values during 1977-1981 and the increasing pattern in R during 1965-1978 caused a pattern of increase in S during 1985-1996, and the decreasing pattern in R during 1978-1993 caused the decreasing pattern in S during 1997-2010. If this interpretation is correct, we can expect that the S in the next decade will increase again in response to the high R values from 1998 to 2008. However, this may be too optimistic a forecast. If overfishing for juvenile fish occurred during those years, the increase in S in the next decade will not materialize. For better accuracy, a much more detailed simulation must be conducted, as Sakuramoto did for the Pacific stock of Japanese sardine [9] .
In the simulations conducted in this paper, the S is assumed to be composed of only one age-class (m-year-old fish). However, both the S of sardine and bluefin tuna are composed of several age classes. Therefore, simulations assuming iteroparous species should also be conducted, although the essential results will not be largely different.
In this study, the effects of process and/or observed errors that surely exist in both R and S are not discussed. Generally, these errors would have the effect of hiding the real relationship between R and S [17] . Therefore, those factors must appear to have no relationship between R and S.
It should be emphasized that the essential mechanism in SRR is very simple. R and S are inseparable. That is, R in the t-th generation produces S in the (t + m)-th generation, and the S in the (t + m)-th generation produces the R in the (t + m + 1)-th generation as shown in Figure 1. Because both processes, from R to S and from S to R, are essentially proportional, the R in the t-th generation is the S in the (t + m)-th generation, and the S in the (t + m)-th generation is the R in the (t + m + 1)-th generation, although the values themselves are different. In other words, the essential mechanism in SRR is only the relationship between Rt and Rt+m+1, or St−1 and St+m as shown in Figure 1. Therefore, if the Rt (or St) fluctuates cyclically in response to environmental factors, the mechanism in SRR is only the relationship between the two points, Rt and Rt+m+1 or St-1 and St+m on the same curve.
5. Conclusions
Stock-recruitment relationships for the Pacific stock of Japanese sardine and that for Pacific bluefin tuna can be expressed by the same model shown in Equation (1). That is, ![]() , where Rt and St−1 denote the recruitment in year t and spawning stock biomass in year t − 1, and f(.) denotes a function that evaluates the effects of environmental factors in year t. The variable
, where Rt and St−1 denote the recruitment in year t and spawning stock biomass in year t − 1, and f(.) denotes a function that evaluates the effects of environmental factors in year t. The variable ![]() is a vector representing the environmental factors.
is a vector representing the environmental factors.
The cyclic environmental conditions strongly affect the stock-recruitment relationships. For species with a short reproductive cycle, such as sardines, the cycle of environmental conditions will be longer than the reproduction cycle for the species. In this case, the apparent SRRs for the species will show increasing loops. On the contrary, for species with a long reproduction cycle, the apparent SRRs will scatter widely and will show anticlockwise loops with no trend, such as that observed in bluefin tuna.
Acknowledgements
I thank Drs. Masanori Miyahara, Tokio Wada, Tatsu Kishida, Jiro Suzuki, Rikio Sato, Seizo Hasegawa, Yukimasa Ishida, Mitsuo Sakai and Naoki Suzuki for their useful comments that improved this manuscript.