Received 16 November 2015; accepted 7 December 2015; published 10 December 2015


1. Introduction
Not only the familiar probability theory, which is established by Kolmogrov relying on the measure theory, but also Ramsey’s [1] theory depends on the frequency theory of probability. The measure theoretic approach is ultimately meaningless without the law of large numbers (i.e. ergodic property) because the exact shapes of the density function and/or cumulative distribution function are unknowable.
Ramsey discards the law of large numbers because everyday samples are usually small in size. Instead, he constructs his theory by relying only on the subjective mathematical expectation, which, of course, does not relate to the law of large numbers at all. The subjective probability, p, is defined the ratio of the subjectively expected number of occurrences, m, from the total number of incidences, n. That is,
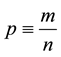 . (1)
. (1)
The most prominent feature of his theory is that he connects the subjective probability with one’s action towards the proposition in question. He assumes that one can know whether the proposition is right if one pays some investigation cost, 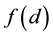 , where d denotes the difficulty of knowing the true causality. In addition, he also assumes that whenever one acts in accordance with the belief that the proposition in question is true, his expected subjective gain from such behavior must be equal to the gain obtained by knowing the truth. Unless such a relationship upholds, he surely ceases to act charted by the belief (i.e. subjective probability), and instead, ascertains the true causality at the cost
, where d denotes the difficulty of knowing the true causality. In addition, he also assumes that whenever one acts in accordance with the belief that the proposition in question is true, his expected subjective gain from such behavior must be equal to the gain obtained by knowing the truth. Unless such a relationship upholds, he surely ceases to act charted by the belief (i.e. subjective probability), and instead, ascertains the true causality at the cost 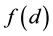 when having decided on the action. It is natural to assume that f is an increase function of d.
when having decided on the action. It is natural to assume that f is an increase function of d.
Let the benefit obtained when the proposition is true be denoted as a and as b when it is false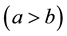 . The subjectively expected gain from the n times trials,
. The subjectively expected gain from the n times trials, 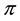 , is
, is
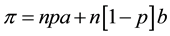 . (2)
. (2)
If one, otherwise, accesses the true causality in each trial, gain, 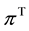 , becomes
, becomes
 . (3)
. (3)
It is assumed that Equation (2) is equalized to (3); then, taking Equation (1) into consideration, we obtain the subjective probability (i.e. the belief on the validity of the proposition), p, as
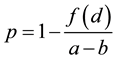 . (4)
. (4)
Equation (4) implies a serious meaning. Along with an increase in the difficulty of understanding and checking the proposition in question, individuals become less confident to it. The reason is that the more complex the proposition becomes, the more costs are incurred for examining its truthfulness. Such kind of tendency is quite prevalent in everyday life.
In relation to economic theory, there is acute difference on the difficultness necessary for understanding between Keynesian theory and monetarism. As Otaki ([3] and [4] ) shows, Keynesian theory upholds when people merely believe that the value of money, which is defined by the inverse of the price index, is not affected by a change in nominal money supply. In other words, as long as people rationally believe the intrinsic value of money, money becomes non-neutral.
In contrast to such a simple structure of Keynesian economics, as Otaki [4] shows, monetarism requires much information and complex processing to understand and believe it; every individual is incessantly concerned about the movement of nominal money supply and all must investigate whether the price level increases proportionately to nominal money supply; and they all must exactly know the value of Marshallian k. To summarize, the value, d, of monetarism can be deemed to be much larger than that of the Keynesian thesis.
This implies that, ceteris paribus, Keynesian economics becomes more confident among laypeople than monetarism. As such, if people behave in accordance with their confidence in a theory, the economy in reality becomes to possess the properties of Keynesian economics.
The rest of this paper is organized as follows. Section 2 constructs a model based on Otaki [2] [3] , and [4] with Ramsey’s [1] concept of belief and shows the plausibility of Keynesian economics being superior to monetarism. Section 3 is the brief concluding remarks.
2. Plausibility of Keynesian Economics
2.1. Two Alternative Models
A two-period overlapping-generations model with infinite time horizon is considered, as in Otaki [2] and [4] . There is no population growth and every individual has an identical utility function:
 , (5)
, (5)
where  is the consumption level of good
is the consumption level of good 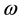 of an individual, who is born at the beginning of period t, during his i-th stage of life.
of an individual, who is born at the beginning of period t, during his i-th stage of life. 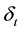 is a definition function the value of which takes unity when the individual is employed and zero when unemployed.
is a definition function the value of which takes unity when the individual is employed and zero when unemployed.  is the disutility of labor supply.
is the disutility of labor supply.
For simplicity, it is assumed that the marginal productivity of labor is unity and that there is no fixed cost. All firms are price takers, and thus, earned profits become zero in equilibrium. In addition, this model assumes that the labor market is in interior equilibrium where some individuals are always unemployed, and the equilibrium nominal wage stacks at the nominal reservation wage. These assumptions yield the following equation:
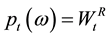 , (6)
, (6)
where ![]() is the price of good
is the price of good ![]() and
and ![]() is the nominal reservation wage during period t. From the property of the indirect utility function, which corresponds to Equation (5), the nominal reservation wage becomes
is the nominal reservation wage during period t. From the property of the indirect utility function, which corresponds to Equation (5), the nominal reservation wage becomes
![]() (7)
(7)
Combining Equations (6) and (7), the equilibrium inflation rate, ![]() , is determined as
, is determined as![]() . Furthermore, an elementary calculus gives us the following aggregate consumption function of the young generation,
. Furthermore, an elementary calculus gives us the following aggregate consumption function of the young generation,![]() :
:
![]() , (8)
, (8)
where ![]() is the real GDP in terms of the current goods. Consequently, one obtains the goods market equilibrium condition as
is the real GDP in terms of the current goods. Consequently, one obtains the goods market equilibrium condition as
![]() , (9)
, (9)
where ![]() is the nominal money supply at the beginning of period t. The second term of the right-hand side of
is the nominal money supply at the beginning of period t. The second term of the right-hand side of
Equation (9) is the real total expenditure of the old generation, ![]() , and the government expenditure financed by printing money,
, and the government expenditure financed by printing money,![]() . It is assumed that the economy is located at the stationary state after period t,
. It is assumed that the economy is located at the stationary state after period t,
and hence the monetary authority keeps the real money supply constant. That is, the growth rate of money is fixed at![]() .
.
Equation (9) contains two undetermined endogenous variables; real GDP![]() ; the initial price level
; the initial price level![]() . Hence one more structural equation is necessary to close the model. This means that the structure of an economy essentially depends on how individuals evaluate the value of money. If they believe that the intrinsic value of money is independent of nominal money supply, the initial price level remains intact even after a change in the nominal money supply under rational expectations equilibrium, and money becomes non-neutral. That is, the additional equation to close the model in accordance with the Keynesian proposition is
. Hence one more structural equation is necessary to close the model. This means that the structure of an economy essentially depends on how individuals evaluate the value of money. If they believe that the intrinsic value of money is independent of nominal money supply, the initial price level remains intact even after a change in the nominal money supply under rational expectations equilibrium, and money becomes non-neutral. That is, the additional equation to close the model in accordance with the Keynesian proposition is
![]() (const.) (10)
(const.) (10)
On the other hand, when people believe that the value of money is not absolute but relative, the monetarist assertion to close the model is summarized by the following equilibrium price function:
![]() . (11)
. (11)
One must note both resulting equilibria are self-fulfilling. From Equations (10) and (11), it is clear that the equilibrium GDP earned under Keynesian proposition, ![]() , is larger than that earned under monetarism,
, is larger than that earned under monetarism, ![]() , as long as the initial price level,
, as long as the initial price level, ![]() , is sufficiently low and the value of money is high enough. Henceforth, let be assumed that
, is sufficiently low and the value of money is high enough. Henceforth, let be assumed that![]() . In addition, the corresponding Marshallian ks are denoted as
. In addition, the corresponding Marshallian ks are denoted as![]() , respectively (
, respectively (![]() )1.
)1.
2.2. Ramsey’s Belief and Keynesian Economics
This subsection applies the Ramsey’s formula (4) to examine which of the two above mentioned macroeconomic theses is plausible. Before undertaking the analysis, one must clarify what kind of knowledge is needed for a layperson in economics to understand each theory.
1) For the Keynesian theory, the layperson must be able to confirm that the current price level, ![]() , is unchanged despite a change in the nominal money supply as in Equation (10).
, is unchanged despite a change in the nominal money supply as in Equation (10).
2) For monetarism a) the layperson must be able to confirm that the current price level changes proportionately with the nominal supply as in Equation (11), b) he must be conversant with the linear function to understand the relationship in a), and c) he must know the value of the proportional constant ![]() (Marshallian k) and the exact quantity of nominal money supply,
(Marshallian k) and the exact quantity of nominal money supply,![]() .
.
As such, it is evident that the monetarist thesis is far more difficult and laborious to understand than the Keynesian theory. Accordingly the value of d in Equation (4) is thought to be much larger in the case of monetarism.
In addition, whenever the true proposition is the Keynesian thesis, it is assumed that the subjective distribution when the proposition is false is uniform within the interval![]() . Thus, the difference in gains between the action based on the correct proposition and that based on the wrong one, which corresponds to
. Thus, the difference in gains between the action based on the correct proposition and that based on the wrong one, which corresponds to ![]()
in Equation (4), is![]() . Similarly, whenever the true proposition is monetarism, the probability distribu-
. Similarly, whenever the true proposition is monetarism, the probability distribu-
tion of such proposition being false is uniform within![]() . Accordingly, such a difference also becomes
. Accordingly, such a difference also becomes
![]() . (12)
. (12)
Hence, the denominators in Equation (4) are the same value independent of whether the true proposition is Keynesian or monetarism2. This implies, therefore, that the belief in Keynesian thesis, ![]() , is much higher than that in monetarism,
, is much higher than that in monetarism,![]() . If people behave in accordance with proposition more confident about, such behavior becomes self-enforcing, and the economy moves as predicted by Keynesian economics. This study defines this property as the plausibility of Keynesian economics3.
. If people behave in accordance with proposition more confident about, such behavior becomes self-enforcing, and the economy moves as predicted by Keynesian economics. This study defines this property as the plausibility of Keynesian economics3.
3. Concluding Remarks
This study develops the concept of plausibility in alternative monetary theories with the key concept being Ramsey’s [1] belief. While Keynesian economics is upheld only by the belief in the stable value of money in terms of goods, monetarism is not sustained until laypeople in economics understand not only the exact linear relationship between the nominal money supply and the price index but also macroeconomic statistics with which they are almost unconcerned in everyday life. Consequently, the cost for knowing the truth is much cheaper in the Keynesian thesis. This implies that Keynesian economics is more plausible than monetarism although both theories possess the self-fulfilling property. In this sense, Ramsey’s theory can be regarded as an effective equilibrium selection procedure.
Acknowledgements
The author is grateful for the incisive comments of reviewers, and he also appreciates Professor Susumu Cato and Doctor Masaoki Tamura for encouraging discussion. The basic research of this paper is funded by MEXT/ JSPS KAKENHI Grant Number 60183761.
NOTES
![]()
1Note that knowing the resulting benefits empirically does not necessarily mean that all individuals are informed of the whole structure of the economy.
![]()
2Note that there is no economic surplus in this simplified setting. However, as Otaki [2] and [4] shows, if the equilibrium concept of goods markets is interchanged with monopolistic competition instead of perfect competition, there emerges an economic surplus that is proportional to the real GDP.
3Ramsey [1] proves the existence of more general type of belief based on an axiomatic approach, which includes the availed belief in this paper as a special case. In this sense, there is a certain limit in this paper. Ramsey [1] begins with defining the proposition the probability of which is 1/2. Subsequently, by using the assumption of some kind of rationality, he succeeds in achieving to allot the degree of belief to all general propositions. About the rationality, he denotes
“I propose to take as a basis a general psychological theory, which is now universally discarded, but nevertheless comes. I think fairly close to the truth in the sort of cases with which we are most concerned. I mean the theory that we act in the way so that a person’s actions are completely determined by his desire and opinions.” (p. 69)
This is quite akin to the concept of the economic rationality despite his aversion to utilitarianism. In addition, it is necessary for more fruitful analysis on the concept of plausibility to explore how human cognition progresses. In my model, this problem closely connects with how we should determine the value of d, although I still remain in assuming that d is an increasing function of the number of knowledge.
Keynes [5] prophets
“Thus he [Ramsey] was led to consider `human logic’ as distinguished from ‘formal logic’. Formal logic is concerned with nothing but the rules of consistent thought. But in addition to this we have certain ‘useful mental habits’ for handling the material with which we are supplied by our perceptions and by our memory and perhaps in other way, and so arriving at or towards truth; and the analysis of such habit is also a sort of logic. The application of these ideas to the logic of probability is very fruitful.” (p. 338)