Received 27 April 2014; accepted 4 December 2015; published 7 December 2015

1. Introduction
In this paper, we find a formula depending on determinants for the solutions of the following linear equation
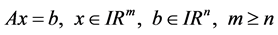 (1)
(1)
or
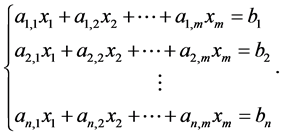 (2)
(2)
Now, if we define the column vectors
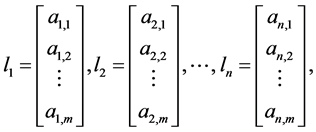
then the system (2) also can be written as follows:
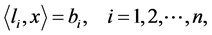 (3)
(3)
where ![]() denotes the innerproduct in
denotes the innerproduct in ![]() and A is
and A is ![]() real matrix. Usually, one can apply Gauss Elimination Method to find some solutions of this system, and this method is a systematic procedure for solving systems like (1); it is based on the idea of reducing the augmented matrix
real matrix. Usually, one can apply Gauss Elimination Method to find some solutions of this system, and this method is a systematic procedure for solving systems like (1); it is based on the idea of reducing the augmented matrix
![]() (4)
(4)
to the form that is simple enough such that the system of equations can be solved by inspection. But, to my knowledge, in general there is not formula for the solutions of (1) in terms of determinants if![]() .
.
When ![]() and
and![]() , the system (1) admits only one solution given by
, the system (1) admits only one solution given by![]() , and from here one can deduce the well known Cramer Rule which says:
, and from here one can deduce the well known Cramer Rule which says:
Theorem 1.1. (Cramer Rule 1704-1752) If A is ![]() matrix with
matrix with![]() , then the solution of the system (1) is given by the formula:
, then the solution of the system (1) is given by the formula:
![]() (5)
(5)
where ![]() is the matrix obtained by replacing the entries in the ith column of A by the entries in the matrix
is the matrix obtained by replacing the entries in the ith column of A by the entries in the matrix
![]()
A simple and interested generalization of Cramer Rule is done by Prof. Dr. Sylvan Burgstahler ( [1] ) from University of Minnesota, Duluth, where he taught for 20 years. This result is given by the following Theorem:
Theorem 1.2. (Burgstahler 1983) If the system of equations
![]() (6)
(6)
has(unique) solution![]() , then for all
, then for all ![]() one has
one has
![]() . (7)
. (7)
Using Moore-Penrose Inverse Formula and Cramer’s Rule, one can prove the following Theorem. But, for better understanding of the reader, we will include here a direct proof of it.
Theorem 1.3. For all![]() , the system (1) is solvable if, and only if,
, the system (1) is solvable if, and only if,
![]() (8)
(8)
Moreover, one solution for this equation is given by the following formula:
![]() (9)
(9)
where ![]() is the transpose of A (or the conjugate transpose of A in the complex case).
is the transpose of A (or the conjugate transpose of A in the complex case).
Also, this solution coincides with the Cramer formula when![]() . In fact, this formula is given as follows:
. In fact, this formula is given as follows:
![]() (10)
(10)
where ![]() is the matrix obtained by replacing the entries in the jth column of
is the matrix obtained by replacing the entries in the jth column of ![]() by the entries in the matrix
by the entries in the matrix
![]()
In addition, this solution has minimum norm, i.e.,
![]() (11)
(11)
and![]() .
.
The main results of this work are the following Theorems.
Theorem 1.4. The solutions of (1)-(3) given by (9) can be written as follows:
![]() (12)
(12)
Theorem 1.5. The system (1) is solvable for each![]() , if, and only if, the set of vectors
, if, and only if, the set of vectors ![]() formed by the rows of the matrix A is lineally independent in
formed by the rows of the matrix A is lineally independent in![]() .
.
Moreover, a solution for the system (1) is given by the following formula:
![]() (13)
(13)
![]() (14)
(14)
where the set of vectors ![]() is obtain by the Gram-Schmidt process and the numbers
is obtain by the Gram-Schmidt process and the numbers ![]() are given by
are given by
![]() (15)
(15)
and![]() .
.
2. Proof of the Main Theorems
In this section we shall prove Theorems 1.3, 1.4, 1.5 and more. To this end, we shall denote by ![]() the Euclidian innerproduct in
the Euclidian innerproduct in ![]() and the associated norm by
and the associated norm by![]() . Also, we shall use some ideas from [2] and the following result from [3] , pp 55.
. Also, we shall use some ideas from [2] and the following result from [3] , pp 55.
Lemma 2.1. Let W and Z be Hilbert space, ![]() and
and ![]() the adjoint operator, then the following statements holds,
the adjoint operator, then the following statements holds,
[(i)] ![]() such that
such that
![]()
[(ii)]![]() .
.
We will include here a direct proof of Theorem 1.3 just for better understanding of the reader.
Proof of Theorem 1.3. The matrix A may also viewed as a linear operator![]() ; therefore
; therefore ![]() and its adjoint operator
and its adjoint operator ![]() is the transpose of A and
is the transpose of A and![]() .
.
Then, system (1) is solvable for all ![]() if, and only if, the operator A is surjective. Hence, from the Lemma 2.1 there exists
if, and only if, the operator A is surjective. Hence, from the Lemma 2.1 there exists ![]() such that
such that
![]()
Therefore,
![]()
This implies that ![]() is one to one. Since
is one to one. Since ![]() is a
is a ![]() matrix, then
matrix, then![]() .
.
Suppose now that![]() . Then
. Then ![]() exists and given
exists and given ![]() we can see that
we can see that ![]() is a solution of
is a solution of![]() .
.
Now, since ![]() is the only solution of the equation
is the only solution of the equation
![]()
then from Theorem 1.1 (Cramer Rule) we obtain that:
![]()
where ![]() is the matrix obtained by replacing the entries in the ith column of
is the matrix obtained by replacing the entries in the ith column of ![]() by the entries in the matrix
by the entries in the matrix
![]()
Then, the solution ![]() of (1) can be written as follows
of (1) can be written as follows
![]()
Now, we shall see that this solution has minimum norm. In fact, consider w in ![]() such that
such that ![]() and
and
![]()
On the other hand,
![]()
Hence,![]() .
.
Therefore, ![]() , and
, and ![]() if
if![]() .
.
Proof of Theorem 1.5. Suppose the system is solvable for all![]() . Now, assume the existence of real numbers
. Now, assume the existence of real numbers ![]() such that
such that
![]()
Then, there exists ![]() such that
such that
![]() .
.
In other words,
![]()
Hence,
![]()
So,
![]()
Therefore, ![]() , which prove the independence of
, which prove the independence of![]() .
.
Now, suppose that the set ![]() is linearly independent in
is linearly independent in![]() . Using the Gram-Schmidt process we can find a set
. Using the Gram-Schmidt process we can find a set ![]() of orthogonal vectors in
of orthogonal vectors in ![]() given by the formula:
given by the formula:
![]() . (16)
. (16)
Then, system (1) will be equivalent to the following system:
![]() , (17)
, (17)
where
![]() . (18)
. (18)
If we denote the vectors![]() ’s by
’s by
![]()
and the ![]() matrix
matrix ![]() by
by
![]()
then, applying Theorem 1.3 we obtain that system (17) has solution for all ![]() if, and only if,
if, and only if, ![]() . But,
. But,
![]() .
.
So,
![]()
From here and using the formula (9) we complete the proof of this Theorem.
Examples and Particular Cases
In this section we shall consider some particular cases and examples to illustrate the results of this work.
Example 2.1. Consider the following particular case of system (1)
![]() (19)
(19)
In this case ![]() and
and![]() . Then, if we define the column vector
. Then, if we define the column vector
![]()
![]()
Then, ![]() and
and
![]()
Therefore, a solution of the system (19) is given by:
![]() (20)
(20)
Example 2.2. Consider the following particular case of system (1)
![]() (21)
(21)
In this case ![]() and
and
![]()
Then, if we define the column vectors
![]()
then
![]()
Hence, from the formula (10) we obtain that:
![]() .
.
Therefore, a solution of the system (21) is given by:
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() . (25)
. (25)
Now, we shall apply the foregoing formula or (12) to find the solution of the following system
![]() . (26)
. (26)
If we define the column vectors
![]()
then ![]() and
and![]() ,
, ![]() , and
, and![]() .
.
Example 2.3. Consider the following general case of system (1)
![]() . (27)
. (27)
Then, if ![]() is an orthogonal set in
is an orthogonal set in![]() , we get
, we get
![]()
and the solution of the system (1) is very simple and given by:
![]() (28)
(28)
Now, we shall apply the formula (28) or (12) to find solution of the following system:
![]() . (29)
. (29)
If we define the column vectors
![]()
Then, ![]() is an orthogonal set in
is an orthogonal set in ![]() and the solution of this system is given by:
and the solution of this system is given by:![]() ,
, ![]() ,
, ![]() and
and![]() .
.
3. Variational Method to Obtain Solutions
Theorems 1.3, 1.4 and 1.5 give a formula for one solution of the system (1) which has minimum norma. But it is not the only way allowing to build solutions of this equation. Next, we shall present a variational method to obtain solutions of (1) as a minimum of the quadratic functional![]() ,
,
![]() (30)
(30)
Proposition 3.1. For a given ![]() the Equation (1) has a solution
the Equation (1) has a solution ![]() if, and only if,
if, and only if,
![]() (31)
(31)
It is easy to see that (31) is in fact an optimality condition for the critical points of the quadratic functional j define above.
Lemma 3.1. Suppose the quadratic functional j has a minimizer![]() . Then,
. Then,
![]() (32)
(32)
is a solution of (1).
Proof. First, we observe that j has the following form:
![]()
Then, if ![]() is a point where j achieves its minimum value, we obtain that:
is a point where j achieves its minimum value, we obtain that:
![]()
So, ![]() and
and ![]() is a solution of (1).
is a solution of (1).
Remark 3.1. Under the condition of Theorem 1.3, the solution given by the formulas (32) and (9) coincide.
Theorem 3.1. The system (1) is solvable if, and only if, the quadratic functional j defined by (30) has a minimum for all![]() .
.
Proof. Suppose (8) is solvable. Then, the matrix A viewed as an operator from ![]() to
to ![]() is surjective. Hence, from Lemma 2.1. there exists
is surjective. Hence, from Lemma 2.1. there exists ![]() such that
such that
![]()
Then,
![]()
Therefore,
![]()
Consequently, j is coercive and the existence of a minimum is ensured.
The other way of the proof follows as in proposition 3.1.
Now, we shall consider an example where Theorems 1.3, 1.4 and 1.5 can not be applied, but proposition 3.1 does.
Example 3.1. It considers the system with linearly independent rows
![]() .
.
In this case ![]() and
and
![]()
Then
![]()
Therefore, the critical points of the quadratic functional j given by (30) satisfy the equation:
![]()
i.e.,
![]() .
.
So, there are infinitely many critical points given by
![]()
Hence, a solution of the system is given by
![]() .
.