Received 10 October 2015; accepted 27 November 2015; published 30 November 2015


1. Introduction
Environmental pollution and the consequent climate change have induced many game theorists to study these topics through mathematical games. When players (countries, regions, etc.) cooperate, each player pollutes less than under a non cooperative behavior and the more the cooperating countries, the greater the total benefit. An example is the pollution of shallow lakes, an interesting question studied in [1] . If all decision-makers cooperated, shallow lakes could remain clean, but in fact only a part of players cooperate so they (and we) do not reach the optimum.
In our models, we consider n players where some work together, so we speak of partial cooperative games. These models arise from the observation of real life.
This is the ancient problem named “The tragedy of Commons” [2] , and deeply studied by many authors, such as in [3] and [4] . The overexploitation of commons, the selfish pursuit of one’s own benefit can lead to the worst social outcome.
Is it possible for individuals to cooperate without being compelled by a law? (see [3] ). Since there are no institutions which can enforce international environmental agreements (IEAs), international cooperation is very difficult.
In order to contain the emissions of pollutants, in 1997 the Kyoto Protocol to the “Framework Convention on Climate Change” limited emissions of carbon dioxide, methane, nitrous oxide, halocarbons, perfluorocarbons and sulfur hexafluoride, but the pollution problem is far from being solved satisfactorily.
Many environmental problems are studied in [5] -[9] .
An interesting approach was made in [10] , where the author makes a model through a cooperative game with non-empty core.
Over the past few years, many game theorists were interested in the problem of coalition formation (see [11] - [16] and references in these).
It seems to us that the mathematical game theory offers a natural medium to the study of environmental models. Our approach to such a problem is to study a cooperative situation modeled by a coalitional game 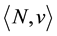 and to define, based on it, a new game which shows the process of making coalitions in the initial model.
and to define, based on it, a new game which shows the process of making coalitions in the initial model.
In the applications to real life, it is natural to consider multicriteria situations, because a player wishes to “optimize” multiple criteria. For example, one problem is to reduce pollution and to increase production, two objectives which are often opposed or not compatible. In the classic approach to TU-games, an allocation rule is defined to predict how rational players distribute among them the gain from cooperation. In our model, we study a game where players have multiple criteria “to optimize” and propose a new concept of solution (coalitional Pareto equilibrium), using an allocation rule to define the players’ payoff.
About multicriteria or vector games, see [16] -[20] .
In the text, we will use equally the words “multicriteria” or “multiobjective” or “vector” games. We will use “multicriteria partial cooperative games” or “multiobjective environmental games” when only a proper subset of N is formed by cooperating players.
This paper is organized as follows: in Section 2, we set up notations and known results which will be useful for our model, in Section 3, we describe a non-cooperative model called participation game inspired by Monderer and Shapley’s model [13] , and then we provide a new solution for a partial cooperative game (or environmental game) and an existence result. Section 4 contains conclusions and some ideas for further research. Many examples illustrate the paper.
2. Notations and Preliminary Results
In this section we consider multiobjective problems that are models where the decision makers have many objectives “to optimize”.
Let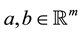 ,
, 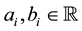 , we consider the following preferences:
, we consider the following preferences:
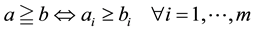 ;
;
 and
and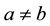 ;
;
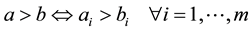 .
.
Analogously we define ,
,  ,
,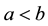 .
.
Let us consider a multiobjective (or multicriteria) TU-game 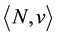 where N is the set of n players and
where N is the set of n players and 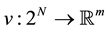 is the characteristic function of the game, with
is the characteristic function of the game, with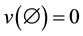 . It assigns to each coalition
. It assigns to each coalition 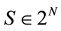 a m-vector, m being the number of objectives, equal for each player:
a m-vector, m being the number of objectives, equal for each player:
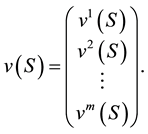
In an environmental game, if all players cooperate, the grand coalition forms and obtains the best (we will specify the meaning in the next pages).
Let us write
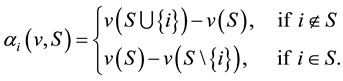
Definition 2.1 A multicriteria game ![]() is convex if
is convex if
![]()
![]() and
and![]() .
.
Definition 2.2 We call i a dummy player if![]() ,
,![]() .
.
Now let us define one solution for a cooperative game: the Shapley value. It was introduced by Shapley in the fifties. It is one of the most interesting solution concepts in the cooperative game theory. Intuitively it has a link with the average of the marginal contributions of each player joing (see [14] [19] for more details).
Definition 2.3 The Shapley value of ![]() denoted by
denoted by![]() , is defined, for each player
, is defined, for each player ![]() by
by
![]()
where s and n denote the cardinality of the coalitions S and N respectively.
Keep in mind that an allocation rule ![]() is a map which assigns to each multicriteria TU-game
is a map which assigns to each multicriteria TU-game ![]() an element of
an element of![]() .
.
A “good” allocation rule verifies the following axioms:
1) Efficiency property (EFF for short):![]() .
.
2) Weak Monotonicity property (WMON for short): given two games![]() ,
, ![]() such that
such that ![]()
![]() and
and ![]() then
then![]() .
.
3) Dummy Out property (DUMOUT for short): for all ![]() and all set of dummies
and all set of dummies![]() , it turns out
, it turns out ![]() for all
for all ![]() where
where ![]() is the restriction of the characteristic function v to the set
is the restriction of the characteristic function v to the set ![]() of players. Intuitively, if the dummies of a game abandon it, others are unaffected and the allocation does not change.
of players. Intuitively, if the dummies of a game abandon it, others are unaffected and the allocation does not change.
The Shapley value verifies the three axioms written.
To explain better the notations, let us consider the following:
Example 2.1 Let ![]() be a cooperative game with two criteria:
be a cooperative game with two criteria:
where we mean![]() ,
, ![]() , ...
, ...![]() , ... and so on.
, ... and so on.
The first objective is the reduction of pollution percentage and the second is the increase of industrial production. If player (industry) 1 decides to act alone, its production increases by 15% but it can reduce its pollution only by 10%. If player 1 cooperates with player 2 (a second industry), their production increases by 50% and they can reduce their pollution combined by 40%... If all players cooperate, they increase their production by 80% and reduce their pollution of 90%. The Shapley value for this bi-criteria game is:
![]()
Let us consider a multicriteria non cooperative game ![]() where
where ![]() is the set of players,
is the set of players, ![]() is the set of strategies of player i and ui is the payoff function of player i,
is the set of strategies of player i and ui is the payoff function of player i,
![]()
For![]() , we write
, we write ![]() and
and ![]() denotes the restriction of an
denotes the restriction of an ![]() to
to![]() .
.
To define environmental games and a solution for them, we need one for cooperative games (for example the aforementioned Shapley value) as well as one for non cooperative games. To this end, we remember the definition of Pareto equilibrium (PE for short), which is the commonly used solution for (non-cooperative) multiobjective games.
Definition 2.4 Let G be a multicriteria non-cooperative game.
A strategy profile ![]() is a
is a
1) weak Pareto equilibrium if ![]()
![]() ;
;
2) strong Pareto equilibrium if ![]()
![]() .
.
The set of weak and strong Pareto equilibria will be denoted by wPE and sPE respectively.
Intuitively ![]() is a weak (strong) Pareto equilibrium for the game G if there isn’t a
is a weak (strong) Pareto equilibrium for the game G if there isn’t a ![]() strategy increasing the payoff for player i.
strategy increasing the payoff for player i.
Example 2.2 Let G be the bicriteria non cooperative game in the table below
Two countries (players) have two strategies: to reduce their sulphur dioxide emissions (C) or not to reduce (nC).
They have two objectives to pursue: to save the cost of the national health institute and to increase the people health.
In pure strategies the equilibria are:
![]() .
.
In this paper we are not interested in mixed strategies.
3. From a Coalition Game to a Strategic One
There are no doubts that we must reduce the pollution following carbon dioxide emissions. One of the most serious problems is the contribution of each country. In this paper we suggest such models and a solution (the coalitional Pareto equilibrium) as will enable all countries to obtain the best through cooperation.
In many practical situations, the interaction among decision-makers may be a mix of cooperative and non- cooperative behavior.
Although the players in the same coalition cooperate, there are also coalitions made up of only one player. Furthermore different coalitions do not cooperate with each other.
In such models we speak of partial cooperative games or environmental games (about partial cooperation, see [6] [21] [22] ).
Let us consider ![]() a multicriteria cooperative TU-game and an allocation rule
a multicriteria cooperative TU-game and an allocation rule ![]() which is agreed upon by all players.
which is agreed upon by all players.
By ![]() we mean the restriction of the TU-game
we mean the restriction of the TU-game ![]() to the coalition S. By
to the coalition S. By ![]() we mean the restriction of the allocation rule of the game
we mean the restriction of the allocation rule of the game ![]() to the game
to the game![]() .
.
We can define the non cooperative participation game in normal form ![]() in the following way:
in the following way: ![]() that is the strategies are the coalitions to which the player i would like to belong.
that is the strategies are the coalitions to which the player i would like to belong.
The utility function for player i is defined as follows:
![]()
where ![]()
Intuitively, we start with a TU-game and an allocation rule ![]() agreed upon by all players (for example the Shapley value). Then we trasform it into a strategic game, the participation game, where the players’ strategies are the coalitions to which they wish to belong. The game is static, so the decision-makers propose the coalitions simultaneously and independently of each other. A coalition is created if all its members have proposed it. The utility function gives each player the value of the allocation rule if the coalition forms and the value
agreed upon by all players (for example the Shapley value). Then we trasform it into a strategic game, the participation game, where the players’ strategies are the coalitions to which they wish to belong. The game is static, so the decision-makers propose the coalitions simultaneously and independently of each other. A coalition is created if all its members have proposed it. The utility function gives each player the value of the allocation rule if the coalition forms and the value ![]() of the coalition represented by the single player in any other case. We call this game a multicriteria partial cooperative game or multiobjective environmental games.
of the coalition represented by the single player in any other case. We call this game a multicriteria partial cooperative game or multiobjective environmental games.
In the following definition we generalize the concept of strong Nash equilibrium (sNE for short) to a notion of equilibrium profile for vector games. We call it coalitional Pareto equilibrium.
Definition 3.1 We say that ![]() is a coalitional Pareto equilibrium (for short cP E) of the strategic game
is a coalitional Pareto equilibrium (for short cP E) of the strategic game ![]() if
if ![]() and
and ![]() such that
such that ![]() for some
for some![]() .
.
We note that if ![]() is a cPE with an allocation rule, it could not be a cPE with another allocation rule. If the players have only one objective to pursue, the cPE is a sNE. (About the notion of strong Nash see [12] [23] ).
is a cPE with an allocation rule, it could not be a cPE with another allocation rule. If the players have only one objective to pursue, the cPE is a sNE. (About the notion of strong Nash see [12] [23] ).
Definition 3.2 We say that a multicriteria partial cooperative game has a partial equilibrium if there is a cPE for the corresponding participation game.
Example 3.1 Let us consider the following bicriteria game.
There are three industries (players) which work near a great shallow lake. They have pursue two objectives: the first is the reduction of toxic substances spilt into the lake, the second is the gain of having a lake with clean water, many fishes and green plants. The total cooperation give a real benefit to all.
In this table we write for example:
![]() , which means that the coalition
, which means that the coalition ![]() gains 2 by the reduction of pollution and 3 is the gain to have clean lake. We note that the number represents a total gain (benefit, health, etc.) not necessary money.
gains 2 by the reduction of pollution and 3 is the gain to have clean lake. We note that the number represents a total gain (benefit, health, etc.) not necessary money.
Let the Shapley value be the allocation rule agreed upon by all players. We can use the following table to take a quick look at the coalitional Pareto equilibria (Table 1).
The first two columns represent the game in example 3.1, the others represent the Shapley value relative to the game vS where S is the coalition written in the first column.
There are two cPE:
![]()
and![]() .
.
From Vector Optimization problems we can learn that, the m scalar games generated from breaking down the vector game, do not necessarily inherit its structure.
In fact if we break down the considered bicriteria game of the example 3.1 into two games (the first one pertaining to the first criterion, the second one pertaining the second criterion), we can remark that ![]() is not a sNE for any considered game whereas
is not a sNE for any considered game whereas ![]() is a sNE only for the second one.
is a sNE only for the second one.
We will now provide the following existence theorem for a coalitional Pareto equilibrium.
In the authors’ opinion this is an interesting result, because there is an incentive to cooperate: in the hypotheses of the theorem (which are often verified in the models of real life), if all players cooperate (read: if all countries cooperate), the grand coalition forms and there is an efficient solution for all members.
![]()
Table 1. A bicriteria partial cooperative game.
Theorem 3.1 Let ![]() be a multicriteria convex TU game and φ the Shapley value, then
be a multicriteria convex TU game and φ the Shapley value, then ![]() is a cPE for the multicriteria participation game.
is a cPE for the multicriteria participation game.
Proof. From definition of Shapley value and![]() , it turns out that
, it turns out that![]() .
.
Let us suppose, by contradiction, that ![]() is not a cPE; then
is not a cPE; then![]() ,
, ![]() s.t.
s.t.
![]()
![]() for some.
for some.
This leads us to state that there is at least a component ![]() such that
such that ![]() and
and![]() , even if the coalition
, even if the coalition![]() .
.
This is a contradiction with the properties of![]() .
.
Corollary 3.1 Let G be a multicriteria partial cooperative game. If ![]() is a convex multicriteria TU-game and the allocation rule is the Shapley value, then the game G has at least a partial equilibrium.
is a convex multicriteria TU-game and the allocation rule is the Shapley value, then the game G has at least a partial equilibrium.
Remark 3.1 The result of theorem 3.1 is valid considering an allocation rule verifying the three axioms: EFF, WMON and DUMOUT.
4. Conclusions and Open Problems
Game theorists apply with success the Game Theory to environmental models and emission problems. In this paper, we consider a game where some players cooperate and others do not. We call this game “partial cooperative”. To give a new notion of solution for these games, we start trasforming the structure of a cooperative game into a strategic one. This new game is defined considering as strategies the coalitions to which player i wish to belong and the utility function assigns the Shapley value to each player who wants cooperate and ![]() to player i who does not cooperate.
to player i who does not cooperate.
We provide a new concept of equilibrium for multiobjective environmental games, the coalitional Pareto equilibrium which generalizes the idea of strong Nash. This concept, differently from the Nash equilibrium, captures the idea of efficient equilibrium.
An existence theorem and many examples complete the paper.
As concerns possible further research, it would be interesting to study the partial cooperative problem where the allocation rule is different from the Shapley value or to consider games with utility functions in uncertainty intervals, (see [18] ). Some of these issues are work in progress.
Acknowledgements
The second author has been supported by the Gruppo Nazionale per l’Analisi Matematica, la Probabilitá e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM).
NOTES
![]()
*Corresponding author, the authors’ names are written only in the alphabetic order.