The Mixture of New Integral Transform and Homotopy Perturbation Method for Solving Discontinued Problems Arising in Nanotechnology ()
1. Introduction
Non-linear phenomena that appear in many areas of scientific fields such as solid state physics, plasma physics, fluid mechanics, population models and chemical kinetics, can be modeled by nonlinear partial differential equations. In many different fields of science and engineering, it is important to obtain exact or numerical solution of the nonlinear partial differential equations. Searching of exact and numerical solution of nonlinear equations in science and engineering is still quite problematic that needs new methods for finding the exact and approximate solutions. Most of new nonlinear equations do not have a precise analytic solution; so, numerical methods have largely been used to handle these equations. There are also analytic techniques for nonlinear equations. Some of the classic analytic methods are Lyapunov’s artificial small parameter method [1] , d-expan- sion method [2] , perturbation techniques [3] [4] and Hirota bilinear method [5] [6] . In recent years, many research workers have paid attention to study the solutions of nonlinear partial differential equations by using various numerical methods. Among these are the Adomian decomposition method (ADM) [7] , He’s semi- inverse method [8] , the tanh method, the homotopy perturbation method (HPM), the sinh-cosh method, the differential transform method and the variational iteration method (VIM) [9] [10] .
According to E-infinity theory [11] - [13] , space at the quantum scale is not a continuum, and it is clear that nanotechnology possesses a considerable richness which bridges the gap between the discrete and the continuum [14] - [16] . On nanoscales, He et al. [17] found experimentally an uncertainty phenomenon similar to Heisen- berg’s uncertainty principle in quantum mechanics. Continuum hypothesis on the nanoscales becomes, therefore, invalid. He and Zhu [18] suggested some differential-difference models describing fascinating phenomena arising in heat/electron conduction and flow in carbon nanotubes, among which we will study the following model:
(1)
where 
and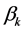 
are constants. Physical interpretation is given in [18] . Equation (1) includes the well-known discretized mKdV lattice equation:
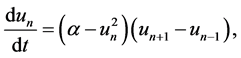(2)
where the subscript n in Equation (1) represents the 
lattice. Previously such equations have been studied using the Exp-function method [19] - [21] , the variational iteration method [22] , homotopy perturbation method [23] , homotopy perturbation transform method [24] and the homotopy analysis method [25] .
In this paper, we will study numerically Equation (2) using the mixture of new integral transform and homotopy perturbation method. It is worth mentioning that the proposed method is an elegant combination of the new integral transform, the homotopy perturbation method and He’s polynomials. The advantage of this technique is its capability of combining two powerful approaches for obtaining exact and approximate ana- lytical solutions for nonlinear equations. This method provides the solutions in terms of convergent series with easily computable components in a direct way without using linearization, perturbation or restrictive assumptions.
2. New Integral Transform
A new integral transform is derived from the classical Fourier integral. A new integral transform [26] was introduced by Artion Kashuri and Akli Fundo to facilitate the process of solving ordinary and partial differential equations in the time domain. Some integral transform methods such as Laplace, Fourier, Sumudu and Elzaki transforms methods, are used to solve general nonlinear non-homogenous partial differential equations with initial conditions and use fullness of these integral transform lies in their ability to transform differential equations into algebraic equations which allows simple and systematic solution procedures.
A new integral transform is defined for functions of exponential order. We consider functions in the set F defined as:
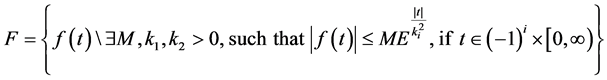(3)
For a given function in the set F, the constant M must be finite number, 
may be finite or infinite.
A new integral transform denoted by the operator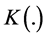 
is defined by:
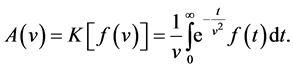(4)
For further detail and properties of this transform, see [26] - [28] .
3. Basic Idea of Mixture of New Integral Transform and Homotopy Perturbation Method
To illustrate the basic idea of this method, we consider a general nonlinear partial differential equation with the initial conditions of the form:
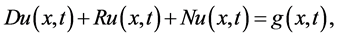(5)
(6)
where D is the second order linear differential operator
, R is the linear differential operator of less order than D, N represents the general nonlinear differential operator and 
is the source term.
Taking the new integral transform on both sides of Equation (5), we get
(7)
Using the differentiation property of new integral transform and above initial conditions (see Appendix), we have
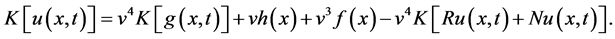(8)
Now, applying new integral transform on both sides of Equation (8), we get
![]()
(9)
where ![]()
represents the term arising from the source term and the prescribed initial conditions.
According to homotopy perturbation method, we have [27]
![]()
(10)
Now, by substituting
![]()
(11)
and
![]()
(12)
for some He’s polynomials ![]()
(see [29] [30] ) that are given by
![]()
(13)
in Equation (10), we get
![]()
(14)
which is the mixture of the new integral transform and the homotopy perturbation method using He’s polyno- mials. Comparing the coefficient of like powers of p, the following approximations are obtained.
![]()
Then the solution is:
![]()
(15)
4. Application
In this section, we apply the mixture of new integral transform and homotopy perturbation method to solve (2), subject to the initial condition
![]()
(16)
where d is an arbitrary constant.
Applying the new integral transform on both sides of (2) subject to initial condition (16), we have
![]()
(17)
The inverse new integral transform implies that
![]()
(18)
Applying the homotopy perturbation method, we get
![]()
(19)
where ![]()
are He’s polynomials that represent the nonlinear terms. The first few components of He’s polynomials are given by
![]()
(20)
Comparing the coefficients of like powers of p, we have
![]()
![]()
![]()
Therefore the approximate solution is
![]()
(21)
5. Numerical Result and Discussion
In this section, we calculate the numerical results of ![]()
for ![]()
and![]()
. Table 1 illustrates remarkable accuracy of the approximate solution. The comparison between mixture of new integral transform and the exact solution is performed in Figure 1. A very good agreement is achieved between the results obtained by the present method and the exact solution for different values of n.
![]()
Figure 1. Comparison between mixture of new integral transform (- - -, blue) and exact solution (---, red).
![]()
Table 1. The results of the mixture of new integral transform homotopy perturbation method and the exact solution, when ![]()
and![]()
.
6. Conclusion
In this paper, we have successfully proposed the mixture of new integral transform and homotopy perturbation method for solving discontinued problems arising in nanotechnology. The result shows that the given method is a powerful and efficient technique in finding exact and approximate solutions for nonlinear differential equa- tions. Also, it can be observed that there is good agreement between the results obtained using the present method and the exact solution. It is worth mentioning that the method is capable of reducing the volume of the computational work as compared to the classical methods while still maintaining the high accuracy of the numerical result; the size reduction amounts to an improvement of the performance of the approach.
Appendix
![]()
Table A1. Fundamental properties of a new integral transform of partial derivatives.