1. Introduction
“Current theory predicts that galaxies begin their existence as tiny density fluctuations, with overdensities collapsing into virialized protogalaxies, and eventually assemble gas and dust into stars and black holes” [1] . Steinhardt et al. [1] summarized data indicating that the current approach had difficulty accounting for massive galaxies and their associated central black holes at redshifts 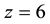 to
to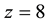 .
.
To address the “impossibly early galaxy problem” of Steinhardt et al., this analysis treats our universe as a closed Friedmann universe, dominated by vacuum energy in the form of a cosmological constant, and so large that it is approximately flat. This is consistent with full mission 2015 Planck satellite observations [2] indicating that the universe is dominated by vacuum energy, spatially flat to a good approximation, with Hubble constant , total matter density
, total matter density , and baryonic density
, and baryonic density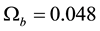 . Adler and Overduin [3] claimed “observation cannot distinguish―even in principle―between a perfectly flat universe and one that is sufficiently close to flat.” However, analysis assuming a closed inflationary universe and accounting for important features of large scale structure may indicate that our universe is closed.
. Adler and Overduin [3] claimed “observation cannot distinguish―even in principle―between a perfectly flat universe and one that is sufficiently close to flat.” However, analysis assuming a closed inflationary universe and accounting for important features of large scale structure may indicate that our universe is closed.
In the following, 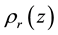 is the cosmic microwave background (CMB) radiation density at redshift z, where
is the cosmic microwave background (CMB) radiation density at redshift z, where 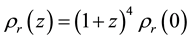 and the mass equivalent of today’s radiation energy density
and the mass equivalent of today’s radiation energy density  [4] , the matter density at redshift z is
[4] , the matter density at redshift z is 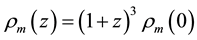 where
where 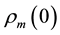 is today’s matter density, and
is today’s matter density, and
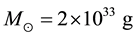 is the solar mass. With Hubble constant
is the solar mass. With Hubble constant , the critical density
, the critical density
 , where
, where 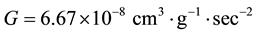 and
and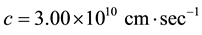 . Since
. Since
matter accounts for 30.8% of the energy in today’s universe, ![]() and the vacuum energy density
and the vacuum energy density![]() . The cosmological constant
. The cosmological constant
![]() and there is an event horizon in the universe at radius
and there is an event horizon in the universe at radius
![]() . According to the holographic principle [5] , the number of bits of information available on the light sheets of any surface with area a is
. According to the holographic principle [5] , the number of bits of information available on the light sheets of any surface with area a is![]() , where
, where ![]() is the Planck length and
is the Planck length and ![]() is Planck’s constant. So, only
is Planck’s constant. So, only ![]() bits of information on the event horizon will ever be available to describe our universe.
bits of information on the event horizon will ever be available to describe our universe.
In a closed universe, there is no source or sink for information outside the universe, so the total amount of information available to describe the universe remains constant. Also, after the first few seconds of the life of the universe, energy exchange between matter and radiation is negligible compared to the total energy of matter and radiation separately [6] . Therefore, in a closed universe, the total quantity of matter in the universe is conserved; there is only a fixed amount of information available; and the average mass per bit of information is constant. In a closed, isotropic, and homogeneous Friedmann universe, the constant mass per bit of information
(the mass ![]() within the event horizon today divided by the number of bits of
within the event horizon today divided by the number of bits of
information within the event horizon) is![]() . So, the total mass within the event horizon today relates to the square of the event horizon radius by
. So, the total mass within the event horizon today relates to the square of the event horizon radius by![]() , where
, where ![]() , giving the relation between mass within the event horizon and radius of a holographic screen just enclosing that mass.
, giving the relation between mass within the event horizon and radius of a holographic screen just enclosing that mass.
2. Galaxies at z = 6 to z = 8
At![]() , a hierarchical model of large scale structure can be developed using the holographic principle [7] , but the hierarchical model is not applicable at
, a hierarchical model of large scale structure can be developed using the holographic principle [7] , but the hierarchical model is not applicable at![]() . So, the following analysis extends the ideas in Refs. [7] to consider large scale structure at
. So, the following analysis extends the ideas in Refs. [7] to consider large scale structure at![]() .
.
When the matter density ![]() is much greater than the radiation density
is much greater than the radiation density![]() , the speed of pressure
, the speed of pressure
waves affecting matter density is ![]() [8] , and the Jeans’ length is
[8] , and the Jeans’ length is
![]() [8] . The Jeans’ mass, the mass of matter within a radius one quarter of the Jeans’ wavelength, is
[8] . The Jeans’ mass, the mass of matter within a radius one quarter of the Jeans’ wavelength, is![]() , where
, where![]() . Since
. Since ![]() is independent of z, the Jeans’ mass
is independent of z, the Jeans’ mass ![]() is independ- ent of z, and there are
is independ- ent of z, and there are ![]() Jean’s masses within the event horizon.
Jean’s masses within the event horizon.
In this holographic model for large scale structure at![]() , visible structures inhabit spherical isothermal halos of dark matter with masses ranging from that of the largest star to the Jeans’ mass, holographic radii
, visible structures inhabit spherical isothermal halos of dark matter with masses ranging from that of the largest star to the Jeans’ mass, holographic radii
![]() cm, the number
cm, the number ![]() of halos in mass bin
of halos in mass bin ![]() given by
given by![]() , and the number of bits of information in any mass bin (proportional to
, and the number of bits of information in any mass bin (proportional to![]() ) the same in all mass bins. Following Ref. [7] , this analysis
) the same in all mass bins. Following Ref. [7] , this analysis
uses a maximum stellar mass of ![]() [9] coinciding with the estimated minimum stellar mass at
[9] coinciding with the estimated minimum stellar mass at ![]() and consistent with indications that the first stars formed at
and consistent with indications that the first stars formed at ![]() [10] . The mass within the event
[10] . The mass within the event
horizon relates to the aggregate of halo masses by![]() . So,
. So, ![]() , the number of halos within the event horizon is
, the number of halos within the event horizon is ![]() and the average halo mass is
and the average halo mass is![]() .
.
While recognizing the difficulties and intricacies involved in estimating halo masses at large redshift, Steinhardt et al. [1] present their estimates for the number of halos in a volume ![]() in their Figure 1. For comparison with those data, consider mass bins with width
in their Figure 1. For comparison with those data, consider mass bins with width![]() . Then, within the volume now enclosed by the event horizon, the number of halos with mass between
. Then, within the volume now enclosed by the event horizon, the number of halos with mass between ![]() and
and
![]() is
is![]() . Correspondingly, the number of halos with
. Correspondingly, the number of halos with
mass between ![]() and
and ![]() is
is ![]() and the number of halos with mass
and the number of halos with mass
between ![]() and
and ![]() is
is![]() .
.
The scale factor ![]() relates to today’s scale factor
relates to today’s scale factor ![]() by
by![]() . The volume within the event horizon today,
. The volume within the event horizon today, ![]() , occupied a volume of
, occupied a volume of ![]() at
at ![]() and a volume of
and a volume of
![]() at
at![]() . So, the volume within the event horizon today was
. So, the volume within the event horizon today was ![]() at
at![]() , and
, and ![]() at
at![]() . Considering mass bins with width
. Considering mass bins with width![]() , the number of halos per
, the number of halos per ![]() and the logarithm of that density expected from this holographic model for
and the logarithm of that density expected from this holographic model for ![]() and
and ![]() are shown below.
are shown below.
Compared to the cloud of data points in Figure 1 of Steinhardt et al. [1] showing their estimated halo densities, the above results are slightly below the cloud at![]() , just below the lower edge of the cloud at
, just below the lower edge of the cloud at![]() , and at the upper edge of the cloud at
, and at the upper edge of the cloud at![]() . So, halo densities similar to those estimated from observations at
. So, halo densities similar to those estimated from observations at ![]() to
to ![]() are an inevitable consequence of the holographic anlysis outlined above.
are an inevitable consequence of the holographic anlysis outlined above.
3. Black Holes at z = 6 to z = 8
As in Ref. [7] , it is assumed an isothermal spherical halo of dark matter with mass MS is enclosed by a holo-
graphic screen with radius ![]() cm. The isothermal halo matter density distribution is
cm. The isothermal halo matter density distribution is![]() ,
,
where r is the distance from the center of the halo and a is constant. The mass ![]() within the holographic
within the holographic
radius Rs in an isothermal density distribution is![]() , requiring
, requiring![]() . The mass within radius R from the center of a halo is
. The mass within radius R from the center of a halo is![]() .
.
If the mass of the central supermassive black hole (SMBH) is at the center of a core volume with radius ![]() equal to the holographic radius of stars with the maximum stellar mass, stars of all masses can orbit the center of the structure just outside the core without their holographic screens encountering the central black hole so they would be disrupted and drawn into the central black hole. The resulting SMBH mass estimate is
equal to the holographic radius of stars with the maximum stellar mass, stars of all masses can orbit the center of the structure just outside the core without their holographic screens encountering the central black hole so they would be disrupted and drawn into the central black hole. The resulting SMBH mass estimate is
![]() , where
, where ![]() is the total halo mass and
is the total halo mass and ![]() is the maximum stellar mass.
is the maximum stellar mass.
Mortlock et al. [11] found a black hole with mass ![]() at
at ![]() in the quasar ULAS J1120+ 0641. Pacucci, Volonteri, and Ferrara [12] , noting evidence for supermassive black holes in the
in the quasar ULAS J1120+ 0641. Pacucci, Volonteri, and Ferrara [12] , noting evidence for supermassive black holes in the ![]() to
to ![]() range only 109 years after the Big Bang, recognize this “evidence contrasts with the standard theory of black hole growth.” In comparison, the average halo mass at z = 6 to z = 8 in this holographic model is
range only 109 years after the Big Bang, recognize this “evidence contrasts with the standard theory of black hole growth.” In comparison, the average halo mass at z = 6 to z = 8 in this holographic model is ![]() and the corresponding central black hole mass is
and the corresponding central black hole mass is![]() , similar to the mass of the black hole in ULAS J1120 + 0641.
, similar to the mass of the black hole in ULAS J1120 + 0641.
4. Conclusion
Caltech’s Professor Steinhardt and colleagues [1] discussed the “impossibly early galaxy problem,” reviewing data showing that the conventional approach to formation of large scale structure cannot adequately account for presence of the massive galaxies and associated central black holes observed at redshifts z = 6 to z = 8. In sharp contrast, the holographic analysis outlined above requires supermassive black holes with mass on the order of ![]() at z = 6 to z = 8. This is consistent with the observations of Trakhtenbrot et al. [13] indicating the presence of a black hole with mass
at z = 6 to z = 8. This is consistent with the observations of Trakhtenbrot et al. [13] indicating the presence of a black hole with mass ![]() in the AGN (active galactic nucleus) CID-947 at
in the AGN (active galactic nucleus) CID-947 at![]() .
.