Portfolio Management: Stock Ranking by Multiple Attribute Decision Making Methods ()
1. Introduction
Nowadays, due to the complexity and diversity involved in investments, the evaluation and ranking of companies is an important issue. It is necessary to promote a method for identifying efficient and superior firms. Ranking of stocks differentiates efficient companies from non-efficient ones. In order to optimize the return, effective selection process of stocks for portfolio investments is one of the most important decision making processes in competitive capital markets. Several researchers have investigated the problem with different perspectives.
Quah (2008) presented methodologies to select equities based on soft-computing models which focus on applying fundamental analysis for equities screening and compared the performance of three soft-computing models [1] . The methods used were multi-layer perceptions (MLP), adaptive neuro-fuzzy inference systems (ANFIS) and general growing and pruning radial basis function (GGAP-RBF).
Fatma Tiryaki and Beyza Ahlatcioglu (2009) used the fuzzy AHP for the portfolio selection problem [2] . The authors considered a hierarchy of factors with extrinsic, intrinsic and investor’s objectives at the top level. Extrinsic factors consist of economic, political and technological factors. Profitability, size and technology are the intrinsic factors. Profitability, security, excitement and control are generally the investor’s objectives. Naser Jamshidi and Mahmood Ramshini (2014) have made ranking of automotive and petrochemical companies by using combined approaches of FAHP-TOPSIS and FAHP-DEA method [3] . Hasan Dincer (2015) proposed a profit based stock selection model by Fuzzy AHP and MOORA (the Multi-Objective Optimization by Ratio Analysis) methods and applied it on banking stocks listed at Borsa, Istanbul Stock Exchange [4] . Majid Moradi and Hossein Janatifar (2014) have proposed a framework based on the Fuzzy Multiple Criteria Decision Making (FMCDM) approach for ranking firms of automobile companies listed in Tehran Stock Exchange by using financial ratios [5] . The approach relies on TOPSIS method.
Sevastjanov Pavel and Dymova Ludmila (2009) suggested a new method for stock screening with the use of multiple criteria decision making and optimization [6] . The method considers financial indices and market success of a firm. It selects the stocks with a great correlation between the two. However, the complexity can be reduced if stock price is also considered as one of the attributes with higher weight compared to other attributes. Kao-Yi Shen, Min-Ren Yan and Gwo-Hshiung Tzeng (2014) have proposed an MADM method for solving glamor stocks (value investing and growth stocks) selection problem based on fundamental analysis [7] . The method is a blending of VIKOR method and DANP (Decision Analytical Network Process).
Ricardo Giglio and Sergio Da Silva (2009) have proposed ranking of the stocks listed on Bovespa Stock Exchange according to their relative efficiency based on the algorithmic complexity theory [8] . It does not consider any of the financial ratios in ranking the stocks. Pinporn Maikaew and Patcharaporn Yanpirat (2012) have proposed a multiple criteria stock ranking model and tested it on the stocks listed at the Stock Exchange of Thailand (SET 100) by using TOPSIS method [9] .
The efficient portfolio can only be built when the stocks in the portfolio constitute a right mix. Therefore, selection of the best stock among the existing ones in the same industry becomes crucial. Accordingly, there is a need for a study to provide a mechanism for performance evaluation. This paper intends to develop a decision making method to assign ranks to the companies (alternatives) on the basis of several financial and non-financial (quantitative and qualitative) parameters (attributes) which affect the performance of the company. Owing to the regulator SEBI (Securities and Exchange Board of India) investors can access all the information and data of the listed companies. All the data considered in this paper is available at www.nseindia.com.
Three kinds of analyses, namely, technical analysis, bottom-up analysis, and social analysis help us understand where the company ranks among its peers. Stock price is a good indicator of a company’s financial health, if not driven by rumors or speculation. Speculation in the prices of a stock is measured by the value of beta. It is an indicator of a stock’s standard deviation, or volatility. For a technical analyst, this volatility is of worth as traders prefer stocks with high beta. But for investment purposes, fundamentals of a company, i.e. bottom-up and social analysis, should be taken into account. The present work deals with the selection of stocks for investment purpose. So, in this work, higher values of beta are discouraged by giving it smaller weightage. Basically, earnings drive stock prices. Several financial ratios, such as total income, net profit, operating profit margin, net profit margin, are useful to measure the earnings. Investors can compare these financial ratios of a company with those of other companies in the same sector. Dividends and bonus are the rewards by the companies to their shareholders for holding their stocks. Warren Buffett prefers to buy or sell a company’s stock based on its intrinsic value. Net worth and return on net worth are the indicators of the intrinsic value of a company. Promoter holding and FII + DII holding reflect the confidence of promoters and of high net worth investors respectively. Reliability is a qualitative attribute, to some extent, subjective also, in the selection process. It is based on the brand value of the products and/or services offered by the company as well as quality of the management. The effects of some of the attributes such as book value of a stock, earnings per share are reflected in the attributes, namely, net worth and net profit respectively. So, they need not to be considered separately as attributes.
The proposed method is validated by considering the data for 13 Indian IT companies for last five years [NSE]. The companies considered are TCS, HCL Tech, Wipro, Persistent Systems, Mphasis, Hexaware, Vakrangee, Infosys, KPIT Tech, Zensar Tech, NIIT Tech, Sonata Software, Mastek, in this order. The results obtained are matched with the general opinions of informed investors. As the fluctuations of currency affect every company of the IT sector and its effect will appear in net profit numbers, it is not considered as a separate attribute. The data used for promoter holding and FII + DII holding as well as bonus must be recent. However, the fluctuations in rest of the data are smoothed by taking average of five years of these data. Reliability is assigned a value in the scale of 1 to 9, the smaller the number, the lesser the reliability.
MADM is an approach employed to solve problems involving selection from among a finite number of alternatives. There are numerous applications of these methods in management science, economics, psychometrics, marketing research, applied statistics, decision theory, and many more to name a few. Of the many MADM methods, the following four commonly used methods are considered in this work.
1) Simple Additive Weight method (SAW);
2) Analytic Hierarchy Process method (AHP);
3) Technique for Order Preference by Similarity to Ideal Solution (TOPSIS);
4) Compromise Ranking method (or VIsekriterijumskoKOmpromisnoRangiranje―VIKOR).
In TOPSIS method, the distances are generalized as p-norms. In VIKOR method also, generally researchers fix the value of p as 1. In both these cases, several values of p are tested in the range [1, ∞] and their effects are examined. Critic method is used to find weight vector in TOPSIS method and eigenvalue method is used in AHP method. The GUI system developed incorporates all the above methods and assigns ranks to the companies as per the user’s choice of method.
To the best of our knowledge the present is the first report on employing MADM methods for ranking of Indian stocks.
2. MADM Methods
In 1947, a book “Theory of Games and Economic Bahavior” published by von Neumann and Morgenstern opened the door to Multiple Attribute Decision-making Methods (MADM) [10] . In 1957 it was Churchman, Ackoff and Arnoff who first treated a MADM for selecting business investment policy using simple additive weighting (SAW) method [11] . MADM methods are generally discrete, with a limited number of predetermined alternatives. An MADM method specifies how attribute information is to be processed in order to arrive at a choice. Each decision table (also called decision matrix) in MADM methods has four main parts, namely: 1) alternatives, 2) attributes, 3) weight or relative importance of each attribute, and 4) measures of performance of alternatives with respect to the attributes. The decision matrix is shown in Table 1.
2.1. The SAW Method
The Simple Additive Weighting (SAW) method is probably the best known and widely used method for MADM. Here each attribute is given a weight, and the sum of all weights must be equal to 1. Each alternative is assessed with regard to every attribute. The composite performance score which determines the ranking is given by
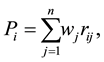
where  is the normalized preferred ratings of the
is the normalized preferred ratings of the  alternative with respect to the
alternative with respect to the  criterion, given by, for beneficial
criterion, given by, for beneficial 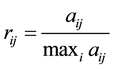 and for non-beneficial
and for non-beneficial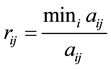 , for
, for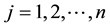 .
.
2.2. The AHP Method
The analytic hierarchy process (AHP) is a structured technique for organizing and analyzing complex decisions, based on mathematics and psychology. It was developed by Thomas L. Saaty in the 1970s [12] [13] . The method first compares the attributes pair wise by assigning intensity of importance in the scale of 1 (equal importance) to 9 (extreme importance). Denoting n elements to be compared as  and the relative priority of
and the relative priority of 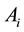 with respect to
with respect to 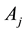 by
by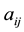 , a matrix
, a matrix 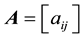 of order n can be formed, called reciprocal matrix, where
of order n can be formed, called reciprocal matrix, where
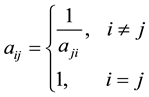
The n elements  need to be assigned a set of numerical weights
need to be assigned a set of numerical weights ![]() which allows diverse elements to be compared to one another in a rational way. In the ideal case, the relation between weights
which allows diverse elements to be compared to one another in a rational way. In the ideal case, the relation between weights
![]() and
and ![]() is given by
is given by![]() .
.
The matrix ![]() is called consistent if its elements are transitive i.e.
is called consistent if its elements are transitive i.e. ![]() for all i, j, k. For a reciprocal matrix
for all i, j, k. For a reciprocal matrix![]() ,
,![]() ; with equality if and only if
; with equality if and only if ![]() is consistent, where
is consistent, where ![]() is the maximum ei-
is the maximum ei-
genvalue of![]() . The consistency index (CI) is the value
. The consistency index (CI) is the value![]() . The random index (RI) is defined as the av-
. The random index (RI) is defined as the av-
erage CI calculated from a large number of randomly generated reciprocal matrices. The consistency ratio (CR)
of a reciprocal matrix ![]() is defined as
is defined as ![]() by T. Satty in 1990. Usually, a CR of 0.1 or less is considered as
by T. Satty in 1990. Usually, a CR of 0.1 or less is considered as
acceptable, and it reflects an informed judgment attributable to the knowledge of the analyst regarding the problem under study. J. Alonso and M. Lamata derived the equation ![]() where
where![]() , as an alternative criterion to verify the condition
, as an alternative criterion to verify the condition ![]() by taking the average of 500000 randomly generated reciprocal matrices [14] .
by taking the average of 500000 randomly generated reciprocal matrices [14] .
2.3. p-TOPSIS Method
The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) is a multi-criteria decision analysis method, which was originally developed by Hwang and Yoon in 1981 with further developments by Yoon in 1987, and Hwang, Lai and Liu in 1993 [15] [16] . The basic concept of this method is that the selected alternative should have the shortest distance from the ideal solution and the farthest distance from the negative- ideal (anti-ideal) solution in some geometrical sense.
As an illustration, Figure 1 shows five alternatives, A, B, C, D and E, with two criteria; it also shows the ideal and anti-ideal points. Obviously, in case of the usual Euclidean distance (p = 2) with equal weights, point C is the closest to the ideal and D is the longest. The method can be outlined as follows.
1) Let ![]() be the
be the ![]() decision matrix and
decision matrix and ![]() be its normalization.
be its normalization.
2) Construct the weighted normalized decision matrix![]() .
.
3) Determine ideal and negative-ideal solutions.
Let ![]() and
and
![]()
Determine the worst alternative ![]() and the best alternative
and the best alternative ![]() as under:
as under:
![]()
![]()
4) The TOPSIS method evaluates the separation measures by considering l2-norm. One of the contributions in this paper is to define generalized separation measures using lp-norm with real ![]() as distance metrics and study its effect on ranking.
as distance metrics and study its effect on ranking.
![]() (1)
(1)
![]() (2)
(2)
Also, for![]() , the separation measures with L¥-norm is defined as
, the separation measures with L¥-norm is defined as
![]() (3)
(3)
![]() (4)
(4)
5) The relative closeness to the ideal solution, which will be used for the ranking of options, is calculated as in formula
![]() (5)
(5)
Clearly,![]() . Rank the alternatives according to the value of
. Rank the alternatives according to the value of![]() . In this paper, the method proposed is referred to as p-TOPSIS.
. In this paper, the method proposed is referred to as p-TOPSIS.
An attempt has also been made to modify this method by using weighted Euclidean distances, rather than creating a weighted decision matrix, referred to as modified TOPSIS method, by Deng et al. (2000) [17] . In this paper, all three methods, namely, TOPSIS, modified TOPSIS and p-TOPSIS, are implemented.
2.4. p-VIKOR Method
VIKOR method was developed for multicriteria optimization of complex systems. It was originally developed by Serafim Opricovic to solve decision problems with conflicting and non-commensurable (different units) criteria in his Ph.D. dissertation in 1979 [18] , and an application was published in 1980. The idea of compromise solution was introduced in MCDM by Po-Lung Yu in 1973 and by Milan Zeleny [19] [20] . Let ![]() and
and ![]() if the
if the ![]() function is benefit and
function is benefit and ![]() and
and ![]() if the
if the ![]() function is cost. The compromise ranking algorithm VIKOR consists of the following steps:
function is cost. The compromise ranking algorithm VIKOR consists of the following steps:
1) The first step is to determine the objective, and to identify the pertinent evaluation attributes. Determine the best ![]() and worst
and worst ![]() values of all criterion functions,
values of all criterion functions,![]() .
.
2) Compute the values ![]() and
and![]() ,
, ![]() by the relation
by the relation
![]() (6)
(6)
![]() (7)
(7)
3) Compute the value ![]() by the relation
by the relation
![]()
where![]() . Here v is introduced as weight of the strategy of the majority of attributes. Usually, the value of v is taken as 0.5. However, it can take any value from 0 to 1.
. Here v is introduced as weight of the strategy of the majority of attributes. Usually, the value of v is taken as 0.5. However, it can take any value from 0 to 1.
4) Rank the alternatives. Sort the values of S, R and Q in decreasing order. The results are three ranking lists. The compromise ranking list for a given v is obtained by ranking with ![]() measures. The best alternative is the one with the minimum value of
measures. The best alternative is the one with the minimum value of![]() .
.
5) For given attribute weights, propose a compromise solution, alternative![]() , which is the best ranked by measure Q, if the following two conditions are satisfied:
, which is the best ranked by measure Q, if the following two conditions are satisfied:
a) Acceptable advantage:![]() , where
, where ![]() is the second best alternative in the ranking by Q.
is the second best alternative in the ranking by Q.
b) Acceptable stability in decision making: Alternative ![]() must also be the best ranked by S or/and R.
must also be the best ranked by S or/and R.
This compromise solution is stable within a decision making process, which could be: voting by majority rule (when ![]() is needed) or by consensus (when
is needed) or by consensus (when![]() ) or with veto (when
) or with veto (when![]() ).
).
Usually, researchers take the value of p as 1. In this paper, other values of p have also been tried.
2.5. Estimation of Weights
If the criteria are assigned weights as per the choice of decision maker, the subjectivity enters into the picture. This may result into misleading conclusions. One of the ways to remove this subjectivity is to assign data-de- pendent weights. In the present implementation, a method, called critic method, suggested by H. Kazan has been used in the TOPSIS method. Similarly, one of the several methods discussed for assigning objective weights, namely eigenvalue method, is used in AHP method by S. Gao [21] .
In critic method [22] , both standard deviation of the criterion and its correlation among other criteria are included in the weighting process. Let ![]() be the standard deviation of the
be the standard deviation of the ![]() criteria and
criteria and ![]() be the correlation coefficient between the
be the correlation coefficient between the ![]() and
and ![]() criteria.
criteria.
The weight ![]() of the
of the ![]() criteria is obtained by
criteria is obtained by
![]()
where ![]() is defined as
is defined as
![]() (8)
(8)
3. Results
The GUI software, incorporating some of the known methods and modifications suggested in this paper, makes it possible to select a small group of “good” stocks (and to reject a small group of “inferior” stocks) on the basis of different types of meaningful financial ratios considered. The results are presented in the following Table 2. Note that the results for only two values of p are displayed in the Table 2, but other values of p can also be tried for in case of p-TOPSIS and VIKOR method. Though the actual ordering of the better performing companies and inferior performing companies differ for different methods, it can be observed that they remain same with some exceptions. As an example, 2nd company is selected by all the methods. Similarly, 6th company is not selected by only one method, namely, AHP. 4th company is selected as an exception by VIKOR method that can be neglected. Similar comments apply to the rejection of inferior companies. For example, 13th and 5th companies are declared as inferior companies by all the methods.
As far as effects of varying p are considered, the p-TOPSIS method exhibits the uniform ranking for p in the range [1] [16] , exhibiting stability of ranking over considerably large value of p. However, larger values of p results into absurdity. Similarly, VIKOR method also gives satisfactory result for p in [1] [2] only. To arrive at some general conclusion, further experimentation with other companies of different sectors may be performed. Of course, in that case, one may have to rethink about the attributes considered.
Selected screen shots as in Figures 2-4 show the actual execution process. The upper table titled “Company Information” contains the collected data which remains fixed. The column titles indicate the attributes. The attributes considered along with their abbreviations are: Total Income (TI), Net Profit (NP), Net Worth (NW), Return on Net worth (RON), Stock Price (SP), Promoter Holding (PH), FII + DII Holding (FII), Operating Profit Margin (OPM), Net Profit Margin (NPM), Dividend Payout Ratio (DPR). The user has to just select the
![]()
Figure 2. Ranking by p-TOPSIS method (p = 4.5).
![]()
Figure 4. Ranking by p-VIKOR method (p = 2).
method among the methods listed in the table “Select the Method”. If the method requires the value of p, then a separate box will be displayed asking the user to enter the value. After this, when the user clicks the button “Decision Maker”, the results are displayed in the table titled “Output” and the four good and four inferior companies are displayed at proper place.
4. Conclusion
Collective performance assessment of n entities in the context of chosen n attributes is an important aspect in decision making in finance, engineering, social sciences, management, etc. There are several methods, called multiple attribute decision making methods, developed for this purpose. In the present note by replacing Euclidean norm by the p-norms, 1< p < ∞ in Rn, we have modified two of these methods: TOPSIS method and VIKOR method into p-TOPSIS and p-VIKOR methods respectively. We analyze performance of 13 companies of IT sector listed on Indian Stock Exchanges considering 13 financial and non-financial attributes using each of the MADM methods, namely, SAW, AHP, p-TOPSIS, p-VIKOR (with different values of p).
We concentrate on ranking of the first four best performing companies and the last four worst performing companies to assess stability of these methods for different values of p. It is found that for values of p in the interval [1] [16] , this ranking by and large remains the same in p-TOPSIS method. In p-VIKOR method, more or less same conclusion is obtained for values of p in the interval [1] [2] . This exhibits stability of these methods with respect to p. We have also considered comparative ranking of these companies with other MADM methods. By and large, comparison shows that the first four ranks (as well as last four ranks) are just the permutations of the same numbers.
As a way forward, other MADM methods such as ELECTRE, PROMETHEE, COPRAS will be tried for. Similarly, to delve into the ranking of entities of other asset classes is also an interesting idea. To devise a completely new method for the purpose may be considered as an excellent contribution to the theory of MADM methods.
Acknowledgements
The authors are thankful to Prof. S. J. Bhatt for suggesting p-TOPSIS method and for reading the manuscript. The work is supported by UGC-SAP-DRS-F.510/1/DRS-III/2015 (SAP), to the Department of Mathematics, S P University.
NOTES
*Corresponding author.