Finite Temperature Asymmetric Nuclear Matter Using Pion Dressing ()
1. Introduction
The properties of hot dense nuclear matter are very important in the context of neutron stars [1] as well as in high-energy heavy-ion collisions experiments. In those experiments, nuclei undergo collisions [2] and produce states of nuclear matter at different temperatures at conditions far from those normally encountered in low energy collisions. At low temperatures, this can be attained in medium energy heavy-ion reactions; no such exotic state can be produced but there is the possibility of interesting liquid-gas phase transitions leading to the breakup of heated nuclei into small clusters or droplets of nucleons [3] .
Such phase transitions have been identified in multifragmentation experiments and in the crusts of neutron stars [4] [5] . The possibilities of such phase transitions were previously considered by several authors using different approaches [6] - [8] . Walecka [9] in a attempt, developed a method consisting of interactions of nucleons with a neutral scalar field σ and ρ mesons as well as neutral vector meson ω. Variations of the same model have also been considered including cubic and quartic terms in the σ fields to reproduce correct bulk modulus of nuclear matter [10] . These calculations however use meson fields as classical, and use a σ-field which is not observed.
A model for infinite nuclear matter consisting of interacting nucleons and pions was considered in [11] . The Pion Nucleon interaction was taken with off mass shell of pion. The scalar isoscalar pion condensates simulated the effects of σ mesons [12] with the short distance repulsion arising from composite structure of nucleons and/or through vector meson exchanges. This appeals aesthetically as classical σ fields arise from quantum mechanical structures and also has a stronger phenomenological appeal as σ mesons have not been found in nature. With a similar approach we shall reconsider nuclear matter at finite temperatures with pion dressing [13] with off mass shell. The methods of thermofield dynamics [14] fit naturally for this purpose because here statistical average is done through an expectation value over a “thermal vacuum” [11] in an extended Hilbert space.
The article is organised as follows. In Section 2, we review the thermofield dynamics to consider hot and dense nuclear matter and obtain expressions for temperature-dependant pressure P, binding energy B and nuclear density ρ. In Section 3, we evaluate numerically the above applying variational technique, study their characteristics and discuss the results so obtained.
2. Formalism
We consider the effective Hamiltonian for pion nucleon interaction at zero temperature [15] -[17] as
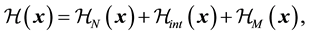(1)
where
, 
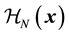and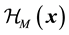 
are the Hamiltonians for the free nucleon part, the pion-interaction part and the free meson part respectively. Here 
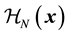is given by
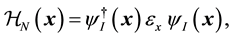(2)
and the effective Hamiltonian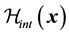 
for pion nucleon 
interaction
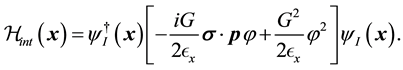(3)
We have taken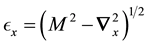
, with M as the mass of the nucleon. The free meson part of the Hamiltonian is given by
(4)
where 
denotes the mass of the meson and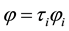
. The pion field expansion in Equation (4) in terms of annihilation and creation operators is given by
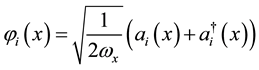
(5)
with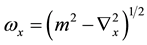
. We now study asymmetric nuclear matter at finite temperature using thermofield dynamics method. Here the thermal average of a quantum operator ![]()
given in [13] [14] with![]()
, as
![]()
(6)
The above reduces to ground state expectation, in zero temperature limit value for the operator![]()
, shown below as
![]()
(7)
where ![]()
is the lowest energy state. In thermofield method, one generalises [13] to the case of finite temperature and for some![]()
, the relationship holds
![]()
(8)
where ![]()
is defined as the “thermal vacuum”. Here corresponding to physical operator a, a “tilde” operator ![]()
is introduced to denote thermal modes. At finite temperature the ground state is replaced by ![]()
given as [13]
![]()
(9)
where ![]()
in the above corresponds to the extra Hilbert space. The function ![]()
is calculated through minimization of thermodynamic potential density given as
![]()
(10)
where![]()
, the chemical potential, N, number of nucleons and the entropy density
![]()
For zero chemical potential and for free fields, extremization of the free energy then yields
![]()
(11)
with Hamiltonian density as ![]()
![]()
so that
![]()
If we substitute this value the free energy density becomes
![]()
Similarly for the fermionic sector the thermal vacuum is
![]()
(12)
where ![]()
corresponds to the creation of the fermionic thermal modes. The entropy is given as
![]()
and ![]()
is given as [13]
![]()
(13)
where ![]()
is the chemical potential corresponding to baryon number conservation and ![]()
for free fermions of mass M. In this methodology the correct distribution function with extra thermal modes can be obtained and this enables us to have the temperature dependent background off-shell pion pair configuration given as
![]()
(14)
with
![]()
(15)
and
![]()
(16)
In the above,
![]()
(17)
In nucleon sector for fermions
![]()
(18)
with
![]()
(19)
where ![]()
will be determined later. We then have the nuclear matter density
![]()
(20)
Here the thermodynamic potential [18] is given by
![]()
(21)
where ![]()
and ![]()
are chemical potentials of proton and neutron respectively, ![]()
and ![]()
are neutron and proton densities and S is the entropy of the asymmetric nuclear matter![]()
. Clearly, with ![]()
, Equation (13) gives ![]()
of zero temperature. ![]()
for the interacting system will be determined here from the construction of the thermodynamic potential. We thus have for the nucleon kinetic term temperature dependent as
![]()
(22)
The temperature dependent kinetic energy due to the mesons is given by
![]()
(23)
where ![]()
and ![]()
is pion dressing function [13] which extremises energy, pressure and entropy etc of nuclear matter. Then the interaction energy density becomes
![]()
(24)
where
![]()
(25)
we shall now assume a phenomenological term corresponding to meson repulsion due to composite structure of mesons given as
![]()
(26)
Finally, the nucleon repulsion term given as
![]()
(27)
where ![]()
is as given in Equation (20). Thus the energy density is given by
![]()
(28)
where
![]()
as before.
The thermodynamic potential density Ω is given by
![]()
(29)
where the last term corresponds to nucleon number conservation with ![]()
and ![]()
as the chemical potentials of proton and neutron respectively. The temperature dependent pressure is given as![]()
. The entropy density above is ![]()
with ![]()
being the entropy in fermion sector given as
![]()
and similarly the meson sector contribution ![]()
is given as
![]()
Thus the thermodynamic potential density now is a functional of![]()
, ![]()
as well as the pion dressing function ![]()
which will of course depend upon temperature. Extremisation of Equation (29) with respect to ![]()
yields
![]()
(30)
which is of the same form as [16] for zero temperature. Similarly minimising the thermodynamic potential with respect to ![]()
we get
![]()
(31)
where
![]()
(32)
Once we substitute the optimised dressing as in Equation (30), the above simplifies to
![]()
(33)
which is different from ![]()
due to interactions. Further, minimising the thermodynamic potential with respect to ![]()
we have the solution
![]()
(34)
with
![]()
(35)
where J is given in Equation (25). We may note that the change in ![]()
above from ![]()
is also due to interaction.
3. Results and Discussions
The parameters a, ![]()
, ![]()
and ![]()
[15] [16] are determined variationally. The first three of these four parameters are evaluated by constraining the binding energy per nucleon![]()
, the pressure P and the
compressibility K of the symmetric nuclear matter i.e.![]()
, ![]()
and ![]()
[19] .
The fourth parameter ![]()
of our calculation is evaluated by fixing the value of ![]()
to the standard value of 31 MeV.
The pion-nucleon coupling constant ![]()
and a = 115.264 MeV, ![]()
, ![]()
and![]()
.
In Figure 1 we study the nature of variation of EB with different baryon densities at different temperatures. The saturation binding energy increases from −16 MeV at zero temperature to higher values with rise of temperature. This clearly shows that the temperature has a significant effect on symmetric nuclear matter.
In Figure 2, the variation of pressure P with nucleon densities have been studied at different temperatures (T = 0, 4, 8, 12, 16, 20 MeV). It shows that at the saturation density, the pressure is zero for zero temperature as usual. But pressure becomes negative if one goes towards lower density and it becomes zero at zero nuclear density. This peculear behaviour is first order phase transition. This trend disappears at higher temperatures.
In Figure 3, the variation of pressure with nucleon densities for different Proton fraction at different temperatures. It shows that at Proton fraction ![]()
the pressure becomes positive. If one goes to higher yPs the Pressuer becomes negative at different lower densities reaching zero Pressure at zero nucleon densities. So the
![]()
Figure 1. The binding energy EB as a function of nucleon density ρ.
![]()
Figure 2. The pressure P as a function of nucleon density ρ at different temperature.
asymmetric nuclear matter behaves differently at different nucleon densities.
In Figure 4, the slope ![]()
at different relative nucleon densities ![]()
are plotted at two different
temperatures for different proton fractions. It shows that the slope becomes negative as the relative nucleon densities increases to a certain value and then increases at higher values. The trend is same at different higher temperatures but terminates to a certain value of slope at certain lower densities.
4. Summary
In this paper, we study the warm equation of state (EOS) of asymmetric nuclear matter taking pion-nucleon interaction with repulsive effect due to ρ and ω mesons. We observe here that our results are comparable with the Non-Linear Walecka (NLWM) and Quark Meson Coupling (QMC) model [20] . The binding energy changes from negative to positive value with increase of temperature around saturation density. The profile of pressure variation with density at different temperatures shows that there is a liquid-gas phase transition and the transition
![]()
Figure 3. The pressure P as a function of nucleon density ρ for different proton fraction.
![]()
Figure 4. The pressure variation ![]()
as a function of relative nucleon density ![]()
for different proton fraction.
is continuous above the critical temperature Tc at which![]()
. We also observe that the pressure gradient becomes more negative due to increase of proton fraction leading to a possibility of instability.