1. Problem Formulation
In this paper, the realization of an aerodynamic brake integrated in a rear wing of a formula car has been considered. The first step consists in the choice of an appropriate aerodynamic appendix. In particular, it was decided to study an Italian Formula 4 race car [1] , being a category in the first stages of development. Also, the regulation of this championship is easy to find and the car is characterized by uniformity of the mechanics and the airfoils. Therefore, taken note of the technical regulation on FIA website, it was decided to study the upper airfoil, of which was shown a dimensioned drawing (Figure 1). It is an aluminum alloy wing, with a chord line of 237.9 mm and a height of 54.2 mm.
Formula 4 championship will provide the use of a 4T heat engine (Otto/Beau de Rochas cycle): it can be naturally aspirated or turbocharged, with maximum power in the order of 120 kW (160 HP). Considering the weight of the car and the race tracks of the championship, it is predicted a maximum speed of 230 km/h (64 m/s). Regarding the operating conditions, an air temperature of 300K was assumed at atmospheric pressure.
Briefing Description of Airfoil Behavior
Considering an airfoil, there are several elements that have a specific nomenclature:
1) Mean camber line: locus of points halfway between the upper and lower surface as measured perpendicular to the mean chamber line itself;
2) Leading edge: the most forward point of the mean camber line;
3) Trailing edge: the rearmost point of the mean camber line;
4) Chord: the straight line joining the leading edge with the trailing edge;
5) Upper surface: the upper boundary of the profile;
6) Lower surface: the lower boundary of the profile;
7) Thickness: the distance between the lower surface and the upper surface.
The different airfoil shapes are marked by a logical numbering system which was introduced by the U.S. federal agency NACA. This system consists of four digits which have a definite meaning:
・ the first digit indicates the maximum camber in hundredths of chord;
・ the second digit represents the location of maximum camber along the chord from leading edge in tenths of chord;
・ the third and fourth give the maximum thickness in hundredths of chord.
When an airfoil is moving relative to the air, it generates an aerodynamic force, in a rearward direction at an angle with the direction of relative motion. This aerodynamic force is commonly resolved into two components: lift and drag. Lift is the force component perpendicular to the direction of relative motion while Drag is the force component parallel to the direction of relative motion. These forces are studied at different angles of attack which is the angle at which an airfoil cleaves fluid. The experimental data show that CL varies with the angle of attack: more precisely, at low angles of attack the lift coefficient CL varies linearly with α. In a region characterized by a linear trend, the flow moves smoothly over the airfoil and is attached to the back of the wing. As soon as α increases, the flow tends to separate from the surface of the airfoil, creating a region of “dead air” behind the profile. A briefing flow analysis of the physical phenomenon in question in order to understand better what is happening in the latter case is reported. It is clear from Figure 2 that the speed at the trailing edge tends to increase, with a strong reduction of the pressure, while in the stagnation point the speed tends to be zero and pressure rises sharply. It creates an adverse pressure gradient, thus particles of fluid move from the trailing edge to the stagnation point, and then it has a rapid separation of the boundary layer below. Stagnation point does not have a stable position in these conditions because there is not pressure recovery. The recirculation generated by
![]()
Figure 1. Dimensioned Drawing of a F4 rear wing (in mm).
![]()
Figure 2. Airfoil characteristics with generic flow direction.
the detachment of the boundary layer creates first vortex that causes a wake vortex. It is necessary to study the turbulent behavior of the fluid that meets the wing, through the Navier-Stokes equations in order to consider the stall of the wing:
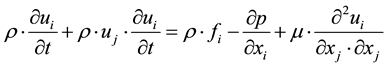 (1)
(1)
where u(x, t) is the instantaneous velocity, ρ the medium density, μ the viscosity and f the applied force.
This system of equations is a system of partial differential equations that describe the behavior of a Stokesian fluid: the fluid can be considered to be continuous. There is an analytical solution only in simplified cases, while solutions in the other cases can be obtained using simplified methods of numerical analysis. The most straight- forward method for the numerical simulation of turbulent flows is direct numerical simulation DNS which discretizes the Navier-Stokes equations. It resolves the entire range of turbulent length scales thus the description of the flow is so detailed that the validity of the simulation is similar to an experiment. The computational cost is proportional to Re3, thus it is necessary to use a different solution studying turbulent flows at high Reynolds, because the computational resources required by a DNS would exceed the capacity of the most powerful computer currently available. In practical applications, the knowledge of the average quantities is enough to solve the problem of a turbulent flow; the basic idea of the technique RANS (Reynolds Averaged Navier-Stokes Equations) is to derive only the average parameters (mediated in time) from Navier-Stokes equations, reducing the enormous computational cost required by DNS. In practice, the turbulent motion consists of a mean motion and fluctuation over time. Using the decomposition of Reynolds:
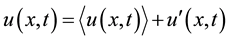 (2)
(2)
where 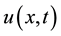 is the instantaneous velocity,
is the instantaneous velocity, 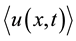 is the average velocity
is the average velocity 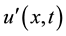 is the speed fluctuating, through Navier-Stokes equations it’s possible to obtain the Reynolds averaged equations. The equations for the mean motion obtained are similar to Navier-Stokes equations with the exception of the divergence of the stress tensor Reynolds: the system resulting from the Navier-Stokes equations is closed, while the system resulting from the RANS simulation is not open because Reynolds tensor introduces 6 additional unknowns. The problem mentioned is known as the problem of closure of turbulence which is solved by introducing models for the turbulent fluctuations which have to reproduce the action of fluctuating terms on mean motion.
is the speed fluctuating, through Navier-Stokes equations it’s possible to obtain the Reynolds averaged equations. The equations for the mean motion obtained are similar to Navier-Stokes equations with the exception of the divergence of the stress tensor Reynolds: the system resulting from the Navier-Stokes equations is closed, while the system resulting from the RANS simulation is not open because Reynolds tensor introduces 6 additional unknowns. The problem mentioned is known as the problem of closure of turbulence which is solved by introducing models for the turbulent fluctuations which have to reproduce the action of fluctuating terms on mean motion.
The K-ε model is one of the most common models of turbulence, even if it is not appropriate in the case of strong adverse pressure gradients. It is a model with two equations: it includes two additional transport equations to represent properties of the turbulent flow and effects such as convection and diffusion of turbulent energy. The first variable transported is the turbulent kinetic energy, k. The second variable transported is the turbulent dissipation, ε; the second variable determines the scale of turbulence, while the first variable k determines the energy in the turbulence. There are two formulations of the K-ε models: the standard k-epsilon model and the RNG k-epsilon model.
In the standard k-epsilon model, eddy viscosity is determined by single length scale turbulence, so the turbulent diffusion is calculated only through a specified scale, whereas in reality all scales of motion will contribute to turbulent diffusion.
The approach RNG (Re-Normalisation Group), a mathematical technique that can be used to obtain a model similar to the k-epsilon turbulence, presents a modified equation ε, which attempts to explain the different scales of turbulence through changes at the term of production of turbulence. The equations used are:
a) Kinematic Eddy Viscosity
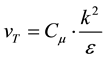 (3)
(3)
b) Turbulence Kinetic Energy
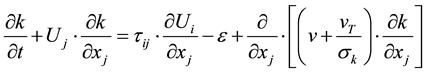 (4)
(4)
c) Dissipation Rate
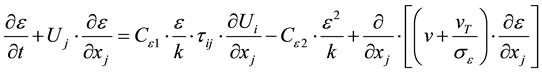 (5)
(5)
Closure coefficient for standard k-epsilon model:
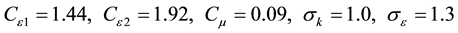
2. Project Description
The purpose of this project is to improve the race performance, reducing the breaking distance and increasing the bending speed. So, we decided to intervene on the drag generated by the wing during the breaking, and also on the grip provided by downforce, function of velocity. To explain the lift, and then the downforce, reference may be made to the wing of an airplane, observing its section. The latter is asymmetric, the top has a profile longer than the bottom: when the wing moves, it separates the relative flow in two parts, so the air layers scroll faster in the top. The outflow over the wing undergoes a boost and then is aerodynamic brake for formula cars accelerated towards the tail at a higher velocity than the air under the wing, which follows a shorter path. So the two currents are reunited in the tail after a same time interval, without creating imbalances. This is not just the facts, but as a first approximation, we can refer to this model. In reference to the Bernoulli trinomial law, since in the lower flow velocity is lower than in the upper, the pressure under the wing has to be greater than that above the wing. Therefore, the difference between the two pressures generates a resultant directed upwards, that is the lift, which holds the aircraft in the air. In detail, lift can be expressed as:
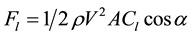 (6)
(6)
where:
・ ρ is the medium density;
・ V is the air velocity;
・ A is the reference surface;
・ Cl is a lift dimensionless coefficient;
・ α is the wing angle of attack.
In racing cars, the wing is mounted upside down and the vertical thrust towards the ground (downforce): this is correlated to the tires grip coefficient. The running resistance depends on its front section, its forward speed, the density of the medium and a drag coefficient. The drag coefficient (Cd) depends on the object shape and size of the object, the medium density and viscosity, the surface roughness, and the object velocity. The aerodynamic resistance (in general fluid dynamics), or drag, is related to a large number of factors, as shown by the formula:
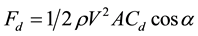 (7)
(7)
where:
• ρ is the medium density of the;
• V is the air velocity;
• A is the reference surface (in case of aircraft is the wing surface, the car front surface);
• Cd is a drag dimensionless coefficient;
• α is the wing angle of attack.
The overall resistance opposed by a fluid medium to the object forward movement is given, in first approximation, by the sum of the frictional resistance, the wake resistance and the induced resistance of lift. In particular, for a tapered body, the flow resistance is given by friction (laminar and/or turbulent), that is the rubbing of the surface against the medium. For this purpose we introduce the concept of boundary layer: it’s the dynamic range, laminar or turbulent, in which internal current speed is subject to strong gradients (continuous changes), due to the viscosity of the fluid. It can be considered as the area that undergoes a disorder, and the velocity is zero on the layer surface (Figure 3).
The thickness of the boundary layer is very small, and it is of one order of magnitude lower than the overall dimensions of the object, that generates the viscose perturbation. Then, inside the boundary layer, the tangential shear stress is “dense”. For this reason in the layer is exerted an intense dissipative braking action, converting part of the movement in thermal agitation. The dissipative action limits the relative velocity between the object and the fluid, which surrounds it. In a turbulent boundary layer, the viscous stresses are added also the stresses, due to the exchange of transverse momentum; these actions increase with the fluid density. The chaos of the turbulent fluid motions implies higher thermal dissipation, so the braking opposing force, in turbulent flow conditions, is greater than that of the laminar regime. The resistance generated, in this way, is affected by the surface roughness: moreover, the rougher surfaces ignite earlier and more easily the turbulent condition in the flow, and then, determine higher resistances. Therefore, it was decided to design some ducts, on the pressure side of the wing, initially covered by special sliding plates, for increasing the aerodynamic drag and downforce [2] .
3. Wing Design
The first phase of the design is to draw the profile of the wing with a CAD software. In this way, it is possible to make a CFD simulation, to evaluate the aerodynamic performance of the wing, in terms of downforce and drag, and estimate the useful angles of attack before stall phenomenon occurs [3] . In fluid dynamics the stall is a reduction of the lift coefficient due to an increase of the angle of attack or due to the incident velocity decrease on an aerodynamic profile, such as an airfoil, a propeller blade or a turbomachinery rotor. The minimum value of the angle of attack for which the stall occurs is called critical angle of attack. This value which corresponds to the maximum lift coefficient, changes significantly, depending on the particular profile or on the considered Reynolds number [4] . Similarly, the profile of the active cavities has been reported, and appropriate simulations were performed. In this way it was possible to estimate the sizes and configurations to achieve the project target. Based on the data collected, the application of these cavities on the wing is studied, evaluating the performance on the different possible arrangements of these cavities. At this moment only 2D simulations have been performed, and a 3D series is considered as future improvement of the project. The models, the different configurations and the results obtained from all the cases mentioned above, will be shown in detail in the following paragraphs.
Geometry Modeling
To approximate the operating conditions of the wing, a control conduit with the dimensions shown in Figure 4(a)
![]()
![]() (a) (b)
(a) (b)
Figure 4. (a) Control conduit; (b) Active cavity dimensions (in mm).
has been chosen. Regarding to the active cavity, the geometry is illustrated in Figure 4(b). The space surrounding the geometry of the aerodynamic and the cavities was discretized using a special dedicated software available as ANSYS package. Furthermore, to observe the progress of the boundary layer, it was built on a reference mesh of 5 layers, with growth factor 1.1, starting from the adjacent profiles of height 0.18 mm (Figure 5). To this purpose, a sizeable set of data was created by means of sufficiently accurate numerical simulations, to derive initial values. The simulations were performed on 3-D models in kinematic similarity using a commercial CFD simulation code, ANSYS/Fluent. The turbulence model was the k-ε realizable, with second order accuracy. Each model was meshed to ensure a y+max ~ 5, a necessary condition for adopting the enhanced wall treatment, since the quality of the grid has a relevant importance on the accuracy and stability of the numerical simulation.
Commercial software allows the “plastering” of cell layers to the critical boundaries of the control volume, which are obviously, in this case, the wall surfaces of the hub, casing and blades. In these zones the usual practice is that of creating a completely structured boundary layer, specifying whenever possible both the height of the first row of cells and the “growth ratio”, i.e. the rate that determines the height of the successive cells. In this process, the height of the first row of cells is usually determined via an empirical formula that gives the value of a wall-based local Reynolds number, denoted by y+ (y+ = u*・y/v where u* = (τwall/ρ)1/2, with τwall being the wall shear stress). For the wing analysis control volume was split in several smaller sub-volumes, to achieve a more consistent set of faces and to better exploit the possibility of creating a locally more refined grid. The choice of the boundary conditions was made as follows: it was performed heuristically, starting from the preliminary sizing data, calibrating them by means of a first simulation, adjusting the values by iteratively resetting the outlet static pressure on the near-wake radial area downstream of the trailing edge. Through subsequent simulations the values of the inlet total pressure and temperature were refined as well in order to ensure conservation of the mass flow rate (the so-called “mass flow inlet condition” was adopted). The turbulent parameters were the turbulence intensity![]() . Rotational periodicity was imposed on all lateral channel surfaces. The number of cells is about 65,000 elements. Finally, the starting boundary conditions are:
. Rotational periodicity was imposed on all lateral channel surfaces. The number of cells is about 65,000 elements. Finally, the starting boundary conditions are:
・ fluid: it is considered air as an ideal gas at constant viscosity;
・ input data: the pressure of 101325 Pa and temperature of 300 K represent the operating conditions.
boundary conditions:
・ inlet → mass flow rate;
・ outlet → pressure outlet;
・ for both, the conditions relating to the model were set on intensity and length scales, with values of 5% and 0.03 m (≃ 1/10 of the rope), respectively;
・ on the upper and lower walls of the duct it has set the periodicity condition;
・ for wing, are set on the condition stationary wall and no slip;
・ for the solution a simple high order term and relaxation has been chosen, by setting for all variables a relaxation factor of 0.25.
4. Simulation Results
4.1. Wing Performance
In this paragraph, the performance of the wing has been analyzed. The results obtained by using CFD simulation (see Figures 6-8), were used as the reference model for the subsequent tests [5] . Since, the following figure shows the results for a 0˚ angle of attack. In particular, for a hypothetical unitary extension wing (1 m), it is obtained:
![]()
![]()
![]()
Figure 6. Pressure, velocity and turbulence plots for 0˚ of angle of attack.
![]()
Figure 7. Plot of Cd and Cdw variation as function of the angle of attack.
![]()
Figure 8. Different cavities configurations. (a) two cavities, (b) two cavities with space increase, (c) see case (b) (d) three cavities.
・ lift coefficient Cl = −0.25762;
・ lift Fl = −312.66 N;
・ drag coefficient Cd = 0.04817;
・ drag Fd = 58.52 N.
Finally, to individuate the stall angle, additional simulations, at different angles of attack, have been performed; precisely 2˚, 4˚, 6˚, 8˚ and 10˚, reporting the values obtained in Table 1. It can be noticed that stall occurs for angles of attack greater than 8˚. The plot of Cd and Cdw is shown in Figure 9.
4.2. Active Cavity Performance Analysis
After some preliminary tests, the dimensions, that characterize the opening and depth of cavities, are 3.5 mm and 3 mm respectively. Later, built a control duct, additional simulation to find the best configuration has been carried out. In particular the configuration used were: two cavities located at 8.22 mm of distance each other, 11.5 mm, 19.72 mm and, finally, three cavities, two equal and one larger radius, interposed to 12.2 mm and 22.74 mm with respect to the remaining two (Figure 8). The analysis have enlightened that the quasi-optimal configuration is the one with the two equal cavities located at intermediate distance: in fact, the last configuration corresponds to the distance limit beyond which the reabsorption of the bubble pressure generated by the cavity in front occurs (circled in red in Figure 9). Based on these considerations, it can proceed to make the cavities on the wing to get the configurations that produce the most desired aerodynamic effects. The trend of fluid velocity is reported in Figure 10.
4.3. Wing with Front Cavities
According to the pressures pattern observed in the case of rear wing with zero angle of attack, in the first instance
![]()
Figure 9. Pressure bubble generated by cavity. In the red circle the reabsorption of the bubble pressure generated by the cavity in front can be seen.
![]()
Table 1. Variation of Cd and Cdw as function of the angle of attack.
![]()
Figure 10. Velocity vectors developed inside the cavity.
it is thought to have a host of ducts on the front half of the wing, because the pressure on that section is lower than the remain aerodynamic one. After that, the CAD geometry has been modified reproducing the chosen configuration, and then we proceeded with the CFD simulation (results in Figure 11). The values obtained confirm the previous considerations:
4.4. Wing with Back Cavities
For comparison, it was decided to realize the same number of cavities in the back half of the wing, leaving smooth the front half area. The CFD simulation results in Figure 12. In particular, it has that:
4.5. Wing with Cavities on the Whole Upper Surface
Finally (see Figure 13), it is decided to extend the group of active cavities over the entire pressure side. The coefficients and the forces derived are:
4.6. Wing with Single Cavity
For evaluating the possible influence of the single cavity on the whole group, further CFD simulations have been carried out and it is placing at different points on the back wing; appropriate pairs combinations have been also considered. Enumerating from 1 to 18 individual ducts starting from closest to the tip of the wing, the results obtained, with these additional series of simulations, are reported in Table 2.
It can be notice that 8 - 9 & 13 - 14 configurations denote an increase in downforce compared to the smooth wing and, at the same time, a decrease in drag.
![]()
![]()
![]()
Figure 11. Pressure, velocity and turbulence plots for wing with front cavities.
![]()
![]()
![]()
Figure 12. Pressure, velocity and turbulence plots for wing with back cavities.
![]()
![]()
![]()
Figure 13. Pressure, velocity and turbulence plots for Wing with cavities on the whole upper surface.
![]()
Table 2. Results of CFD simulations relative to different configuration of cavities over the wing.
5. Simulation Results Analysis
The CFD simulations confirm the theoretical expectations: in particular, three of the above configurations deserve deeper analysis. In detail, it can notice that the wing with active cavities extended to the whole surface and one with the ducts only placed in the tail, show, roughly, the same value of drag (respectively 65.88 N and 61.04 N): however, in the first case, it generates greater downforce (365 N vs N 341). From this observation, it can be inferred that the rear wing with 18 ducts fulfills, in the most effective manner, a better performance, during the braking. While the same wing, but with cavities only located in the back, having a slightly lower drag, could be used during the turns: in fact, referring to the performance of the vehicle, the goal is to have a high grip to deal these turns as quickly as possible. Therefore, the choice of the most efficient set (between the configurations above) depends on the type of curve (more or less fast) and the balance between the drag and downforce forces. So, equipping the wing of pairs 8 - 9 and 13 - 14, for its characteristic to generate more downforce and a lower drag than the smooth aerodynamic profile, it could be used in starting. In fact, in this situation, to have a good sprint, it is desirable to have a low aerodynamic resistance and prevent slipping of the rear wheels: this phenomenon can be achieved by exploiting the downforce generated by the wing in this configuration. The result would be a better grip. Ultimately, you should have a wing that can satisfactory answer the two situations. The configuration must be able to provide an excellent grip and a lower resistance in starting, and get a better behavior in curves. This can be achieved by equipping the wing of sliding panels that open or close the cavities, according to the request of the vehicle.
6. Conclusions and Possible Improvements
The CFD simulations indicate the effectiveness of active cavities, practiced on a formula car rear wing, in order to achieve an aerodynamic brake. Specifically, we can assert that the configuration with the best balance between downforce and drag is that with extended ducts over the entire top surface of the aerodynamic (Fl = −365.172 N, Fd = 65.88 N). Finally, by exploiting the selectivity of sliding panels, as previously explained, it can be realized different wing configurations, depending on the needs required by the race and the sensitivity of the driver.
As regards any improvements, to be made on the performance testing of the brake (the object of study of this paper), more CFD simulations could perform, using a vertical bulkhead on the terminal part of the wing, as well as 3D simulations. In this way, it would be possible to observe the effects of lift drag which should be minimized. Then the next step would be to achieve physically this device, to install it on a formula car and compare experimental data with those obtained by CFD simulations.
Acknowledgements
The research has been partially sponsored by the Italian Government on the framework of Formula Cars/Formula 4 project.
Author Contributions
Roberto Capata and Leone Martellucci contribution dealt with the tests and comparisons, while Enrico Sciubba was in charge of all aspects related to CFD simulations.
Nomenclature Subscripts
A surface [m2] d drag
C coefficient, chord [m] dw downforce
CFD computational fluid dynamic [-] l lift
DRS drag reduction systems [-] ε kinetic dissipation
F force [N] μ viscous
I turbulence intensity [%]
k turbulent kinetic energy [J]
t time [s]
u, U velocity [m/s]
v air speed [m/s]
Greek Symbol
α wing angle of attack [˚]
ε turbolent dissipation [J]
μ dynamic viscosity [kg/m∙s]
ρ density [kg/m3]
τ shear stress [Pa]
ν kinematic viscosity [P]