Valuation of Asian American Option Using a Modified Path Simulation Method ()
1. Introduction
In the recent years, option has become one of well-known financial instruments for hedging strategy. In the financial market, hundreds of options are traded daily. For some cases, options are specifically customized to hedge the market risk of underlying assets and to response market players’ demand. The customized options are developed based on the characteristics of underlying assets. For example, the famous Black-Scholes model is relied on assumption that the underlying asset price dynamic follows the Geometric Brownian motion (GBM). It means that the log return of asset is normally distributed. This model is widely used to determine the price of European and American options.
However, many research in modeling the asset price dynamics found that the distribution of the log return of asset price mostly has the excess kurtosis and leptokurtic distribution. This fact shows that the GBM model fails to describe the behavior of the asset price dynamics, and therefore, the log return of the asset price is not suitable to be modeled by a normal distribution. In Indonesia market, the dynamics of some stock indices such as Jakarta Composite Index (JCI) and Jakarta Islamic Index (JII), confirm this situation. In order to overcome this situation, the Variance Gamma (VG) process, a class of Levy process, has been developed and it can capture those excess kurtosis and leptokurtic distribution [1]. Valuation of European and American options where the dynamics of the assets prices follow the VG process can be found in [2]. However, in general, modelling dynamics of financial instruments under the VG process has not been widely well developed and only a few literature available on it. Madan and Seneta [3] have proposed a closed form formulae to determine the price of an European option. In general, finding the existing model to valuation path-dependent options under the VG process is still a challenging task.
The contribution of this paper is to determine the price of Asian option using VG model and compare option prices between an Asian European and Asian American option according to some performance criteria. We also develop a new approach by using the conditional distribution of the VG process to determine the price of Asian European options. To price Asian American options, we apply the modified path simulation method based on Tiley [4] which is similar to valuation of American options. In deriving the method, Tiley [4] assumed that the underlying asset price dynamics follow the GBM. Performance of the modified path simulation method applied to Asian American options is investigated by comparing the obtained Asian American option prices to the Asian European option prices. Comparison in terms of option prices is also provided with the plain vanilla European option and plain vanilla American option.
The organization the rest of this paper is as follows. In Section 2, we describe Asian option, while the modi- fied path simulation method for Asian American option is given in Section 3. Simulation study is given in Section 4 and in the last section we give conclusions and further research.
2. Asian Option
Asian option is an option whose payoff depends on the arithmetic average price of underlying asset over a certain period of time, from the initiation of the contract until its maturity date. It is assumed that the underlying asset price dynamics follow the VG process, under the risk-neutral process. By considering the discrete avera-
ging times: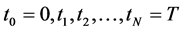 , where
, where 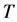 is the time to maturity, the underlying asset price at time
is the time to maturity, the underlying asset price at time , denoted by
, denoted by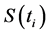 , is given as follows
, is given as follows
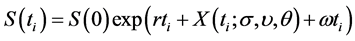
The arithmetic average price of underlying asset at time , denoted by
, denoted by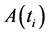 , is defined as:
, is defined as:
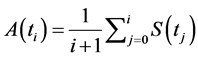
where  The payoff of European Asian option with the strike price
The payoff of European Asian option with the strike price  is given by:
is given by:

 .
.
The existing methods to determine the price of a European option, (see for example Madan and Milne [5]) cannot be directly applied for Asian option. The reason is the arithmetic average of variables following the VG process does not follow the VG process. The easiest way to value the Asian European option is to apply the Monte Carlo simulation. First, we generate a finite sample of 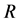 underlying asset paths whereeach path has
underlying asset paths whereeach path has 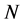 epochs. It is assumed that the k-th path in the sample is represented by the sequence:
epochs. It is assumed that the k-th path in the sample is represented by the sequence:  . Namely
. Namely  is
is  at the k-path. For the k-th path we will have the sequence of the Arithmetic average prive:
at the k-path. For the k-th path we will have the sequence of the Arithmetic average prive:
![]()
where![]() . By using that path, we can value the European Asian call and put options as follows:
. By using that path, we can value the European Asian call and put options as follows:
![]()
![]() .
.
Valuation of American Asian option under the VG process is more difficult than the European Asian option since the characterization of the American option is more complex than the European one. And also, the Monte Carlo simulation method cannot be directly applied in valuing the American Asian option. We will adopt and modify that approach to determine the price of American option under the VG process assumption.
3. Modified Path Simulation Method for Asian American Option
One approach to determine the price of the American option is using simulation. However, many literatures found that simulation such as Monte Carlo simulation, cannot determine the price of the American option efficiently (see Dyer and Jacob [6], Geske and Shastri [7], Tiley [8]). Simulation requires large amounts of compu- ter processing time and execution time. Based on this fact, Tiley [4] has developed an algorithm so-called the path simulation model to value the American option more efficiently. In the algorithm, free-arbitrage underlying asset prices are sampled, and the option price is estimated based on these sample paths. In this paper, that approach will be adopted to determine the American option price under the VG process assumption. We call this approach as a modified path simulation method. The procedure for valuing American option using this method can also be found in section 2.3 of [2].
The first step of the algorithm is to generate a finite sample of ![]() underlying asset paths, where each path has
underlying asset paths, where each path has ![]() epochs (see Avramidis, L’Ecuyer, P. and Tremblay [9]). It is assumed that the k-th path in the sample is
epochs (see Avramidis, L’Ecuyer, P. and Tremblay [9]). It is assumed that the k-th path in the sample is
represented by the sequence:![]() . For the k-th path we will have the sequence of the arithmetic average price:
. For the k-th path we will have the sequence of the arithmetic average price:![]() , where
, where![]() . The
. The
next step is to reorder the arithmetic asset price paths from the highest to the lowest for an Asian call option or from the lowest to the highest for an Asian put option. We then make partition for the set of ![]() paths into
paths into ![]() distinct bundles of
distinct bundles of ![]() paths each.
paths each.
Let be defined the intrinsic value ![]() of the option on path
of the option on path ![]() at epoch
at epoch ![]()
![]() as:
as:
![]()
The holding value ![]() is the expectation current value option over all paths in the bundle containing the path-k. Holding values are equal in the same bundles. The core of this algorithm is in determining the path index
is the expectation current value option over all paths in the bundle containing the path-k. Holding values are equal in the same bundles. The core of this algorithm is in determining the path index
![]() as the sharp boundary to decide whether to hold or to exercise the option. The exercise-or-hold variable
as the sharp boundary to decide whether to hold or to exercise the option. The exercise-or-hold variable ![]() is assume to be 1 for
is assume to be 1 for![]() , and 0 for
, and 0 for![]() . The indicator variable
. The indicator variable ![]() is defined as follows
is defined as follows
![]()
The current option value equals to intrinsic value when the option is exercised, and equals to holding value when the option is hold. Using backward induction, we can estimate the option price at time 0. However in this algorithm, the accuracy of this estimation depends on partition of the paths we chose.
4. Simulation Study
In this section, several scenarios are considered in comparing the option prices for Plain Vanilla European option, Plain Vanilla American option, Asian European option and Asian American option. Option prices for the Plain Vanilla European option and Asian European option were determined through Monte Carlo simulation, modified path simulation method was employed to determine option prices for the Plain Vanilla American option and Asian American option. In all of those methods, the parameters we use came from the VG process. In all the scenarios below, we use the value of S(0) = 100 K = 100, T = 1 year and r = 5%/year. The results are given in the table below.
From Table 1, we can conclude that American options always more expensive than European options, both for plain vanilla and Asian type. This finding is in line with what we have in theory, since American options can be exercise any time before their maturity, while European options can only be exercised at maturity date. In real world, American options are traded more frequently than European options. Asian options are also cheaper than plain vanilla options due to averaging the asset prices in calculating payoff of Asian options. Averaging the asset prices will damp or reduce the volatility and this will make option prices cheaper of the Asian type compared to the plain vanilla type.
Comparing the results of Scenario 1 vs. Scenario 2 and Scenario 3 vs. Scenario 4, it can be concluded that when volatility (σ) becomes larger, the option prices become more expensive. This is reasonable as volatility is
![]()
Table 1. Option prices for different scenarios.
related to risks. Higher volatility implies higher risks for asset holder. Hedging using option for riskier asset becomes more expensive. In comparing Plain Vanilla option prices to Asian option prices, it can be concluded that the higher the volatility the more discrepancy in their prices. This finding is inline with the usage of Asian option as hedging instrument for the underlying asset prices. Using Plain Vanilla option as a hedging instrument will incure higher cost if the volatility of the underlying asset prices is also higher.
On the other hand, if we compare results of Scenario 1 vs. Scenario 3 and Scenario 2 vs. Scenario 4, higher kurtosis will cause cheaer option prices, since higher kurtosis (with the same mean, deviation standard and skewness) will make log return of the asset prices tend to their mean, and the risk becomes smaller. This is quite make sense as in asset price or option price modelling, people tends to use its mean.
The above conclusions are strengthen by simulation results for Asian European option prices as depicted in Figures 1-3. Figure 1 shows Asian European option prices for several values of volatility and skewness. In Figure 2, Asian European option prices for different values of kurtosis dan skewness are presented, while Figure 3 gives Asian European option prices for various values of kurtosis and volatility. We can conclude that from these three figures, option prices are indeed affected by skewness, volatility and kurtosis of the log return under- lying asset. The higher the volatility the more expensive the call option prices. The further the value of skewness from zero, the more expensive the option prices and the higher the kurtosis the cheaper the call option prices. In general, the results found in Table 1 and Figures 1-3 are reasonable and in line with characteristics of the options themselves, and indeed the method of path simulation performs well in valuation of the option prices.
5. Conclusion and Further Research
We propose a modified path simulation model to value an Asian American option under VG process. Several scenarios have been investigated, especially by comparing Asian American option prices with Plain Vanilla and Asian European option prices. It was found that the proposed method gives option prices that inline with the characterization of each option type. Some scenarios have also been developed to confirm the option prices obtained using the modified path simulation method for different values of parameters. In general, we can conclude that the proposed method performs quite well and can be used as an alternative for determining the option prices, especially for Asian American options.
For further research, we would also like perform sensitivity analysis of the proposed method in determining option prices for both European and American options, using real data in Indonesia market. We want to compare the option prices and Value-at-Risk (VaR) calculation obtained by the proposed method to those obtained by Black-Scholes.
![]()
Figure 1. Asian European call option process for different values of volatility and skewness.
![]()
Figure 2. Asian European call option process for different values of kurtosis and skewness.
![]()
Figure 3. Asian European call option process for different values of volatility and kurtosis.
Acknowledgements
Funding of this research from the Directorate of Research and Community Services, Indonesian Directorate General of Higher Education (DP2M-DIKTI) under the Research Grant Competition 2014-2016 scheme is highly acknowledged.