The Best Constant of Discrete Sobolev Inequality on a Weighted Truncated Tetrahedron

Yoshikatsu Sasaki

Department of Mathematics, Hiroshima University, Higashi-Hiroshima, Japan.

DOI: 10.4236/wjet.2015.33C022                

Abstract

The best constant of discrete Sobolev inequality on the truncated tetrahedron with a weight which describes 2 kinds of spring constants or bond distances. Main results coincides with the ones of known results by Kametaka et al. under the assumption of uniformity of the spring constants. Since the buckyball fullerene C60 has 2 kinds of edges, destruction of uniformity makes us proceed the application to the chemistry of fullerenes.

Keywords

The Best Constant, Sobolev Inequality, Discrete Laplacian, Weighted Graph, Truncated Polyhedron

1. Introduction

Sobolev inequality known as Sobolev embedding theorem plays an important role in the theory of PDEs. Brezis [1, Chap.IX] gave some constant of Sobolev inequality, and mentioned that the best constant was known and complex. Talenti [2] and Marti [3] studied the best constant by use of variational methods.

Kametaka and his coworkers studied the best constant of Sobolev inequality in view of the boundary value problem [4]-[8], and then they studied discrete Sobolev inequality [9]-[13] aiming to application to the C60 buckyball fullerene [14]. Table 1 is a summary of Kametaka school; in this table, Rn stands for the regular n-hedron, and Tn stands for the truncated n-hedron. In classical geometry, each truncated n-hedra is known as a member of Archimedean polyhedra. Note that the works of Kametaka school on each polyhedron is under the assumption of uniformity of the spring constants.

On the other hand, in chemistry of fullerenes [15], the structure of the fullerenes is studied in detail. [16]-[18] tell us that the bond lengths of the C60 buckyball fullerene are of 2 kinds. So, in prospects for application to the chemistry of fullerenes, the assumption of uniformity of the spring constants should be thrown away.

This article concerns with the best constant of discrete Sobolev inequality on T4 with 2 kinds of spring constants, in other words, a weighted T4 graph. The results of Kametaka school for R4 [10] and T4 [12] are generalized in the next section. The outline of this article follows the paper of Kametaka school on Rn [10].

2. Discrete Laplacian and Discrete Sobolev Inequality

2.1. Main Results

Consider the truncated tetrahedron T4. It has 12 vertices, and let us number the vertices 0, 1, …, 11 as in Figure 1, similar to [12]. Put

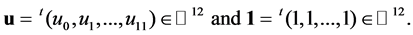
Define the bond matrix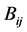, as in Figure 2, by

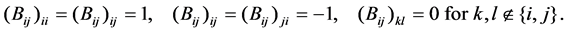
Note that Let us represent each edge of T4 by the couple of the numbers of both vertices, identifying with. Put

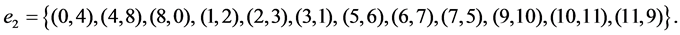
is the set of original edges of R4, and is the set of edges of T4 created by the truncation. Let us denote the ratio of the spring constant of each egde of to one of each edge of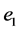, and introduce 2 kinds of the Sobolev energies as follows:

Here, 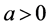is a dumping parameter. Define the weighted discrete Laplacian

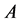is also represented as follows:

Figure 1. Numbering of the vertices of T4.

Figure 2. Bond matrix.

By use of the weighted Laplacian defined as above, the Sobolev energies are written as follows:

The eigenvalues of are as follows:

where. Let us stand for the eigenvalues of. Note that 0 is a simple eigenvalue of with the corresponding eigenvector, and is the projection matrix to the eigenspace corresponding to the eigenvalue 0. Let us introduce the Green matrix of by

For the Green matrix, there exists a unique matrix satisfying

is the Penrose-Moore genelarized inverse matrix of, and is called the pseudo green matrix of. We see that

Theorem 1. There exists a positive constant independent of such that, for every satisfying, the discrete Sobolev inequality

holds. Among such, the best constant is

Theorem 2. There exists a positive constant independent of such that, for every, the discrete Sobolev inequality

holds. Among such, the best constant is

Remark. in Theorem 1 coinsides with for which appears in [12] for T4, and with for, which appears in [10] for R4. So, the main result covers the results by Kametaka school (cf. Table 1).

(a) (b)

Table 1. The best constants on polyhedra known by Kametaka school. (a) Regular n-hedron (=Rn) [10]; (b) Truncated n-he- dron (=Tn) [9] [12].

2.2. Proof

Let be the normalized eigenvectors of, i.e. where is the Kronecker’s delta. is unitary. Let Put. We have

Note that Then,

Definition. For any, we define

Lemma. For every, we have the reproducing equality as follows:

Remark. So, is the reproducing kernel on.

Proof of Lemma. Since and, we have

Proof of Theorems. Applying the Schwarz inequality to the reproducing equality, we have

Using we have

Then we obtain discrete Sobolev inequality:

Then, for

Combining it with the trivial inequality

We obtain the conclusion of Theorem 1. Theorem 2 is similarly proved.

3. Discussion and Prospects

Kametaka school says that the high symmetry of Rn or Tn allows us to compute the exact expression of the best constant. However, the introduction of our weight does not destroy the computability of this problem because our weighted Laplacian is still symmetric matrix. Whether our model with weight is appropriate or not is another problem. It depends on what kind of problem we want to apply our model to.

And, after this article, the author wish to study the Tn for n = 6, 8, 12, 20, and application to the interaction of fullerene and another molecules. The high symmetry move us to its beauty however, the destruction of the symmetry also fascinates us.

Acknowledgements

The author thanks Prof. T. Masuda for his suggestion to read one of the papers of Kametaka school on the best constant of discrete Sobolev inequality, and also thanks his friends S. Fuchigami, R. Inoue and S. Minami for helpful discussion.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Brezis, H. (1983) Analyse fonctionnelle: Théorie et applications. Masson, Paris.
[2]	Talenti, G. (1976) The Best Constant of Sobolev Inequality. Annali di Matematica Pura ed Applicata, 110, 353-372. http://dx.doi.org/10.1007/BF02418013
[3]	Marti, J.T. (1983) Evaluation of the Least Constant in Sobolev’s In-equality for . SIAM J. Numer. Anal., 20, 1239-1242. http://dx.doi.org/10.1137/0720094
[4]	Kametaka, Y., Yamagishi, H., Watanabe, K., Nagai, A. and Takemura, K. (2007) Riemann Zeta Function, Bernoulli Polynomials and the Best Constant of Sobolev Inequality. Sci. Math. Japan, 65, 333-359.
[5]	Kametaka, Y., Watanabe, K. and Nagai, A. (2005) The Best Constant of Sobolev Inequality in an n Dimensional Euclidean Space. Proc. Japan Acad., Ser. A, 81, 57-60. http://dx.doi.org/10.3792/pjaa.81.57
[6]	Kametaka, Y., Watanabe, K., Nagai, A. and Pyatkov, S. (2005) The Best Constant of Sobolev Inequality in an n Dimensional Euclidean Space. Sci. Math. Japan, 61, 15-23.
[7]	Yamagishi, H., Kametaka, Y., Nagai, A., Watanabe, K. and Takemura, K. (2009) Riemann Zeta Function and the Best Constants of Five Series of Sobolev Inequalities. RIMS K?ky?roku Bessatsu, B13, 125-139.
[8]	Yamagishi, H., Kametaka, Y., Takemura, K., Watanabe, K. and Nagai, A. (2009) The Best Constant of Discrete Sobolev Inequality Corresponding to a Bending Problem of a Beam under Tension on an Elastic Foundation. Trans. Japan Soc. Ind. Appl. Math., 19, 489-518. (In Japanese)
[9]	Kametaka, Y., Nagai, A., Yamagishi, H., Takemura, K. and Watanabe, K. (2014) The best constant of Dicrete Sobolev Inequality on the C60 Fullerene Buckyball. arXiv.org e-Print Archive. http://arxiv.org/abs/1412.1236
[10]	Kametaka, Y., Watanabe, K., Yamagishi, H., Nagai, A. and Takemura, K. (2011) The Best Constant of Discrete Sobolev Inequality on Regular Polyhedron. Trans. Japan Soc. Ind. Appl. Math., 21, 289-308. (In Japanese)
[11]	Nagai, A., Kametaka, Y., Yamagishi, H., Takemura, K. and Watanabe, K. (2008) Discrete Bernoulli polynomials and the Best Constant of Dicrete Sobolev Inequality. Funkcial. Ekvac., 51, 307-327. http://dx.doi.org/10.1619/fesi.51.307
[12]	Yamagishi, H., Kametaka, Y., Nagai, A., Watanabe, K. and Takemura, K. (2014) The Best Constant of Dicrete Sobolev Inequality on Truncated Polyhedra. Abstract of the 10th Meeting of the Union of Research Activity Groups, Japan SIAM, Kyoto Univ., Kyoto, 9-10 March 2014. (In Japanese) http://chaosken.amp.i.kyoto-u.ac.jp/_src/sc2490/jsiam_s2_no4_yamagisi_abst.pdf
[13]	Yamagishi, H., Kametaka, Y., Nagai, A., Watanabe, K. and Takemura, K. (2013) The Best Constant of Three Kinds of Dicrete Sobolev Inequalities on Regular Polyhedron. Tokyo J. Math., 36, 253-268. http://dx.doi.org/10.3836/tjm/1374497523
[14]	Kroto, H.W., Heath, J.R., O’Brien, S.C., Curl, R.F. and Smalley, R.E. (1985) C60: Buckminsterfullerene. Nature, 318, 162-163. http://dx.doi.org/10.1038/318162a0
[15]	Shinohara, H. and Saito, Y. (2011) Science of fullerenes and CNTs. Nagoya University Press, Nagoya.
[16]	Hawkins, J.M., Meyer, A.L., Timothy, A., Loren, S. and Hollander, F.J. (1991) Scinence 252, 312. http://dx.doi.org/10.1126/science.252.5003.312
[17]	Hedberg, K., et al. (1991) Bond Lengths in Free Molecules of Buckminsterfullerene, C60, from Gas-Phase Electron Diffraction. Science, 254, 410. http://dx.doi.org/10.1126/science.254.5030.410
[18]	Yannoni, C.S., Bernier, P.P., Bethune, D.S., Meijer, G. and Sa-lem, J.R. (1991) NMR determination of the bond lengths in C60. J. Am. Chem. Soc., 113, 3190-3192. http://dx.doi.org/10.1021/ja00008a068