New Modification of Fixed Point Iterative Method for Solving Nonlinear Equations ()
1. Introduction
In recent much attention has been given to establish new higher order iteration schemes for solving nonlinear equations. Many iteration schemes have been established by using Taylor series, Adomain decomposition, Homotopy pertrubation technique and other decomposition techniques [1] -[6] . We shall modify the fixed point method using taylor series on the functional equation 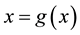 of nonlinear equation
of nonlinear equation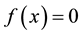 . Initially, we do not put any restrictions on the original function f. In fixed point method, we rewrite
. Initially, we do not put any restrictions on the original function f. In fixed point method, we rewrite 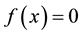 as
as 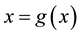 where
where
1) There exist 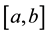 such that
such that 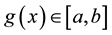 for all
for all 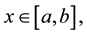
2) There exist  such that
such that 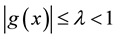 for all
for all 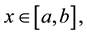
The order of convergence of a sequence of approximation is defined as:
Definition 1.1 [7] Let the sequence 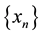 converges to
converges to . If there is a positive integer p and real number C such that
. If there is a positive integer p and real number C such that
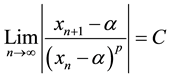
then p is order of convergence.
Theorem 1.2 (see [6] ). Suppose that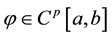 . If
. If , for
, for 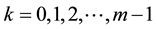 and
and ![]() , then the sequence
, then the sequence ![]() is of order m.
is of order m.
2. New Iteration Scheme
Consider the nonlinear equation
![]() (2.1)
(2.1)
we can rewrite the above equation as
![]() (2.2)
(2.2)
We suppose that ![]() is a root of (2.1) and
is a root of (2.1) and ![]() is initial guess close to
is initial guess close to![]() . We can rewrite Equation (2.2) by using Taylor’s expansion as:
. We can rewrite Equation (2.2) by using Taylor’s expansion as:
![]() (2.3)
(2.3)
if we truncate Equation (2.3) after second term then, we obtained
![]()
From above formulation we suggest the following algorithm for solving nonlinear Equation (2.1).
In algorithem form, we can write
![]()
we approximate
![]()
Thus
![]()
if we take
![]()
then we have the following algorithem;
Algorithm 2.1 For a given![]() , we approximation solution
, we approximation solution ![]() by the iteration scheme:
by the iteration scheme:
![]()
If we truncate Equation (2.3) after third term then we have
![]()
![]()
![]()
![]()
In algorithem form, we can write
![]()
we approximate
![]()
By substituting in above, we have
![]()
Thus, we have the following algorithem;
Algorithm 2.2 For a given![]() , we approximation solution
, we approximation solution ![]() by the iteration scheme:
by the iteration scheme:
![]()
3. Convegence Analysis
In this section, we discuss the convergence of Algorithm (2.1) and (2.2).
Theorem 3.1 Let ![]() for an open interval I and consider that the nonlinear equation
for an open interval I and consider that the nonlinear equation ![]() (or
(or![]() ) has simple root
) has simple root![]() , where
, where ![]() be sufficiently smooth in the neighbourhood of the root
be sufficiently smooth in the neighbourhood of the root![]() . If
. If ![]() is sufficiently close to
is sufficiently close to ![]() then iteration scheme defined by Algorithm 2.1 has at least second order convergence.
then iteration scheme defined by Algorithm 2.1 has at least second order convergence.
Proof. Let ![]() be simple zero of
be simple zero of ![]() and
and ![]() be its functional equation. Let
be its functional equation. Let ![]() and
and ![]() be errors at nth and (n + 1)th iterations respectively. Then expanding
be errors at nth and (n + 1)th iterations respectively. Then expanding ![]() and
and ![]() about
about![]() , we have
, we have
![]() (3.1)
(3.1)
and
![]() (3.2)
(3.2)
Algorithem (2.1) is given by
![]()
By substituting values from Equations (3.1) and (3.2) in above, we get
![]()
![]()
Hence algorithem (2.1) has second order convergence.
Theorem 3.2 Let ![]() for an open interval I and consider that the nonlinear equation
for an open interval I and consider that the nonlinear equation ![]() (or
(or![]() ) has simple root
) has simple root![]() , where
, where ![]() be sufficiently smooth in the neighbourhood of the root
be sufficiently smooth in the neighbourhood of the root![]() . If
. If ![]() is sufficiently close to
is sufficiently close to ![]() then iteration scheme defined by Algorithm 2.2 has at least third order convergence.
then iteration scheme defined by Algorithm 2.2 has at least third order convergence.
Proof. Let ![]() be simple zero of
be simple zero of ![]() and
and ![]() be its functional equation. Let
be its functional equation. Let ![]() and
and ![]() be errors at
be errors at ![]() and
and ![]() iterations respectively. Then expanding
iterations respectively. Then expanding![]() ,
, ![]() and
and ![]() about
about![]() , we have
, we have
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
Algorithem (2.2) is given by
![]()
By substituting values from Equations (3.3), (3.4) and (3.5) in above, we get
![]()
![]()
Hence the order of convergence fo algorithm 2.2 is least 3.
4. Numerical Results
In this section, we present some example to make the comparitive study of fixed point method (FPM), Newton method (NM), Abbasbandy method (AM), Homeier method (HM), Chun method (CM), Householder method (HHM), Algorithem 2.1 and Algorithm 2.2 developed in this paper. We use![]() . The following criterias are used for computer programs:
. The following criterias are used for computer programs:
1) ![]()
2) ![]()
We consider the following examples to illustarate the performance of our newly established iteration scheme.
![]()
![]()
![]()
![]()
![]()
![]()
Comparison Table
5. Conclusion
We have modified the fixed point method for solving nonlinear equations. We have established two new algorithems of convergence order two and three. We have solved some nonlinear equations to show the performance and efficiency of our newly developed iteration schemes. From comparison table, we conclude that these schemes perform much better than Newton method, Abbasbandy method, Chun method, Homeier method, Householder method etc.