Pricing American Options Using Transition Probabilities: A Dynamical Systems Approach ()
1. Introduction
There are several methods for pricing European and American options [1] - [17] . We are interested in different ways to price American options that are flexible enough, so that they can be useful in nonstandard situations, or offer alternatives in standard settings.
Our main goal is to present a new way to price American options, which allows us to introduce the effect of macroeconomic factors that affect the financial market so we can introduce different dynamics for the under- laying asset and generalize more complex processes such as Levy processes.
This new formula does not pretend to improve on the existent methods in the context of the Black-Scholes model. We want to show that it is consistent with it. In fact it is equivalent to a previous one given by Carr, Jarrow and Minery [5] . The most interesting feature of this method is that it explicitly introduces the transition probability as a solution to a Fokker-Planck (Kolmogorov) equation. This allows us to consider more general situations when the underlaying asset does not follow a log-normal process.
We propose an extension of Samuelson’s formula for American type contingent claims, because one of the most interesting aspects of this formula is that it does not make explicit reference to the risk neutral distribution, but the physical or observed one (see Section 2 below).
For the fixed underlaying asset value S we propose that the American option price is:
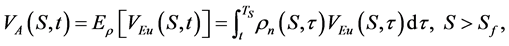 (1)
(1)
where for each time 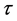 of S,
of S, 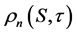 is the normalized solution of the corresponding Fokker-Planck equa- tion (for the probability density function),
is the normalized solution of the corresponding Fokker-Planck equa- tion (for the probability density function), 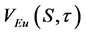 is the solution of the Black-Scholes equation for the Euro- pean case,
is the solution of the Black-Scholes equation for the Euro- pean case,  is the free boundary and
is the free boundary and 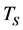 corresponds to the expiration time at the free boundary, which de- pends on the location of the free boundary (for details see section 3).
corresponds to the expiration time at the free boundary, which de- pends on the location of the free boundary (for details see section 3).
For practical purposes, we present a theoretical example introducing the effect of macroeconomic factors in a derivative model, and for consistency, we prove that this formula satisfies the Black-Scholes inequality for American options in the log-normal case.
In what follows we define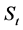 : The underlaying asset price at time t. E: Exercise price or maturity price. T: Exercise time or maturity time.
: The underlaying asset price at time t. E: Exercise price or maturity price. T: Exercise time or maturity time.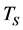 : Time to early exercise (on the free boundary). t: Current time. r: Free risk interest rate.
: Time to early exercise (on the free boundary). t: Current time. r: Free risk interest rate.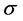 : Underlaying asset volatility.
: Underlaying asset volatility.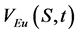 : European option price.
: European option price.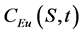 : European call option price.
: European call option price.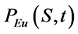 : European put option price.
: European put option price. : American put option price.
: American put option price.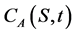 : American call option price.
: American call option price.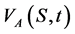 : American option price.
: American option price.
To value European type options there are explicit and standard formulas as Black-Scholes formula [14] , Samuelson formula [18] , an actuarial approach [2] , Merton’s theory of rational option pricing [9] , etc. However, to value an American options there are not closed formulas. Nowadays, there are several representations to approximate the value of American options. In general, there are not closed expressions except in special situations. In the case that a formula exists, it can be very complex. The best way to price American options in practice is to use numerical methods (explicit, implicit, finite differences, between others) although they can be complicated, too.
The options are typically used for development of structural products, speculation strategies and hedging. Most of the options traded in the international markets are of American type.
For consistency, our objective is to prove analytically that (1) also coincides with standard approach in the literature as the Black-Scholes formula. We also compare its numerical implementation with the existent numerical methods such as: binomial trees, explicit and implicit partial differential equations methods.
In (1), we assume that we know a priori the location (or some approximation) of the free boundary. Existing methodologies both analytical and numerical can be used to approximate well the free boundary.
This article is structured in the following way. In the second section, we describe the Kolmogorov equations, which represents the transition probability density function in (1). In the third section, we present the formula to price the American options, as well as, some numerical examples and compare with others numerical methods. Finally, we give some conclusions and open problems.
2. Preliminaries
To understand the mechanism of our approach, we are going to describe the Kolmogorov backwards equation and Kolmogorov forward equation (Fokker-Planck equation). They are important tools for finding the pro- bability density function.
The Transition Probability Density Function
We derive an equation for the probability density function of a random variable defined by a stochastic differential equation (SDE). This density describes the temporal evolution of the state, x, of the phenomenon under study.
We introduce a general random variable x, which satisfies the SDE:
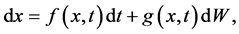 (2)
(2)
where f and g are any continuously differentiable functions of x and t, and W is the Wiener process or Brownian motion.
Then, the transition probability density function is denoted by ![]() with
with![]() ,
, ![]() and
and ![]() the future values of x and t respectively.
the future values of x and t respectively.
It is well know that p satisfies:
![]() (3)
(3)
with the initial condition
![]()
where ![]() is the Dirac delta function.
is the Dirac delta function.
Conversely, if we know the value ![]() at time
at time![]() , then we can determine an equation for the probability density function for x at an earlier time t. This is called the backwards Kolmogorov equation and it is given by
, then we can determine an equation for the probability density function for x at an earlier time t. This is called the backwards Kolmogorov equation and it is given by
![]() (4)
(4)
with final condition given by
![]()
For a detailed presentation of these subjects see [14] [19] - [22] .
3. Alternative Formula to Estimate American Options
We are going to evaluate an American option applying Samuelson’s formula ( [2] [18] ), using the transition probability density to generate the function corresponding to the physical measure as the solution of a Fokker- Planck type equation ( [19] [20] [23] - [25] ). For consistency, we are going to prove this new formula recovers the traditional Black-Scholes results in the log-normal case ( [10] [12] [14] [23] [26] - [28] ) for the price of an American put option. We are also going to compare this proposal with specific examples estimated with the tree methods (Cox, Ingersoll and Rubinstein) and the finite differences, explicit and implicit methods.
The main idea behind this formulation is that we can use the Fokker-Planck equation in more general or complex problems in order to incorporate the effect of macroeconomic factors to several models of financial derivatives and credit risk, where we do not know a priori the real distribution of the density and where the underlying asset does not follow a log-normal distribution.
3.1. A General Formula for Models Incorporating Macroeconomic Variables
The importance of considering macroeconomic factors in pricing standard or credit risk derivatives is that they considerably affect their value (see [29] ).
Our idea is to extend this model to the case where the parameters may depend directly on different macroeconomic factors or indices. In order to do this we generate the probability density function through the Fokker-Planck equation, which will allow us to systematically introduce the effect of macroeconomic factors on the option-pricing model.
We have a financial model that takes into account the effect of macroeconomic factors. Suppose we want to calculate the financial derivative value with underlying asset S, but the parameters ![]() and
and ![]() are dependent on n macroeconomic factors.
are dependent on n macroeconomic factors.
We consider that a macroeconomic environment is formed by n variables,
![]() , which are represented by the dynamics:
, which are represented by the dynamics:
![]() (5)
(5)
![]()
where ![]() is a function that depends on macroeconomic factors and time,
is a function that depends on macroeconomic factors and time, ![]() is a constant and
is a constant and ![]() repre- sents a Brownian motion1.
repre- sents a Brownian motion1.
Now, we suppose that the underlying asset, in general, is governed by the stochastic differential equation:
![]() (6)
(6)
In this case, the way to introduce the macroeconomic factors and time is through the return rate![]() , the volatility
, the volatility ![]() and the free risk interest risk r. In this step it is necessary to calibrate the model in such a way as to determine the effect that such factors have on the parameters.
and the free risk interest risk r. In this step it is necessary to calibrate the model in such a way as to determine the effect that such factors have on the parameters.
On the other hand, we calculate the transition probability through the Fokker-Planck equation, but generalized to n variables2. In this case, ![]() is the probability of finding the system in state X at time t.
is the probability of finding the system in state X at time t.
The advantage of using this equation lies in being able to represent concisely the dynamics of the system of equations by a single partial differential equation, via the transition probability function.
Finally, we can apply Samuelson formula or our formula to obtain the price of American or European options:
![]() (7)
(7)
With ![]() the underlying asset price,
the underlying asset price, ![]() is the early exercise time on the free boundary.
is the early exercise time on the free boundary.
The Fokker-Planck equation can be used in credit risk and present net value problems (see [30] ), among many other cases where the transition probability follows more general processes, such as Lévy process.
We will consider the case of an American option on a single underlying asset following a log-normal process. Here ![]() and
and ![]() are constant.
are constant.
3.2. Alternative Formula for Pricing American Options
Introducing the alternative formula for estimating American options, we define the American option price with- out dividends in the following way. For a fixed S, we have:
![]() (8)
(8)
with
![]()
where![]() ,
, ![]() is the free boundary,
is the free boundary, ![]() is current time,
is current time, ![]() is the early exercise time on the free boundary3, T is the maturity time (to see the relation between the times T and
is the early exercise time on the free boundary3, T is the maturity time (to see the relation between the times T and ![]() see Figure 1),
see Figure 1), ![]() is the normalized probability that the asset takes the value S at time t and
is the normalized probability that the asset takes the value S at time t and ![]() is the analytical solution to the Black-Scholes equation , namely:
is the analytical solution to the Black-Scholes equation , namely:
![]()
Figure 1. Relationship between the times T and TS.
![]() (9)
(9)
where
![]()
![]()
and ![]() is the cumulative normal distribution function with zero mean and standard deviation equal to one.
is the cumulative normal distribution function with zero mean and standard deviation equal to one.
The consistency conditions are:
![]() (10)
(10)
and
![]() (11)
(11)
There is another alternative formula to estimate American options where the integration is with respect to time too (see [5] ).
Before proceeding with the details of our alternative formula it is necessary to define the location of the free boundary. We present the results we need in the following section.
Free Boundary
The problem of finding the American option value translates into finding a solution to a free boundary problem. The strategy for approaching the solution is to locate the free boundary,![]() .
.
So if ![]() is continuous and monotone, there exists a value
is continuous and monotone, there exists a value![]() , where the free boundary is located and
, where the free boundary is located and ![]() for a put option and
for a put option and ![]() for a call option.
for a call option.
For a Call option (CA):
![]() (12)
(12)
Put option (PA):
![]() (13)
(13)
The curve ![]() divides the plane
divides the plane ![]() in two parts as shown in Figure 2. The shaded parts of both graphs, represent the domain where the option, call
in two parts as shown in Figure 2. The shaded parts of both graphs, represent the domain where the option, call ![]() or put
or put![]() , is not exercised and its value is given by:
, is not exercised and its value is given by:
![]()
Figure 2. Region of solution of an American option.
![]() (14)
(14)
The region outside the curve, ![]() , is where the option is exercised. This region for the call option is
, is where the option is exercised. This region for the call option is ![]() and for the put option is
and for the put option is![]() , and its value is given by their respective payoff function,
, and its value is given by their respective payoff function,![]() .
.
For a put option, a point outside the curve in the upper region is given by ![]() for
for ![]() and
and![]() . A point on the curve is represented by
. A point on the curve is represented by ![]() for
for ![]() and
and![]() . Finally, a point outside of the curve in the lower region is given by
. Finally, a point outside of the curve in the lower region is given by ![]() for
for ![]() and
and![]() . The case of a call option is similar, we only have to invert de inequalities corresponding to S with respect to
. The case of a call option is similar, we only have to invert de inequalities corresponding to S with respect to![]() .
.
This determines the region of solution for an American option.
We now define the price of an American option in terms of the price of a European option at each time t, where![]() , multiplied by a normalizing weight
, multiplied by a normalizing weight![]() , representing the probability of attaining S at time t. Finally these values are integrated with respect to time.
, representing the probability of attaining S at time t. Finally these values are integrated with respect to time.
Mathematically, for each t, the weight![]() , corresponds to the transition probability density function, which is determined by the Fokker-Planck equation as follows:
, corresponds to the transition probability density function, which is determined by the Fokker-Planck equation as follows:
![]() (15)
(15)
calculating the the partial derivatives we have:
![]() (16)
(16)
with boundary conditions:
![]() . This condition is not necessary for the case of an American put option.4
. This condition is not necessary for the case of an American put option.4
![]() for
for![]() , where
, where ![]() is the Dirac delta.
is the Dirac delta.
![]() , where
, where ![]() is the free boundary.
is the free boundary.
The Fokker-Planck equation with respect to ![]() is defined in the rectangle
is defined in the rectangle ![]() and has boundary conditions
and has boundary conditions ![]() and
and ![]() when
when![]() . In our alternative formula, the solution region is restricted by the curve resulting from the free boundary
. In our alternative formula, the solution region is restricted by the curve resulting from the free boundary![]() .
.
![]() when
when![]() .
.
Another condition of consistency but with respect to the parameter is ![]() when
when![]() .
.
Remark 1 It is very important to keep in mind that the density ![]() does not satisfy a free boundary problem. The free boundary is given for the option price, namely, the domain in which we define
does not satisfy a free boundary problem. The free boundary is given for the option price, namely, the domain in which we define ![]() is well determined and does not depend on
is well determined and does not depend on ![]() itself.
itself.
Remark 2 The Fokker-Planck equation with respect to ![]() has an explicit solution in the log-normal case (Black-Scholes)5, and that solution is given as follows.
has an explicit solution in the log-normal case (Black-Scholes)5, and that solution is given as follows.
Let ![]() be the initial value of the underlying asset and
be the initial value of the underlying asset and ![]() the initial time. S and t are the future values. The probability that the underlying asset takes the value of S at time t, given the initial time
the initial time. S and t are the future values. The probability that the underlying asset takes the value of S at time t, given the initial time ![]() and the correspon- ding value
and the correspon- ding value ![]() is:
is:
![]() (17)
(17)
This function satisfies the Fokker-Planck partial differential equation and the backwards Kolmogorov equation.
Remark 3 The normalization for the probability density function is given by:
![]()
with
![]() (18)
(18)
Remark 4 Exercising an American call option before expiry is not optimal, because ![]() (the benefit of exercising the option is less than keeping the option), so the optimal time to exercise these options is at its maturity, therefore the value of a European option is equal to its American counterpart. This is a well known fact (see in [14] [31] [32] ).
(the benefit of exercising the option is less than keeping the option), so the optimal time to exercise these options is at its maturity, therefore the value of a European option is equal to its American counterpart. This is a well known fact (see in [14] [31] [32] ).
According to this last remark, the interesting case to study is that of an American put option, hence from now on we will focus on this case. This is not valid anymore if we consider that the S can give dividends.
3.3. American Put Option Formula
Let ![]() and
and ![]() be the European and American put option prices respectively, then we claim that the price of an American put option is
be the European and American put option prices respectively, then we claim that the price of an American put option is
![]() (19)
(19)
The probability density function ![]() satisfies the conditions mentioned above.
satisfies the conditions mentioned above.
The consistency conditions of an American put option are:
![]() .
.
![]() when
when![]() . Indeed
. Indeed
![]()
This follows from Fatou’s lemma. Notice that ![]() is bounded when
is bounded when![]() , and clearly
, and clearly![]() .
.
Moreover ![]() for
for![]() .
.
This can be proved using the fact that the price of a put option near the free boundary ![]() and considering that
and considering that![]() , can be written as:6
, can be written as:6
![]()
with ![]() (see [21] ). Then
(see [21] ). Then
![]() (20)
(20)
If we calculate the partial derivative with respect to S of the Equation (20) we get:
![]()
and consequently we have:
![]() (21)
(21)
The next subsection shows, for consistency, that the alternative formula satisfies the Black-Scholes inequality.
3.4. Consistency of the Formula with the Black-Scholes Approach
The advantage of this new formula, provided we know the location of the free boundary, is that we only need to asses the value of the function![]() , because the solution of the European option is known analytically by the Black-Scholes equation. Moreover we can introduce systematically the effect of macroeconomic factors within the valuation [30] . In general, the best way to obtain the function
, because the solution of the European option is known analytically by the Black-Scholes equation. Moreover we can introduce systematically the effect of macroeconomic factors within the valuation [30] . In general, the best way to obtain the function ![]() is numerically. First we verify, for the sake of consistency, that this new way of pricing American options is equivalent to the familiar Black-Scholes approach in the log-normal case.
is numerically. First we verify, for the sake of consistency, that this new way of pricing American options is equivalent to the familiar Black-Scholes approach in the log-normal case.
Remember that the Black-Scholes inequality for American options (see [14] ) is given by:
![]() (22)
(22)
Let![]() , then
, then
![]() (23)
(23)
Without loss of generality and to simplify the calculations, we write
![]() ,
, ![]() and
and![]() .
.
![]() (25)
(25)
Afterwards, we calculate the partial derivatives appearing in (16) and (23), and considering the value of![]() ,7 inequality (22) is transformed in:
,7 inequality (22) is transformed in:
![]() (24)
(24)
where ![]()
It is necessary to check that the left hand side of the inequality is less than or equal to zero, which we will do this next. It is straightforward to verify that all underlined terms are negative. We show that the positive terms, after an appropriate rescaling, are always of lower order than the negative ones. First we have to recall some important facts that will be useful in the proof. The term![]() , is given by the Greek letter
, is given by the Greek letter![]() , which corresponds to the expression:
, which corresponds to the expression:
![]() (26)
(26)
which is negative for the European put option with a non-dividend-paying underlying asset and
![]() (27)
(27)
This is always positive for a European call option with a non-dividend-paying asset (see [14] y [35] ). We show in Figure 3 the variation of delta of a call and put option with respect to the underlaying asset, as well as the variation of the delta with respect to maturaty time.
Hence it follows that:
![]()
![]()
Figure 3. Variation of D with respect to European options.
for a put option, and
![]()
for a call option.
Therefore, in the case of a put option, which is important for this analysis, we have![]() .
.
Lemma 1
![]()
Proof.
We proceed by contradiction.
For any![]() , it holds that
, it holds that
![]() (28)
(28)
By continuity, the integral remains being positive for any arbitrary and small ![]() such that
such that![]() , then
, then
![]() (29)
(29)
Now, we analyze each term separately.
![]()
The difference ![]() tends to zero, because
tends to zero, because ![]() is arbitrary and the functions involved are continuous, so that it can be taken as small as one likes, which makes the difference negligible.
is arbitrary and the functions involved are continuous, so that it can be taken as small as one likes, which makes the difference negligible.
For the term![]() , we have that
, we have that ![]() since it is a density function and on the other side we had that
since it is a density function and on the other side we had that![]() , then
, then
![]()
So ![]() and
and
![]()
For ![]() in (29) we know that
in (29) we know that ![]() is negative for a put option and
is negative for a put option and![]() , so
, so
![]() (30)
(30)
Although the term is greater than zero, we can make this smaller that the negative terms. This is explained with detail in remark 5.
Finally, we obtain
![]() (31)
(31)
Which is in contradiction with (28).
We therefore have the Lemma 1
![]()
Moreover, ![]() and
and ![]() so that
so that
![]()
Remark 5 It is important to note that the time ![]() depends on the free boundary
depends on the free boundary![]() , which implies that the first and second derivatives with respect to
, which implies that the first and second derivatives with respect to ![]() also depend on the free boundary. But we know that the free boundary is regular, concave, increasing and at least of class
also depend on the free boundary. But we know that the free boundary is regular, concave, increasing and at least of class![]() , which guarantees that this boundary and in turn the derivatives of
, which guarantees that this boundary and in turn the derivatives of ![]() also exist.
also exist.
Remark 6 For the positive terms of inequality (25), let m be an arbitrary large value such that
![]()
This is possible because the Fokker-Planck equation is linear and we can always rescale the solution. Also note that the valuation formula is linear with respect to![]() . Therefore we can multiply and divide by m without changing the result. In the calculation presented above, as well as in inequality (25), the positive terms scale at least as
. Therefore we can multiply and divide by m without changing the result. In the calculation presented above, as well as in inequality (25), the positive terms scale at least as ![]() and therefore can be made smaller in relation to the negative terms that are invariant under such rescaling. Notice that, there is at least one of those terms, for example, the second one in inequality (25),
and therefore can be made smaller in relation to the negative terms that are invariant under such rescaling. Notice that, there is at least one of those terms, for example, the second one in inequality (25),![]() .
.
With that we have finally proved the claim that the new way to price American options given by (19) coincides with the standard one.
Analytical Comparison with Other Methodologies
Another way to see the consistency of our proposal is to verify that the formula of Carr, Jarrow and Myneni [5] and the binomial tree method are consistent with our formula 19.
1) Carr, Jarrow and Myneni Formula
Using their notation, in a region![]() , the American put option value,
, the American put option value, ![]() , can be decomposed into the price of a European put option,
, can be decomposed into the price of a European put option, ![]() , and an early exercise premium,
, and an early exercise premium,![]() :
:
![]()
![]() (32)
(32)
and ![]() is the standard normal distribution function.
is the standard normal distribution function. ![]() is the free boundary and
is the free boundary and
![]() .
.
Then starting from the previous theorem we have:
![]() (33)
(33)
Here, ![]() ,
, ![]() and
and ![]()
2) Binomial Tree Method
It is easy to check that the standard binomial tree method can be decomposed in two steps. First, we find the exercise (free) boundary and substitute the prices by the payoff. Second, we proceed exactly as in the European case restricted to this region. This is precisely the discrete analogue of expression (19).
3.5. Application of the Alternative Formula
For verifying the efficiency of the new formula to price American options it is necessary to analyze its behavior with specific examples. For that we consider several cases, in which we estimate the American option prices and we compare those with the prices obtained with other methods, such as: the tree method (Cox, Ingersoll and Rubinstein), the finite difference method (implicit and explicit) and Longstaff and Schwartz method. For consistency, we make all calculations for the log-normal case (Black-Scholes).
Before going into details about the numerical methods, we present the algorithm by which we calculate the prices of American put options.
For an ![]() with
with ![]() fixed:
fixed:
1) In general, the probabilities are estimated using the solution of the partial differential equation (15) for various times before or equal to expiring. These probabilities for the log-normal case can be found also through the explicit solution (17).
2) Probabilities are normalized so that![]() .
.
3) Calculate the price of a European put option by the explicit Black-Scholes formula with underlaying asset S in different real times t8.
4) a) If a priori we know the free boundary, ![]() in the non early exercise region.
in the non early exercise region.
b) If the free boundary is not known, we check whether the early exercise is optimal at each time step, i.e., takes the maximum between the solution of the Black-Scholes equation ![]() and the payoff function,
and the payoff function,![]() . In other words we consider the function
. In other words we consider the function
![]()
5) Multiply the normalized probability, ![]() , by the function
, by the function ![]() for every t.
for every t.
6) Calculate the integral ![]() to determine the value of an American put option.
to determine the value of an American put option.
The flow chart for the algorithm is given in Figure 4.
With this algorithm, we describe the numerical way to solve specific examples and we compare the results, evaluated with traditional methods and our approach.
To find the numerical solution of the Fokker-Planck PDE, use the Finite Element Modeling Laboratory package (FEMLAB Multiphysics in MATLAB), which is an advanced software package for modeling and simulating many physical process that can be described through PDE's.
For the particular case, where S follows a log-normal process, we can use the explicit solution (15) to determine the probabilities![]() . The Table 1 shows the explicit solution for these probabilities and the corre- sponding numerical approximations. We consider
. The Table 1 shows the explicit solution for these probabilities and the corre- sponding numerical approximations. We consider![]() ,
, ![]() ,
, ![]() and
and ![]() for the twelve months of a year.
for the twelve months of a year.
The numerical approach is very close to the explicit probabilities. So we use both interchangeably. For practical purposes and only in this case, to verify that the new way to value American options (19) is consistent with the log-normal case (Black-Scholes), we use the closed formula (17), which was implemented in MAT- LAB.
Now, we show a concrete example according to the steps of the algorithm for pricing an American option with formula (19).
Let the asset price![]() , the exercise price
, the exercise price![]() , the riskless interest rate
, the riskless interest rate![]() , the volatility
, the volatility ![]() and the time
and the time ![]() periods, which correspond to
periods, which correspond to ![]()
![]() . In this case, we do not know the location of the free boundary. The results are showed in the Table 2.
. In this case, we do not know the location of the free boundary. The results are showed in the Table 2.
![]()
Figure 4. Flow chart to find the price of an American put option given by the formula (19).
![]()
Table 1. Explicit and numerical comparison of the probabilities (r).
![]()
Table 2. American put option values.
Source: Own calculus using, as approach to the integral, the trapezoid method.
3.6. Comparison with Other Numerical Methods
In the following examples, we estimate the American put option values by the binomial method and the finite differences (implicit and explicit), we take the Bern Arne numerical implementation Ødegaard (see [33] ), and for other methods CRR (an American option price by Cox-Ross-Rubinstein tree method calculated using the finite differences for the Black-Scholes PDE)and FD (American option price by finite differences applying to the Black-Scholes PDE). The numerical implementations of these methods were made in MATLAB (see [34] ). The New a) for boundary know, and b) for boundary not know method corresponds to our methodology for evaluating an American put option with (19). For more details on these methods, see [14] [35] .
In Table 3, in each example all involved variables are changed in the model and we do not know![]() , we take it as T.9
, we take it as T.9
If in Example 3) we consider ![]() and
and![]() , then 1) is equal to 5 and New 2) equals 4.7936. For the case that
, then 1) is equal to 5 and New 2) equals 4.7936. For the case that ![]() and
and![]() , posted a) is 5 and New b) is 4.8434.
, posted a) is 5 and New b) is 4.8434.
Finally, in Table 4 we show the formula New a) and New b) when the time changes. We can see that when the boundary is known, the price does not change. However, whether the boundary is not known the price changes and it is bigger whether t goes up.
There are other more complex numerical methods to estimate american options, within them we mention some: [3] [4] [8] [11] [27] [36] - [41] .
4. Conclusions
In conclusion we can say the following:
Mathematically, we prove that this new proposal for pricing American options is consistent with the Black- Scholes approach (canonical problem).
One application of this formula could be seen in the analytical proof that an American call option is equal to a European call option, i.e., the early exercise of an American call option is not optimal and the probability ![]() is a Dirac delta concentrated on
is a Dirac delta concentrated on![]() . This result is shown in [31] .
. This result is shown in [31] .
As an application of the new way of pricing American options, we show numerically several examples. This proposal gives adequate proxies in comparison with traditional methods, such as binomial trees (Binomial CRR) and finite differences (Explicit and Implicit).
The advantage of using this new formula is that in order to compute the price of any American option, we only need to approximate the value of the probability of staying in the requested state, provided we already know the location of the free boundary, as the value of a European put option is known explicitly, which makes it more flexible and easy to estimate.
![]()
Table 3. Comparison of an American put option.
![]()
Table 4. Comparison of an American put option.
Moreover, by obtaining the transition probabilities via the Kolmogorov equation, we have the advantage of being able to systematically incorporate the effect of macroeconomic factors, which would make the calculation of the option price more realistic.
Acknowledgements
The authors thank the Editor and the referee for their comments. The authors also appreciate the valuable comments and suggestions of Josué Cortés, Gonzalo Rangel, Patricia Saavedra, Alvaro Cartea, Gilberto Flores and the seminar participants in Banco de México. The views and conclusions presented in this paper are exclusively the responsibility of the authors and do not necessarily reflect those of Banco de México.
NOTES
2If ![]() for all i, then the Fokker-Planck equation is given by
for all i, then the Fokker-Planck equation is given by
with ![]() and
and![]() .
.
3Note that when we say that TS is the time to expiration, we mean the time corresponding to the free boundary, i.e., for each S there is a time TS on the free boundary.
4Since the origin is contained in the interior of the early exercise region.
5In general, the Fokker-Planck equation does not have explicit solutions.
6If ![]() is continuous and monotone, there exist
is continuous and monotone, there exist ![]() such that
such that![]() . Otherwise,
. Otherwise, ![]() , is exercised the option. For more details can consult [14] .
, is exercised the option. For more details can consult [14] .
7We only have to observe that the Black-Scholes equation is backwards. Then, in order to make the consistent calculations, we have to take the backwards Kolmogorov equation for![]() . For this reason we consider the following equation (making the change of variable
. For this reason we consider the following equation (making the change of variable ![]() and abusing the notation, using again t instead of
and abusing the notation, using again t instead of![]() ):
):
8A priori we do not know the location of the free boundary, which implies that the value of expiration time at the boundary TS is unknown, then for numerical calculations instead we take the expiry time T.
9The time is annual, namely, 5 months is equivalent to![]() .
. ![]() is the monthly time where the option is estimated in the New method. In the other methods (binomial, explicit, implicit, CRR, FD and LSM), the time corresponding is where
is the monthly time where the option is estimated in the New method. In the other methods (binomial, explicit, implicit, CRR, FD and LSM), the time corresponding is where ![]()
![]() .
. ![]() and
and![]() . Consider
. Consider ![]() for the time and
for the time and ![]() for the asset, except in the explicit method. In this method, we use
for the asset, except in the explicit method. In this method, we use ![]() and
and ![]() in the examples.
in the examples. ![]() and
and![]() .
.