1. Introduction
A Farey sequence of order N is a set of irreducible fractions between 0 and 1 arranged in an increasing order, the denominators of which do not exceed N. 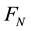 could be obtained from
could be obtained from 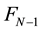 by calculating the mediant between two successive values from which it was derived. In [1] -[3] Farey graph and Farey matrix have been constructed from Farey sequence of order N. In [4] Farey partition is derived and discussed some matrix property from Farey sequence. In [5] Farey graph is introduced in iterative process. In this paper we construct Farey tri-
by calculating the mediant between two successive values from which it was derived. In [1] -[3] Farey graph and Farey matrix have been constructed from Farey sequence of order N. In [4] Farey partition is derived and discussed some matrix property from Farey sequence. In [5] Farey graph is introduced in iterative process. In this paper we construct Farey tri-
angle graph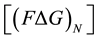 , in iterative process, and it is constructed from the method of mediant property as follows in the Farey sequence. From the co-ordinates of this graph we form a Farey triangle matrix
, in iterative process, and it is constructed from the method of mediant property as follows in the Farey sequence. From the co-ordinates of this graph we form a Farey triangle matrix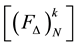 . Similarly we construct complementary Farey triangle graph
. Similarly we construct complementary Farey triangle graph 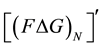 and complementary Farey triangle matrix
and complementary Farey triangle matrix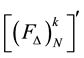 .
.
2. Farey Triangle Graph
2.1. Definition: Farey Triangle Graph: 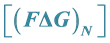
Farey triangle graph of order N is constructed from Farey Sequence. Consider X and Y axes with vertices as Farey Sequnence in . The Farey triangle graph of order N is formed from Farey triangle graph of order
. The Farey triangle graph of order N is formed from Farey triangle graph of order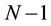 , iteratively as Farey sequence. In this graph, vertices from X to Y axis is joined only if the vertices (or Farey fractions) are same to obtain a Farey triangle.
, iteratively as Farey sequence. In this graph, vertices from X to Y axis is joined only if the vertices (or Farey fractions) are same to obtain a Farey triangle.
2.2. Construction of Farey Triangle Graph
The Farey triangle graph of order 1 begin with vertices  and
and  in both axes. The vertex
in both axes. The vertex 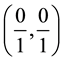 is the ori-
is the ori-
gin of the Farey triangle graph of order 1. In this graph join the vertices when X and Y axes have the same fractions to obtain a Farey triangle. ![]() is constructed from
is constructed from![]() . In this graph the vertices are inserted by the method of the mediant between each pair of consecutive fractions in both axes of
. In this graph the vertices are inserted by the method of the mediant between each pair of consecutive fractions in both axes of![]() . Si-
. Si-
milarly, we follow the same method to obtain ![]() from
from![]() . The Farey triangle graph
. The Farey triangle graph ![]() of order N can be constructed from Farey triangle graph
of order N can be constructed from Farey triangle graph ![]() by using the Farey sum operation denoted as
by using the Farey sum operation denoted as![]() . In
. In ![]() the vertices in X and Y axes are irreducible fractions in Farey sequence of order
the vertices in X and Y axes are irreducible fractions in Farey sequence of order![]() . For each edge in
. For each edge in ![]() introduced in iteration
introduced in iteration![]() ,
, ![]() could be obtained
could be obtained
from ![]() by calculating the mediant between each pair of consecutive fractions in both axes of
by calculating the mediant between each pair of consecutive fractions in both axes of![]() . Some illustrations are presented below: Figures 1-4 denote the Farey triangle graph of different order, from this graph we define Farey triangle matrix.
. Some illustrations are presented below: Figures 1-4 denote the Farey triangle graph of different order, from this graph we define Farey triangle matrix.
In the above illustrations, the like coloured lines denote the edges inserted in successive iterations.
![]()
Figure 1. Farey triangle graph of order 1.
![]()
Figure 2. Farey triangle graph of order 2.
![]()
Figure 3. Farey triangle graph of order 3.
![]()
Figure 4. Farey triangle graph of order 4.
2.3. Farey Triangle Matrix
Let ![]() be a Farey triangle. The vertices of the triangle are clearly Farey fractions. Let the abscissa be
be a Farey triangle. The vertices of the triangle are clearly Farey fractions. Let the abscissa be ![]() and ordinate
and ordinate![]() , we obtain
, we obtain
![]()
The Farey triangle graph forms a matrix [6] ,
![]()
where a and b are the numerator of Farey fractions and c denote the order of the Farey sequence. k denote the number of vertices inserted to move from ![]() to
to![]() .
.
Illustrations
1) Farey triangle matrix of order 2.
![]()
2) Farey triangle matrix of order 3
Farey triangle graph of order 3 is derived from Farey triangle graph of order 2. Here two vertices are inserted, so two Farey triangle matrices are constructed.
![]()
2.4. Theorem
The sum of the determinants of the Farey triangle matrices of prime order is given by
![]()
Proof:
In Farey triangle graph of prime order![]() ,
, ![]() vertices are introduced.
vertices are introduced.
The ordinates![]() ;
; ![]() are connected only if
are connected only if ![]() and it forms a matrix
and it forms a matrix
![]() where
where
The sum of the determinant of these matrices is
![]()
![]()
2.5. Theorem
The sum of Farey triangle matrices of prime order is![]() .
.
Proof:
The Farey triangle matrices of prime order
![]()
where![]() .
.
![]()
![]()
![]()
![]()
3. Complementary Farey Triangle Graph
3.1. Definition
The complementary Farey triangle graph ![]() of order N is a Farey triangle with edges as the line joining vertices whose numerators are complementary with respect to the order of the graph and it forms complementary Farey triangle.
of order N is a Farey triangle with edges as the line joining vertices whose numerators are complementary with respect to the order of the graph and it forms complementary Farey triangle.
3.2. Construction of Complementary Farey Triangle Graph
The complementary Farey triangle graph ![]() of order
of order ![]() can be constructed from complementary Farey triangle graph
can be constructed from complementary Farey triangle graph![]() . The vertices are inserted as in Farey triangle graph. In this graph the
. The vertices are inserted as in Farey triangle graph. In this graph the
vertices are connected if the sum of the numerators of the fractions in each vertices of X and Y axis is equal to the order of the complementary Farey triangle graph. In complementary Farey triangle graph of order 2, we be-
gin with vertices ![]() and
and ![]() in both axes. The vertex
in both axes. The vertex ![]() is the origin of the complementary Farey
is the origin of the complementary Farey
triangle graph. In this graph the vertices are inserted by the method of the mediant between each pair of consec-
utive fractions in both axes of![]() . We follow the same method to obtain
. We follow the same method to obtain ![]() from
from![]() .
.
Figures 5-7 denotes the complementary Farey Triangle Graph of different orders, from this graph we define Complementary Farey Triangle Matrix. Some illustrations are presented below:
3.3. Complementary Farey Triangle Matrix
The vertices of the complementary Farey triangle namely Farey fractions are used to construct this matrix. Let the abscissa be ![]() and ordinate
and ordinate![]() . Join these vertices to form a complementary Farey triangle graph and correspondingly complementary Farey triangle matrix as given below.
. Join these vertices to form a complementary Farey triangle graph and correspondingly complementary Farey triangle matrix as given below.
![]()
Figure 5. Complementary Farey triangle graph of order 2.
![]()
Figure 6. Complementary Farey triangle graph of order 3.
![]()
Figure 7. Complementary Farey triangle graph of order 4.
![]()
where a and b are the numerator of Farey fractions and c denote the order of the Farey sequence. k denote the number of vertices inserted to move from ![]() to
to![]() .
.
3.3.1. Illustrations
1) Complementary Farey triangle matrix of order 2.
![]()
2) Complementary Farey triangle matrix of order 3
![]()
3.3.2. Remark
![]() .
.
3.4. Theorem
The sum of determinants of the complementary Farey triangle matrices of prime order p is
![]()
Proof:
Consider the complementary Farey triangle matrices of prime order.
![]() ;
;
where ![]()
![]()