Alternative Derivation of the Mean-Field Equations for Composite Fermions ()
1. Introduction
The study of low-dimensional electron systems is a topic of great current interest in condensed matter. Under certain conditions, three-dimensional solids can behave as pseudo two or one-dimensional quantum systems. Among other things, this is because these systems have special characteristics which lead to phenomena such as superconductivity of high critical temperature and some magnetic properties, with potential technological applications.
Since a long time ago, the phenomenon of high-temperature superconductivity is being considered with increasing interest. The current status of knowledge on this subject does not allow establishing on firm foundation this phenomenology. Different approaches are used to address this issue. A promising approach is based on models using composite particles [1] [2] . In Ref. [1] , Jain and Anderson propose the existence of an underlying connection between the resonating valence bond theory for high-temperature superconductivity and the composite fermion theory for the fractional quantum Hall effect [3] -[5] . Besides, in Ref. [2] , Lu, Das Sarma and Park relate the superconductivity with the quantum Hall effect through the formation of Cooper pairs of composite fermions.
A manner of studying these systems is based on quantum field theory. Another manner is to use quantum many-body theory [6] [7] , implemented by using analytical and computational techniques.
In Refs. [8] [9] , we have proposed models of composite particles and we have studied them by using the first mechanism cited in the previous paragraph. These models are generalizations of the models discussed by means of the second mechanism in Refs. [10] -[12] .
To deal with models that consider the electromagnetic interaction of composite fermions, a phenomenological Hamiltonian is commonly used. In this paper, by using the standard methods of field theory, we show that the same Hamiltonian can be reached.
In this context, our purpose is to relate the results of Refs. [8] [9] with the ones corresponding to Ref. [10] , by using the usual techniques of field theory. In particular, we use the Dirac Hamiltonian formalism for constrained systems. In this way, we show that this procedure leads to the same results as the ones obtained by means of the phenomenological models of condensed matter. For example, the Coulombian interaction density which appears in the standard formulation [10] is deduced from the formalism. Moreover, from the constraint structure, we determine the relation between the electron-density distribution and the magnetic flux quanta.
Besides, we show that the inclusion of a topological mass term for the electromagnetic field in the Lagrangian density introduces interaction terms absent in the original canonical Hamiltonian.
The paper is organized as follows. In Section 2, we show how to obtain the canonical Hamiltonian from the starting Lagrangian. Then, in Section 3, we see what happens when we add a topological mass term for the electromagnetic field in the Lagrangian. Finally, in Section 4, we display our conclusions.
2. Formalism
We consider a classical nonrelativistic field theory with U(1) × U(1) gauge symmetry in 2 + 1 dimensions for the electromagnetic interaction of electrons. This model uses a Chern-Simons (CS) U(1) gauge auxiliary field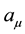 .
.
In order to describe this interaction, we propose the following singular Lagrangian density:
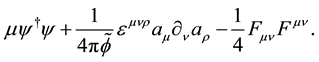 (1)
(1)
The Greek indices take the values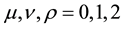 . We use natural units where
. We use natural units where . The Minkowski metric is
. The Minkowski metric is  and
and . The covariant derivative involving both the CS field and the electromagnetic field is written as
. The covariant derivative involving both the CS field and the electromagnetic field is written as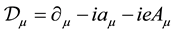 , and we design
, and we design . Furthermore,
. Furthermore,  is the electromagnetic field tensor.
is the electromagnetic field tensor.
The matter field  is a charged spinorial field which describes electrons with charge
is a charged spinorial field which describes electrons with charge  and band mass
and band mass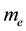 . The chemical potential of the electrons is
. The chemical potential of the electrons is . The constant
. The constant 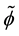 introduced in the Lagrangian density, will be determined later.
introduced in the Lagrangian density, will be determined later.
The independent dynamical field variables are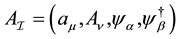 , and their corresponding canonically
, and their corresponding canonically
conjugate momenta, defined by , are
, are![]() . In these expressions, the Greek in-
. In these expressions, the Greek in-
dices take the values![]() .
.
The canonical Hamiltonian density, defined as![]() , reads
, reads
![]() (2)
(2)
where the Latin indices take the values![]() .
.
As usual, the relations between the fields and the momenta not depending on the velocities lead to primary constraints. Thus, the momentum ![]() does not generate any constraints. By applying the consistency condition on the primary constraint, we found the secondary constraints.
does not generate any constraints. By applying the consistency condition on the primary constraint, we found the secondary constraints.
Finally, classifying the total set of constraints, we find the first and second-class constraints. The first-class constraints are
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
while the second-class ones are
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
We choose the following gauge-fixing conditions, which are consistent with the equations of motion:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
The algebraic development corresponding to these results were performed in Ref. [8] .
As it is well known, one can define the Dirac brackets from the Bose-Fermi ones, and then all the equations of the theory are formulated taking into account the former brackets, as it can be seen in Ref. [8] . Once we impose the Dirac brackets, the first and second-class constraints and the gauge-fixing conditions can be set strongly equal to zero. In this way, these equations become identities expressing some canonical variables in terms of the others, that is,
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
It is worth to mention that, in order to obtain Equation (15) from Equation (13), we have substituted the logarithmic interaction [9] , characteristic of a strict two dimensional space, by the standard Coulombian [13] . This is justified because the electrons are confined to move in two dimensions, but interact each other in a world of three dimensions.
By replacing the momenta of Equations (19) and (20) in Equation (4), we get![]() . In this way, the scalar potential of Equation (15) becomes
. In this way, the scalar potential of Equation (15) becomes
![]() (21)
(21)
The term ![]() that appears in the original Lagrangian density (1), gives rise to the Coulombian interaction density. In the standard formulation [10] , this term is added ad hoc.
that appears in the original Lagrangian density (1), gives rise to the Coulombian interaction density. In the standard formulation [10] , this term is added ad hoc.
Taking the spatial derivative of the momentum ![]() given by Equation (17) and replacing it in Equation (3), we obtain the following identity:
given by Equation (17) and replacing it in Equation (3), we obtain the following identity:
![]() (22)
(22)
In Ref. [10] , this equation is considered as a constraint of the theory. In the Lagrangian density (1), this constraint appears multiplied by![]() , which plays the role of Lagrangian multiplier.
, which plays the role of Lagrangian multiplier.
The curl of the CS field is linked with a magnetic field in the form![]() . From Equation (22), it can be seen that the distribution of the CS magnetic field coincides with that of the electron-density. Thus, the relation between the electron-density distribution and the magnetic flux quanta stayed determined.
. From Equation (22), it can be seen that the distribution of the CS magnetic field coincides with that of the electron-density. Thus, the relation between the electron-density distribution and the magnetic flux quanta stayed determined.
Therefore, the Lagrangian density (1) describes a composite fermion system, where ![]() is the strength of the flux tube, in units of the flux quantum
is the strength of the flux tube, in units of the flux quantum ![]() [13] . As a consequence, the composite fermions behave as free fermions in an effective magnetic field
[13] . As a consequence, the composite fermions behave as free fermions in an effective magnetic field![]() , where
, where ![]() is the physical magnetic field. In the mean field approximation, the field
is the physical magnetic field. In the mean field approximation, the field ![]() is constant and uniform [13] .
is constant and uniform [13] .
Replacing all previous results in Equation (2), we obtain
![]() (23)
(23)
where
![]() (24)
(24)
Since the field ![]() verifies the Coulomb gauge (11), the vector potential becomes transversal, and then it can be proved that
verifies the Coulomb gauge (11), the vector potential becomes transversal, and then it can be proved that
![]() (25)
(25)
with
![]() (26)
(26)
where ![]() and
and![]() .
.
Besides, following Ref. [14] , but taking into account that we are working in 2 + 1 dimensions, the electric field can be split in its transversal and longitudinal components in the plane of electron motion![]() , where
, where ![]() and
and![]() . Thus,
. Thus,
![]() (27)
(27)
where B is perpendicular to the motion plane.
Finally, we can write
![]() (28)
(28)
Usually, when only an external uniform magnetic field is considered, the canonical Hamiltonian reduces to
![]() (29)
(29)
3. Addition of a Topological Mass Term for the Electromagnetic Field
As it is well known, the addition of the CS term to the Maxwell action leads to the topologically massive (2 + 1)-dimensional electrodynamics [15] . In this theory, a modified Gauss law appears. As a result, any charged particle carries a magnetic flux proportional to its charge.
In this section, we analyze the differences that appear with respect to the original model when a topological mass term for the electromagnetic field is added to the Lagrangian density ![]() given by Equation (1)
given by Equation (1)
![]() (30)
(30)
where ![]() is the topological mass and
is the topological mass and ![]() is the magnetic flux attached to the electrons.
is the magnetic flux attached to the electrons.
In this case, the canonical Hamiltonian density becomes
![]() (31)
(31)
where ![]() is given by Equation (2), and now
is given by Equation (2), and now![]() .
.
The only first-class constrains that change with respect to the previous ones are
![]() (32)
(32)
![]() (33)
(33)
In the same way, the only gauge-fixing condition that changes is
![]() (34)
(34)
These results have been formally demonstrated in Ref. [9] .
Following the same steps like in the previous section, it can be proved that the constraint (22) remains valid.
In contrast to Equation (15), ![]() is now determined by
is now determined by
![]() (35)
(35)
Finally, the topological massive canonical Hamiltonian density is
![]() (36)
(36)
By replacing ![]() of Equation (35) in Equation (36), we can related this Hamiltonian density with the corresponding one of the previous section
of Equation (35) in Equation (36), we can related this Hamiltonian density with the corresponding one of the previous section
![]() (37)
(37)
where ![]() is given in Equation (28).
is given in Equation (28).
Once we integrate Equation (37), the first two terms give the same contributions to the Hamiltonian. By considering the constraint (22), these terms can be associated to the interaction between the external and CS magnetic fields mediated by the distance. In the limit of infinite topological mass, this interaction vanishes. This is consistent with the fact that in the usual formulation, where the external magnetic field is uniform, this interaction is not present. The last term in Equation (37) represents the self interaction of the external magnetic field in a higher order in the topological mass.
4. Conclusions
By means of a classical nonrelativistic U(1) × U(1) gauge field model for the electromagnetic interaction of electrons, we have shown how to find the mean-field Hamiltonian describing composite fermions in 2 + 1 dimensions. For this purpose, the Dirac Hamiltonian formalism for constrained systems was considered.
Furthermore, in Section 2, we showed how the Coulomb interaction naturally appears while in the usual formulation it is introduced ad hoc. In the usual formulation, Equation (22) is taken as a constraint of the theory. In this paper, we derived its validity from the constraint structure.
Finally, in Section 3, we saw that the inclusion of a topological mass term for the electromagnetic field in the Lagrangian density introduces interaction terms absent in the canonical Hamiltonian (29).
Acknowledgements
The authors acknowledge Dr. R. Id Betan for his invaluable contribution and helpful discussions.