1. Introduction
Sir Arthur Eddington [1] made a significant effort in the 1930’s to find underlying connections between the constants of Physics. This effort defined the problem, but did not lead to significant results. The problem of dealing with arbitrary units in fundamental Physics still exists.
2. Unitless Physics
The standard view is that the fundamental constants of Physics are independent, that Gravity and the Electrostatic force are unrelated, and that there is no underlying structure to Standard Physics. This paper presents a unitless transformation which enables the possibility of perceiving intimate relationships between the fundamental constants, defines a relationship between Gravity and the Electrostatic force, and provides the basic parameters for the internal information processing structure of particles.
In this transformation are four constants in terms of units and three constants which are unitless. Constants with units are not really fundamental as the units have arbitrary origins. The transformation will reduce all seven constants to a unitless intimately related form.
The required constants (MKS) from N.I.S.T. 2010:
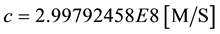
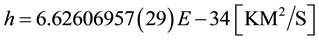
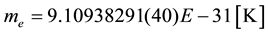
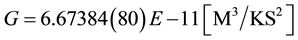
Note that the inverse of the fine structure constant has been defined as “@” and the proton/electron mass ratio is defined as “R”.
The ratio of the electrostatic force to the gravitational force in the Hydrogen atom:
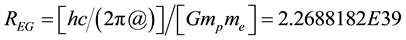 (1)
(1)
For  Schlamminger [2]
Schlamminger [2] 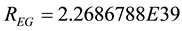
This describes the ratio of the electrostatic force to the gravitational force in terms of seven fundamental constants.
STEP 1: The value of the gravitational constant is: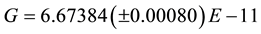 . We will adopt a different value,
. We will adopt a different value, 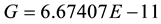 , to explore a numerical equivalence. This hypothetical value is 1.00003 larger and well within the error. It is also 1.00003 smaller than the Schlamminger measurement and equal to the 1-sigma error. This value comes from the following equation:
, to explore a numerical equivalence. This hypothetical value is 1.00003 larger and well within the error. It is also 1.00003 smaller than the Schlamminger measurement and equal to the 1-sigma error. This value comes from the following equation:
 (2)
(2)
Hereafter, we refer to this ratio as REG.
Although the equivalence term seems meaningless in terms of Standard Physics, it acquires meaning after the unitless transformation in the deBroglie frequency, the Einstein emission coefficient, and the mean lifetime of the neutron. The expression  is regarded as an information representation related to the internal processing of the Laws of Physics.
is regarded as an information representation related to the internal processing of the Laws of Physics.
REG represents the ratio of . For the same mer, REG is the ratio of
. For the same mer, REG is the ratio of .
.
 .
.
This equivalence is remarkable in its simplicity and allows development of a unitless transformation of four physical constants on the left in “2”. Physics is the search for coincidence that produces order. The addition of a “δG” may be eventually required with refinement of “G” measurements.
STEP 2: Transform to a unitless solution.
Equation (2) allows for unitless solutions for G, h, c, and me. Any solution will produce a valid mathematical transformation of Physics which will allow unitless computation. Some solutions can reduce the number of physical constants. We have chosen the solution which appears most physically significant, that is, which provides insight into underlying Physics.
The solution that has been chosen applies primarily to the left side of the equation, but allows later development of the meaning of the right side. Therefore, only the value of  is required in the transformation. The significance of this term is considered later in the paper.
is required in the transformation. The significance of this term is considered later in the paper.
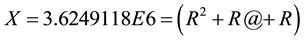
The following symbols will be used to represent the force constants: ![]()
Underlined symbols designate unitless values which are assumed to be the real internal physical values. This transformation is designated Unitless Solution Nine (US9).
Hypothesis #1: Let ![]() then
then ![]() becomes:
becomes:
![]()
Thus: ![]() with
with ![]()
Equation (2) becomes, from the standard definition of “e”:
![]() (3a)
(3a)
![]() (3b)
(3b)
Hypothesis #1 has already produced an amazing simplification of Physics which must be confirmed by similar behavior in all of Physics.
Hypothesis #2: Let:
![]() and
and ![]() (4)
(4)
Then Equations (3) become:
![]() (5a)
(5a)
![]() (5b)
(5b)
![]() (5c)
(5c)
These hypotheses have resulted in the gravitational constant to be the inverse product of the proton mass and h-bar, a new relationship in physics. Also, ![]() and
and![]() .
.
It is interesting that ![]() appears dominant in this solution and carries the role of a 3-D internal information capacity.
appears dominant in this solution and carries the role of a 3-D internal information capacity.
Then:![]() (6)
(6)
See (6b), (7) and (8) for related values.
In the Hydrogen atom:
The Bohr radius:![]() . US9:
. US9:![]() .
.
![]()
The designation in “4” separates the velocity of light into its spatial and temporal components in the Bohr atom radius. In US9, the fine structure constant becomes an element of time. See “10.” for a related topic.
In the ground state orbit of Hydrogen using US9, the light time over the radius equals the β value of the electron circular velocity.
![]()
The mysterious expression in “6.” was not required for most of the relationships in this paper. The transformation could have started with![]() . However, as noted at several points in the paper, there is possible evidence that the expression has physical significance. It would be unwise to simply void “6.” as a meaningless coincidence. Planck did not do that with “h”.
. However, as noted at several points in the paper, there is possible evidence that the expression has physical significance. It would be unwise to simply void “6.” as a meaningless coincidence. Planck did not do that with “h”.
The internal processing of particles is not expected to look similar to the external description (Standard Physics). The expression ![]() is to be regarded as a clue to the information structure of internal processing. This structure may have similarities to the machine language in modern computers where all information is in equivalent bits and the mass, time and space elements are separated by logical structure. Presumably, the symmetry rules of Standard Physics will guide development of the logical internal structure.
is to be regarded as a clue to the information structure of internal processing. This structure may have similarities to the machine language in modern computers where all information is in equivalent bits and the mass, time and space elements are separated by logical structure. Presumably, the symmetry rules of Standard Physics will guide development of the logical internal structure.
STEP 3: Solve for the conversion constants back to the MKS system:
US9 conversion constants:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
These constants are to be multiplied times the unitless values to obtain measured values in MKS units.
![]()
The value of ![]() can be adjusted to meet any improvement in the determination of the gravitational constant with only minor adjustments in the remainder of this paper.
can be adjusted to meet any improvement in the determination of the gravitational constant with only minor adjustments in the remainder of this paper.
This transformation is designated Unitless Solution Nine (US9). The argument for reality of US9 is the simplicity of the system and the new relationships between fundamental parameters which cannot be undone.
US9 is a system which simply relates electrostatics to gravity, provides a numerical value to mass which may be interpreted as an information quantity ( possible combinations ), and relates the velocity of light to the fine structure constant. The seven fundamental constants have been reduced to four. The presence of Planck’s constant in many equations increases its fundamental stature.
US9 establishes unambiguously that the fundamental constants are intimately related. This relationship is probably inherent in the internal processing logic of the Hydrogen atom and of all evolutionary descendants. It follows that internal processing produces communication fields and the particle’s reaction to external fields. US9 provides real numbers to represent the masses of fundamental particles; such values are presumed to be physical, enabling direct connection into internal structure.
The Schroedinger solution of the Hydrogen ground orbits and the Uncertainty Principle indicate that within the sphere of radius, a0, definition of position and momentum is undefinable.
In US9, ![]() , indicating that velocity and position uncertainties are of similar values. Noting that
, indicating that velocity and position uncertainties are of similar values. Noting that ![]() in US9 is very similar to the possible U.P. values. Therefore, it is assumed that all processes within a0 are a part of the internal processing of the Hydrogen atom.
in US9 is very similar to the possible U.P. values. Therefore, it is assumed that all processes within a0 are a part of the internal processing of the Hydrogen atom.
This completes the derivation of US9.
The remainder of this paper consists of applications of US9 to various topics in Physics.
Interesting quantities:
Note that h-bar is a quantity close to the number of combinations in a Rubick’s Cube.
Note that ![]()
![]()
![]()
![]() Proton mass combines gravity and quantum mechanics.
Proton mass combines gravity and quantum mechanics.
For the proton, the deBroglie frequency:![]() .
.
US9:![]() .
.
It is apparent that ![]() and
and ![]() are frequency terms in US9.
are frequency terms in US9.
![]()
This is a factor of 44 above the W boson lifetime. ![]()
From 6.:![]() (6b)
(6b)
The deBroglie frequency of the proton is related to the mass of the electron. This has implications regarding the communication between proton and electron.
![]() Rest mass energy can be an internal rate in US9.
Rest mass energy can be an internal rate in US9.
![]()
The ratio of the energy associated with the deBroglie frequency of the proton to the frequency associated with rest mass:![]() .
.
The information processing rate for the Hydrogen atom is ![]() or
or
![]() per 1.28808857E−21 sec. or 8.750594931E22 per 1.28808857E−21 sec.
per 1.28808857E−21 sec. or 8.750594931E22 per 1.28808857E−21 sec.
Einstein “A” coefficient: ![]()
US9: ![]()
![]()
![]()
![]() (7)
(7)
It is remarkable that the first term is similar to that in 6b. Increasing 0.836 to 1.00 results in![]() .
. ![]() is obviously a frequency in US9.
is obviously a frequency in US9.
Many properties associated with internal processing are temporal, resulting from a synchronous relationship with external communications.
If ![]() is considered also as an internal time parameter,
is considered also as an internal time parameter, ![]()
The mean lifetime of the neutron:
![]() (8)
(8)
In the Hydrogen atom for circular orbits using Bohr atom notation and US9:
![]()
![]()
For n = 1, US9 echoes the Uncertainty Principle;![]() ; equivalent quantities may be indistinguishable internally. The ground state of the Hydrogen atom is part of the internal information processing structure.
; equivalent quantities may be indistinguishable internally. The ground state of the Hydrogen atom is part of the internal information processing structure.
![]() = US9 Bohr radius/time therefore @ is a frequency thus giving some meaning to the term
= US9 Bohr radius/time therefore @ is a frequency thus giving some meaning to the term![]() .
.
![]() is a fundamental time increment in US9.
is a fundamental time increment in US9.
Malcolm MacGregor [3] has demonstrated that particle masses and lifetimes are definable in terms of the fine structure constant.
The circular orbital period in the Bohr atom:![]() .
.
![]()
In the ground state, electron kinetic energy is the same quantity as electron spin.
Bohr magneton:![]() .
.
The DeBroglie wavelength of the electron:![]() .
.
The DeBroglie frequency of the electron:![]() .
.
The frequency here contains the square of our fundamental frequency @.
US9 enables inquiry into whether fundamental particles have an internal information structure.
The amplitude for photon absorption by an electron:![]() .
.
![]()
![]() Hypothesis # 1
Hypothesis # 1
![]() inverse square law
inverse square law
These relations imply a common internal information process.
3. Conclusions
Gravitation, electrostatics and quantum mechanics can be related by a simple unitless transformation. The transformation has produced specific quantities which enable the application of an information based theory. It is important to realize that the mathematical relationships in this paper are an inescapable fact. The mathematics of the unitless transformation exists regardless of the means of derivation. Physics is the search for coincidence that produces order.
Digital calculations internal to particles result in the creation of external fields and the reaction of the particles to the fields of Standard Physics. This allows a balance between external fields and internally generated actions. This is a concept inherent in conservation of momentum and energy.
There are many connections revealed by US9 that are not recognizable in Standard Physics:
The electrostatic force constant in the Hydrogen atom is the inverse square of the gravitational force constant in the Hydrogen atom. ![]()
Newton’s constant of gravitation is the inverse of the product of proton mass and h-bar, Planck’s constant.![]() :
: ![]() (The first definition of the proton/electron mass ratio).
(The first definition of the proton/electron mass ratio).
The velocity of light is equal to the mass of the electron divided by the fine structure constant.
![]()
In US9, the fine structure constant is an internal time parameter.
The mass of the electron cubed is equal to h-bar. Planck’s constant is a function of electron mass.
![]()
The deBroglie frequency of the proton is simply related to the electron mass and the amplitude for photon absorption by an electron.
![]()
4. Additional Applications of US9
4.1. E&M Transformed to the Unitless Solution (US9)
US9 quantities are underlined.
Permissivity of free space: ![]()
Permeability of free space: ![]()
![]()
![]()
Transform to the unitless Solution:
1 coulomb = 6.241509343E18 electron charges for 1 charge, define ![]() unitless, therefore
unitless, therefore ![]()
![]()
![]()
![]() (9)
(9)
This exercise confirms that US9 represents reality.
![]() where
where ![]() is the electrostatic force constant.
is the electrostatic force constant.
![]() (10)
(10)
US9 produces meaningful terms for ![]() and
and ![]() . The @ comes from
. The @ comes from ![]() while the
while the ![]() comes from
comes from![]() . This is interesting support for Hypothesis #2,
. This is interesting support for Hypothesis #2,![]() .
.
This has implications for E&M theory: ![]()
![]()
![]()
Checking![]() :
:
![]()
The precision of the transformations above depends critically on the value of![]() .
.
This can be interpreted as proof of the validity of US9.
4.2. Blackbody Energy
Boltzmann’s constant: ![]()
![]()
Transform to US9: ![]() where the Kelvin temperature scale transform is not yet defined.
where the Kelvin temperature scale transform is not yet defined.
Transform the Kelvin scale via the Bohr first orbit kinetic energy:
![]()
![]()
This is the temperature which would produce an average kinetic energy in an ideal gas that is equal to that of the Hydrogen ground level.
US9: ![]()
![]()
We define the US9 value:![]() .
.
![]()
We can complete the transform of Boltzmann’s constant:
![]() (11)
(11)
Looking from the US9 point of view:
![]() becomes:
becomes:
![]() and
and![]() mean
mean![]()
![]()
![]()
![]() (12)
(12)
![]()
This may be a significant result. For![]() .
.
Also, ![]() can be the number of communicating baryons in the observable Universe.
can be the number of communicating baryons in the observable Universe.
Thus, in the US9 system, ![]() has a strong connection to fundamental physics and cosmology.
has a strong connection to fundamental physics and cosmology.
The total energy radiated by a blackbody at 105276.7 [K] or ![]() becomes:
becomes:
![]()
![]()
Note that using the first Bohr orbit kinetic energy brings ![]() near to unity.
near to unity.
![]()
![]()
Assuming that the cosmic background temperature could be related to the base energy of the Hydrogen atom, we search for possible relationships:
![]()
![]()
![]()
All three are close to fundamental terms. This may be a fundamental clue for cosmology.
4.3. Wien Displacement Law
![]() (at maximum of Mλ curve)
(at maximum of Mλ curve)
![]()
![]()
US9 has produced a close relationship between temperature and h-nu at maximum.
For ![]()
![]()
![]()
for ![]()
![]()
![]()
![]()
Again, we arrive at very simple expressions which contain fundamental constants.
US9 has been shown to be applicable to classical physics with direct interaction between all components of fundamental physics. A direct interaction with high energy physics will be demonstrated below. Two Tables are shown with good correspondence to US9 constants for the measured masses and lifetimes of fundamental particles.
Conversion of particle lifetimes and masses to US9
The US9 conversion factors are used to produce the following two tables (Table 1 & Table 2).
![]()
![]()
mean lifetime of the neutron = 880 sec. = 0.764ħKS
![]()
![]()
In Table 1, the low coefficients in the last column are much below that expected (≤68) for changes of 137 in the US9 representation. There is no sign of a gradient in the coefficients over the enormous range.
This is a surprise indicating that the US9 representation is giving close to the actual values of mass times lifetime. This depends on the US9 value of “me”, verifying its fundamental relationship to physical reality. The presence of “R” indicates that proton/electron mass ratio plays a fundamental role in particle physics, especially in the case of the bosons. We have a potential rationale for the value of “R”.
In US9, R, me and @ are components of internal temporal processing in particles. This unexpected correlation should lead directly to internal processing algorithms.
![]()
Table 1. Conversion of 21 particle lifetimes and masses to US9.
![]()
Table 2. Conversion of 28 particle lifetimes and masses to US9.
All of the following US9 terms can be incorporated into the MΔt (US9) values:
![]() This may be of value as the US9 theory of internal particle information processing is developed.
This may be of value as the US9 theory of internal particle information processing is developed.
MΔt is normally associated with the Uncertainty Principle. The large range in values, 6.050E29, requires explanation.
In Table 2, “R” is required in the particle masses but not in the lifetimes. This is a critical statement for the internal structure of the proton. The coefficients show no signs of gradients but appear to be separable into four categories. The coefficients of lifetime and mass are of similar size.
The quark masses fit the general particle pattern with three of the quarks in group 3.
The similarity in US9 coefficient means and rmsr values in both Tables is remarkable. There are no obvious distinctions between mesons and baryons.
5. Summary
The fundamental constants have been related by a simple algebraic unitless transformation. These relationships cannot be undone. A deeper understanding of the source of the Laws of Physics will result. The transformation has been applied to several areas of Physics and in every case has produced simplification and deeper meaning. US9 implies internal particle processing which produces fields and reactions to external fields. Suggestions regarding internal information states are planned for future papers.
Digital calculations internal to particles result in the creation of external fields and the reaction of the particles to the fields of Standard Physics. This allows a balance between external fields and internally generated actions. This is a concept inherent in conservation of momentum and energy.
There are many connections revealed by US9 that are not recognizable in Standard Physics:
The gravitational force constant in the Hydrogen atom is the inverse of the square root of the electrostatic force constant in the Hydrogen atom. ![]()
Newton’s constant of gravitation is the inverse of the product of proton mass and ħ, Planck’s constant.
![]()
The velocity of light is equal to the mass of the electron divided by the fine structure constant.
![]()
In US9 the fine structure constant is an internal time parameter.
The mass of the electron cubed is equal to h-bar. Planck’s constant is a function of electron mass.
![]()
Evaluation of E&M theory has resulted in redefinition of the permissivity and permeability constants.
![]()
In![]() ,
,![]() . (a connection with cosmology?)
. (a connection with cosmology?)
Fundamental particle masses are expressed in terms of me, @ and R.
Fundamental particles lifetimes are expressed in terms of me and @.
In MΔt, the bosons are intimately related to R.
The results with fundamental particle masses and lifetimes will lead to exploratory development of internal processing algorithms.
The proton and electron are the primary constituents of all activity in the Universe. The Standard Model finds that the interior of the proton is a state of total chaos and cannot build an interior structure rationale for the mass of the proton. The Standard Model deals primarily with fields, and excludes an adequate internal structure for fundamental particles. The Standard Model is one-half of a good theory, looking for its other half. US9 provides the route to the internal half.
All fundamental particles respond to force fields via quantized motion or internal action.
Such reactions are determined by internal processing and communications. The Uncertainty Principle, Momentum and Energy Conservation, and the production of Force Fields are all determined by internal processing. It is not possible to determine internal structure solely by high energy interactions which destroy internal structure.
US9 is a different viewpoint on fundamental Physics which should provide new options to physicists interested in expanding the Standard Model.