Supply Chain Commitment Contract Model Based on Uncertainty Theory under Uncertain Market Information ()
1. Introduction
The uncertainty theory [1] has been developed and improved constantly for more than ten years, since Professor Liu Baoding, Tsinghua University and his team put forward it. Its theoretical system was recognized and accepted gradually by the majority of scholars and experts, and part of them have put themselves in studying this theory [2] [3] . At present, axiom system of the theory has been established on the whole, and its theoretical system has been extended to planning theory, risk analysis, reliability analysis, logical reasoning, differential equations, statistics and differential and integral calculus and other fields. Its scope of application is expanding gradually; it has many examples of applications and the potential for further development in the fields of business, social, economic and financial. This paper considers applying the uncertainty theory to problems of the supply chain, to convert problem of random demand in the supply chain to that of uncertainty demand. At the beginning of entering the market, we do not know the actual needs of some items. Production enterprises can only accord to the experience and some experts predict if they want to grasp the market demand. Therefore, from this perspective, uncertain demand is closer to the actual than random demand. The problem of supply chain is old, and its earliest research can be traced back to 1888 when economist Edgeworth studied the supply chain shape, newsboy model [4] , with sales activities of seasonal merchandise which is more standard simplified. In the 1950s, with most of the lack of production and living materials because of the war, newsboy model and more complex models gradually became the object of research scholars, and was widely used in production of various industries [5] . Price effects were first introduced in newsboy model by Whitin [6] . The relationship between demand function and price made the sales price become one of the decision variables. Schweitzer and Cachon [7] analyzed the newsboy with preference on policy makers and found that the decisions were different from policy makers with different risk appetite, algorithms, forecasting and other factors, and thus the profits deviated from maximum profit to a certain extent. Porteus [8] , Silver [9] and some others summarized the newsboy model.
With further research, we got to know and researched Stackelberg game behavior in the supply chain and problems of supply chain coordination generated. Malone and Crowston [10] made the definition of supply chain coordination that was interdependence between the various acts of management. Hoppe [11] gave the definition of a coordinated multi-dimensional model based on the definition of Malone, enabling simultaneous information flow, logistics, and capital flow coordination, which could implement information flow, logistics, and capital flow coordination at the same time. Cachon [12] turned to the most simple newsboy model, continually improved the model and made it more complex. For an example, the wholesalers regard selling price and order quantity as decision variables. He expanded his study from the system of a manufacturer and a retailer to the system of a manufacturer and multiple retailers; retailers that face infinity and the uncertainty of market demand can be the constant replenishment instantaneously from the manufacturer and so on. These kinds of circumstances of supply chain coordination are discussed. He also discussed the supply chain coordination in these cases. Ying Wei and Tsan-Ming Choi [13] analyzed its mean-variance under the supply chain coordination mechanism of the Wholesale Pricing Contract and Profit Sharing Contract in another way and noted that Stackelberg game had a unique equilibrium point under the decentralized decision when the supply chain took such a mechanism. Cai Jianhu [14] gave the definition of flexibility contracts after studying a variety of supply chain contracts: the supply chain contract that could achieve the entire supply chain coordination while owing the capacity of distributing the gross profit of the supply chain between supply chain members in any way, and further illustrated the Order Quantity Contract, the Wholesale Price Contract and Revenue Sharing Contract are flexible contracts.
Numerous studies illustrate that it is indeed effective strategy that using such Revenue Sharing Contract, Quantity Flexibility Contract, the Wholesale Price Flexibility Contract, the Commitment Contract and the Option Contract in order to achieve supply chain system coordinated, no matter analyzing from either the perspective of the manufacturer and wholesaler or the perspective of a multi-stage supply chain or multi-level one. With consumers’ “battle” intensified, relationship between supply chain members also began to develop from the original simple division of profit to mutual benefit and win-win results. The members can gain more profits only by improving the competitiveness of the entire supply chain, so it has become hot spots of researches that the relational contract is concerned about the relationship between supply chain members. Relational contract is a convention, more accurately, a trust that could not specified by stringent legal provisions. Therefore the commitment itself may be unlike the general traditional contract that can put into effect through a simple contract. Wang Yingjun [15] defined the relational contract: the relevant provisions that ensured buyers and sellers to coordinate and optimize the sales channel performance by providing the proper information and incentive measures. Baker [16] studied the interaction between clear contracts and subtle ones. Tunay I. Tunca [17] analyzed the difference and gained the interaction mechanism between the two kinds of contracts based on Baker’s research. Dyrer and Chu [18] indicated that Relational Contract could effectively reduce the possibility of supply chain members adopting opportunistic behavior, enhance mutual trust between the members, thereby improve information sharing and reduce asymmetric information by analyzing the drawbacks of opportunistic decision behavior. Sun Yuanxin and in Mao recommended [19] summarized the main features of relational contract, including embedded relation, self-compliance, long-term time, the openness of terms, and noted that the safeguards of Relational Contract implementation: value of future cooperation, reputation and relationship rules. In addition, existing researches will also be summarized as follows: Relational Contract as an alternative of formal ones, Governance of Relational Contract, the use of relational contract in incentives. There are more researches on Relational Contracts, such as Zhao Pinghan [20] , Li Ying [21] , Diana Yan Wu [22] , Spengler [23] , Kannan Govindan [24] and so on.
The commitment contract is a typical relational contract. Helper [25] , Dyers and Ouchi [26] , Helper and Sako [27] et al. compared business strategies between the local enterprises and foreign-funded ones in the study and found that the biggest difference was the different commitment quantity and information sharing amount. Obviously they both are related to the trust degree between each other. Studies have shown that the larger commitment quantity and information shared between supply chain members, the lower uncertainties and costs of the entire supply chain will be. Applying its conclusion to the real world, the manufacturer will reduce the number of wholesalers to some extent in order to increase its commitment amount for wholesalers as much as possible without exceeding its production capacity. On the other hand, the wholesaler will improve its degree of information sharing to exchange. Durango-Cohen and Yano [28] studied a commitment contract between ASIC manufacturers and customers, in which the manufacturer would commit a minimum supply quantity to a customer, when he provided a demand forecast and commit to buy some of them at least. Similar commitment contracts are also described in Tsay [29] , Tsay and Lovejoy [30] . Eppen and Iyer [31] have proposed a commitment contract on poor market, in which wholesalers have the right to pay only a part of its order quantity in advance when ordering and then choose to buy the remainder. Bassok [32] , Bassok and Anupindi [33] , Anupindi and Bassok [34] put forward some other commitment contracts in which the wholesalers updating the order quantity once again is allowed. Their application avoids the possibility of wholesalers exaggerating the market demand deliberately to a certain extent when sharing information and too low production of manufacturers.
Aiming to seasonal products with long production cycle, short sales period, unknown demand and large volatility, combining with the previous researches on the supply chain coordination with market demand information updates and based on the uncertainty theory, this paper further deepens and expands the application of commitment contract, which is a kind of relational contract, in the supply chain management. Based on the general newsboy model with uncertainty demand, this paper gives a two-stage supply chain model in case of market demand information updating and establishes the appropriate decision-making model from the perspective of the supply chain members (the manufacturer and the wholesaler) respectively, and then optimizes the corresponding supply chain contract with updating information from the two aspects.
Based on the lowest supply commitment contract, this paper establishes a two-stage three-stage supply chain system made up of a manufacturer and a wholesaler firstly: before the season beginning, the wholesaler and the manufacturer carry on the first time “blind” production and order. With the season coming, the wholesaler corrects the order quantity while he provides demand information with certain loyalty to the manufacturer. At the same time, the manufacturer of production revised inventory and promised the lowest supply. After the season beginning, the wholesaler can carry on replenishing once again according to the situation. Based on the supply chain above, this paper establishes the optimal decision model for the manufacturer and the wholesaler respectively and ultimately gets the wholesaler’s optimal order quantity, the value of the manufacturer’s optimal commitment, the optimal production quantity and other strategic decisions. Finally, it gives exponential analysis and obtains a more realistic conclusion.
2. Preliminary Model
2.1. Symbol Description
 : The market price of the commodity.
: The market price of the commodity.
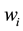 : The manufacturer’s wholesale price in the stage
: The manufacturer’s wholesale price in the stage 
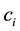 : Cost of the manufacturer’s production in the i-th stage.
: Cost of the manufacturer’s production in the i-th stage.
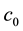 : Cost of implementation per unit of semi-finished products.
: Cost of implementation per unit of semi-finished products.
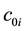 : The manufacturer’s cost of production per unit semi-finished in the stage.
: The manufacturer’s cost of production per unit semi-finished in the stage.
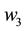 : Wholesaler’s replenishment wholesale price in the sales cycle.
: Wholesaler’s replenishment wholesale price in the sales cycle.
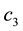 : Unit production cost when manufacturer start an emergency production in the sales season.
: Unit production cost when manufacturer start an emergency production in the sales season.
 : Total pre-season order quantity of wholesaler.
: Total pre-season order quantity of wholesaler.
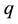 : Manufacturer’s total pre-season production inventory quantity.
: Manufacturer’s total pre-season production inventory quantity.
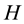 : Manufacturer’s total amount of pre-season semi-finished.
: Manufacturer’s total amount of pre-season semi-finished.
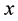 : Market demand, an uncertain variable
: Market demand, an uncertain variable 
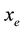 : The amount of market demand update
: The amount of market demand update 
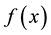 : Uncertain density function of the uncertain demand under normal state.
: Uncertain density function of the uncertain demand under normal state.
![]() : Uncertain distribution function of the uncertain demand under normal state.
: Uncertain distribution function of the uncertain demand under normal state.
![]() : Uncertain density function of market demand update.
: Uncertain density function of market demand update.
![]() : Uncertain distribution function of market demand update.
: Uncertain distribution function of market demand update.
2.2. Model Description
Definition 1 [Liu1]: The uncertainty distribution Φ of an uncertain variable ![]() is defined by
is defined by ![]() for any real number x.
for any real number x.
Definition 2 [Liu1]: An uncertain variable ![]() is called normal if it has a normal uncertainty distribution
is called normal if it has a normal uncertainty distribution
![]()
![]() . Denoted by
. Denoted by ![]() where e and σ are real numbers with
where e and σ are real numbers with![]() .
.
Definition 3 [Liu1]: Let ![]() be an uncertain variable. Then the expected value of
be an uncertain variable. Then the expected value of ![]() is defined by
is defined by
![]() (1)
(1)
provided that at least one of the two integrals is finite.
Theorem 1[Liu1]: Let ![]() be an uncertain variable with uncertainty distribution
be an uncertain variable with uncertainty distribution![]() . Then
. Then
![]() . (2)
. (2)
Based on the newsboy model, a production enterprise with unit production costs C, unit retail price P(P > C), D is stochastic market demand that policy makers facing. ![]() and
and ![]() are noted that uncertain distribution function and uncertain density function of the uncertain demand respectively. So the optimization model that makers use to choose the optimal inventory Q is
are noted that uncertain distribution function and uncertain density function of the uncertain demand respectively. So the optimization model that makers use to choose the optimal inventory Q is
![]() (3)
(3)
Calculating its derivative, we get
![]() (4)
(4)
![]() (5)
(5)
It means that ![]() is concave function of
is concave function of![]() . If we let the optimal inventory that makers chosed
. If we let the optimal inventory that makers chosed![]() , the final optimal profits of decision makers is
, the final optimal profits of decision makers is
![]() (6)
(6)
In the situation that information of market demand is uncertain and updating, as manufacturers can’t contact with the market, they get the updated information only through information sharing with wholesalers. Note ![]() as the market updates wholesalers get and
as the market updates wholesalers get and ![]() is that they provide to manufacturers, so we have
is that they provide to manufacturers, so we have![]() .
.
Phase 1: Manufacturers and wholesalers confirm uncertainty distribution of market demand with years of experience in sales and expert assessment, denoting as ![]() and
and ![]() respectively, and we have
respectively, and we have![]() . Wholesalers issued the first order to the manufacturer, in the order quantity is
. Wholesalers issued the first order to the manufacturer, in the order quantity is![]() . Manufacturers receive this order to determine the first time production
. Manufacturers receive this order to determine the first time production ![]() according to order quantity
according to order quantity![]() .
.
Phase 2: With the sales season approaching, wholesalers get the market updates![]() . They revises the order quantity
. They revises the order quantity ![]() according to
according to ![]() and
and![]() , and provide the sharing information
, and provide the sharing information ![]() to manufacturers at the same time. Manufacturers revise the production quantity
to manufacturers at the same time. Manufacturers revise the production quantity![]() , according to
, according to![]() , d and
, d and![]() . And as the permutation for information sharing, they provide the lowest estimated Quantity C. If the quantity that committed
. And as the permutation for information sharing, they provide the lowest estimated Quantity C. If the quantity that committed![]() , give producers punishment
, give producers punishment![]() , that is called loyalty punishment. Complementary, if manufacturers and wholesalers have cooperated for many years and have a good foundation of trust and loyalty, that is, manufacturers trust
, that is called loyalty punishment. Complementary, if manufacturers and wholesalers have cooperated for many years and have a good foundation of trust and loyalty, that is, manufacturers trust ![]() in a high level and wholesalers don’t exaggerate
in a high level and wholesalers don’t exaggerate ![]() (Difference between
(Difference between ![]() and
and ![]() is small.) and
is small.) and![]() .
.
Phase 3: With the sales season starting, we can get the market demand x, wholesalers selectively emit replenishment orders to manufacturers to resive the final order quantity according to the total order quantity d and demand x. As a manufacturer, they can only mechanically do their ability to distribute the surplus goods to wholesalers as complement goods. If the market needs are not met, give manufacturers and wholesalers s punishment considering loss from the customer, loss of reputation and so on. It is called shortage punishment.
Known from the above analysis, for a manufacturer, the quantity he committed must be greater than the wholesalers amount in the first two stages, that is,![]() . Taking 3 order opportunities into consideration, after the sales seasons beginning, the order quantity wholesalers expected is
. Taking 3 order opportunities into consideration, after the sales seasons beginning, the order quantity wholesalers expected is![]() . However, because of manufacturers’ limited production, the quantity is
. However, because of manufacturers’ limited production, the quantity is ![]() in fact. In addition, to be fair, shortage punishment of the contract allocates the responsibility in detail. Wholesalers shoulder the responsibility
in fact. In addition, to be fair, shortage punishment of the contract allocates the responsibility in detail. Wholesalers shoulder the responsibility
![]()
that caused by understanding updates insufficiently. That caused by limited production is ![]() which is assumed by manufacturers.
which is assumed by manufacturers.
Wholesalers take initiative relatively in the supply chain system and manufacturers make decisions due to the behavior of wholesalers. We assume that wholesalers know the manufacturers different responses to different![]() , although manufacturers do not know what market information
, although manufacturers do not know what market information ![]() wholesalers obtained is and how wholesalers choose
wholesalers obtained is and how wholesalers choose ![]() finally, in the context of asymmetric information. That is,
finally, in the context of asymmetric information. That is, ![]() is known for wholesalers.
is known for wholesalers.
2.3. The Optimization Model of Manufacturers Based on That Commitment Contract with Changing Demand Information
Known from a series of analysis above, we should set about from manufacturers. Obviously the order quantities were known in the two production decisions, so ![]() and
and![]() . The total profit of manufacturers is noted as
. The total profit of manufacturers is noted as![]() :
:
![]() (7)
(7)
It should be noted that manufacturers need not make any decisions in phase III, the producers do not need to make any decisions considering the collaboration process in the entire supply chain. Decomposing the expression by the stages of production decision and combining stage II and stage III, we can get the optimization model of manufacturer’s expected profits in this situation:
![]() (8)
(8)
In which, ![]()
![]() (9)
(9)
Analyzing the model above in the reverse order, we can analyze the decision problem in view of the stage II and solve ![]() from it. (Here
from it. (Here ![]() is abbreviated as the nesting issue on C and q.) Therefore, assuming that
is abbreviated as the nesting issue on C and q.) Therefore, assuming that ![]() is certain when solving, we analyze the optimal amount C committed.
is certain when solving, we analyze the optimal amount C committed.
Theorem 2: In the decision problem ![]() of stage II, the manufacturer optimum and minimum commitment supply quantity C is same with either the production or the amount of updating information. That is,
of stage II, the manufacturer optimum and minimum commitment supply quantity C is same with either the production or the amount of updating information. That is, ![]() or
or![]() .
.
Proof: reducing decision problem:
In the decision problem![]() , because
, because ![]() has nothing to do with C, we note it as K and get
has nothing to do with C, we note it as K and get
![]() . (10)
. (10)
Discussing different circumstances:
When![]() , that is
, that is![]() .
.
(i) When![]() , from
, from ![]() we can get that manufacturers do not need to bear shortage punishment. That is, the third term in the expression of
we can get that manufacturers do not need to bear shortage punishment. That is, the third term in the expression of ![]() is zero. So we have
is zero. So we have![]() . Obviously
. Obviously ![]() increases monotonously with committed amount C. So we have
increases monotonously with committed amount C. So we have![]() .
.
(ii) When![]() ,
,![]() . Known from nature of the condition
. Known from nature of the condition
uncertain distribution function,![]() . Therefore in order to maximize
. Therefore in order to maximize![]() , C should be taken at the endpoints:
, C should be taken at the endpoints: ![]() (
(![]() ) or
) or ![]() (
(![]() ).
).
(iii) When![]() , from
, from ![]() we can get that manufacturers do not need to bear loyalty punishment. That is,
we can get that manufacturers do not need to bear loyalty punishment. That is,
the second term in the expression of ![]() is zero. So we have
is zero. So we have![]() . In the same
. In the same
way, we take the derivative of C. Then we get
![]() (11)
(11)
That is, ![]() decreases monotonously with C, so
decreases monotonously with C, so![]() .
.
When![]() , we have
, we have![]() .
.
In this case, since the total production has exceeded the amount of updating information![]() , for manufacturers it is not necessary to increase the loyalty punishment. That is,
, for manufacturers it is not necessary to increase the loyalty punishment. That is, ![]() and the second term in the expression of
and the second term in the expression of ![]() is zero.
is zero.
(i) When![]() , manufacturers do not need to bear shortage punishment, so
, manufacturers do not need to bear shortage punishment, so ![]() is a constant about
is a constant about![]() . So
. So ![]() can take any value in the interval
can take any value in the interval![]() .
.
(ii) When![]() , it is same with (iii) of a) and we get
, it is same with (iii) of a) and we get![]() .
.
To sum up, the manufacturers’ the most optimal minimum commitment supply quantity satisfies ![]() or
or![]() .
.
Known from Theorem 2, the manufacturer will choose to avoid shortage punishment ![]() or loyalty punishment
or loyalty punishment![]() , when they decide their commitment supply quantity.
, when they decide their commitment supply quantity.
Based on these, we continue to analyze the optimal production capacity q.
Theorem 3: In the second stage of the decision problem![]() , the optimal production
, the optimal production ![]() that the manufacturer selected has the following expression
that the manufacturer selected has the following expression
![]() (12)
(12)
In which![]() , so we have
, so we have![]() ,
, ![]() or
or![]() . Here
. Here ![]() is decided by
is decided by![]() .
.
Proof: Compute the expectation of ![]() and we get
and we get
![]() (13)
(13)
Here ![]() is independent of C and q. Write it as L. So we obtain
is independent of C and q. Write it as L. So we obtain
![]() . (14)
. (14)
Discussing different circumstances:
When![]() , the manufacturer choosing to avoid shortage punishment, we have
, the manufacturer choosing to avoid shortage punishment, we have
![]() . (15)
. (15)
When![]() , we obtain
, we obtain
![]() (16)
(16)
From the nature of condition uncertain distributed function, we know![]() . Therefore, only let
. Therefore, only let ![]() in order to maximize
in order to maximize![]() . So that
. So that![]() .
.
When![]() , the manufacturer also choosing to avoid loyalty punishment, at this moment we have
, the manufacturer also choosing to avoid loyalty punishment, at this moment we have
![]() (17)
(17)
As
![]() (18)
(18)
So only let![]() , we can maximize
, we can maximize![]() . Thus we can determine the value of
. Thus we can determine the value of![]() . When
. When
![]() , the optimal strategy are
, the optimal strategy are ![]() and
and![]() .
.
When![]() , the manufacturer choosing to avoid loyalty punishment, at this time we have
, the manufacturer choosing to avoid loyalty punishment, at this time we have
![]() (19)
(19)
When![]() , as
, as![]() , we obtain
, we obtain ![]() or
or ![]() in order to maximize
in order to maximize![]() ;
;
When![]() , we get
, we get ![]() to maximize
to maximize![]() , at this time the production quantity is
, at this time the production quantity is![]() .
.
To sun up, the decision problem in the second stage has 4 possible optimal strategy, noting as
![]() .
.
Integrating above analysis, Theorem 2 and Theorem 3, at the beginning of stage II, the manufacturer obtain two decision programs for both strategies ![]() and
and ![]() with combining updating information
with combining updating information ![]() with the wholesaler’s total order quantity d. Finally, compare the two decisions to obtain the more optimal one. Here we must pay attention to the second revised total production q must satisfy
with the wholesaler’s total order quantity d. Finally, compare the two decisions to obtain the more optimal one. Here we must pay attention to the second revised total production q must satisfy![]() . We use
. We use ![]() instead of
instead of ![]() if the two decision program we choose don’t satisfy
if the two decision program we choose don’t satisfy![]() , and then compare them in the end.
, and then compare them in the end.
2.4. Optimization Model of Wholesalers with Demand Information Updates Based on the Commitment Contract
Relative to the manufacturers and wholesalers have been in a dominant position throughout the entire supply chain operation process. They take the initiate to carry on two pre-season orders, obtain the market information directly, selectively share it with the manufacturer, and understand the manufacturer’s response to update information. That is, they now how the manufacturer correct the demand distribution function ![]() according to updated information. Though further analysis, we can get
according to updated information. Though further analysis, we can get
![]() (20)
(20)
Here ![]() notes gross profit of the wholesaler and p notes the selling price. As a wholesaler, while having a larger initiative, but he has no room to make a decision in the third stage replenishment again and can only compensate the shortage possible mechanically. So explode the expression by the production phase, we get the following optimization model of wholesalers
notes gross profit of the wholesaler and p notes the selling price. As a wholesaler, while having a larger initiative, but he has no room to make a decision in the third stage replenishment again and can only compensate the shortage possible mechanically. So explode the expression by the production phase, we get the following optimization model of wholesalers
![]() , (21)
, (21)
in which![]() .
.
![]() (22)
(22)
Here ![]() notes the decision model of the wholesaler in the second phase, whose decision variables are the pre-season order quantity d and the sharing information
notes the decision model of the wholesaler in the second phase, whose decision variables are the pre-season order quantity d and the sharing information ![]() (
(![]() is obvious.), shorthand for
is obvious.), shorthand for![]() . Here it is emphasized that wholesalers fully understand manufacturers’ reaction and information. That is, the manufacturer’s decision variables
. Here it is emphasized that wholesalers fully understand manufacturers’ reaction and information. That is, the manufacturer’s decision variables ![]() and
and ![]() can be expected by the wholesaler while sharing the information and deciding the order quantity.
can be expected by the wholesaler while sharing the information and deciding the order quantity.
Theorem 4: In the second stage, the optimal pre-season order quantity that wholesalers selected is
![]() (23)
(23)
![]() (24)
(24)
Proof: Simplify the decision problem and get
![]() (25)
(25)
It is necessary to pay attention to that ![]() is related to d directly and explicitly, but generate indirect hidden relationship with
is related to d directly and explicitly, but generate indirect hidden relationship with ![]() by influencing C and q. Here we assume that wholesalers have the ability to find the completion in Theorem 2 and Theorem 3,
by influencing C and q. Here we assume that wholesalers have the ability to find the completion in Theorem 2 and Theorem 3, ![]() or
or![]() , through considering its strategy from the perspective of the manufacturer.
, through considering its strategy from the perspective of the manufacturer.
Discussing different circumstances:
When C = q,
(i) When q = d, we have
![]() (26)
(26)
(1) if![]() , we obtain,
, we obtain,
![]() (27)
(27)
Computing its derivation to d, we can get
![]() (28)
(28)
![]() . (29)
. (29)
In this case, ![]() is a Concave function on d. So at this moment wholesaler’s optimal order quantity is
is a Concave function on d. So at this moment wholesaler’s optimal order quantity is
if![]() , we obtain
, we obtain
![]() . (30)
. (30)
In this case, in order to maximize![]() , the more d is the better. So we get
, the more d is the better. So we get![]() .
.
(ii) When![]() , we have
, we have
![]() . (31)
. (31)
Here the second term and the fourth one are independent of d.
If![]() , we have
, we have
![]() (32)
(32)
And we can get further
![]() . (33)
. (33)
In the similar way, we obtain the optimal decision is![]() .
.
If![]() , we have
, we have
![]() . (34)
. (34)
At this moment, in order to maximize![]() , the more d is the better. So we get
, the more d is the better. So we get![]() .
.
b) When![]() ,
,
(i) When![]() , that the manufacturer’s decision policy is
, that the manufacturer’s decision policy is![]() , we have
, we have
![]() (35)
(35)
whose the last term is independent of d.
(1) if![]() , we obtain
, we obtain
![]() . (36)
. (36)
So we have ![]() and
and![]() . That is,
. That is, ![]() is a concave function on d in this case so at this moment we get
is a concave function on d in this case so at this moment we get ![]() is the optimal decision of the wholesaler.
is the optimal decision of the wholesaler.
(2) if![]() , we obtain
, we obtain
![]() (37)
(37)
At this moment, in order to maximize![]() , the more d is the better. So we get
, the more d is the better. So we get![]() .
.
(ii) When![]() , it is similar with case (ii) of a). So we have the optimal decision is
, it is similar with case (ii) of a). So we have the optimal decision is ![]()
or![]() .
.
Instruction: For a wholesaler, when choosing the optimal pre-season order quantity d from ![]() in the second stage, if d we want to chose doesn’t satisfy the pre-assumption
in the second stage, if d we want to chose doesn’t satisfy the pre-assumption![]() , we use
, we use ![]() to compare and chose the optimal decision instead of d.
to compare and chose the optimal decision instead of d.
2.5. Optimization Analysis of Supply Chain Based on the Commitment Contract with Information Updates
From the analysis in above part 2 and part 3, we get that in order to achieve coordination, supply chain should have the following conclusions, when the commitment amount C satisfy certain conditions.
Completion 1: Under the condition C = q, when![]() , the supply chain could achieve coordination in the case of q = d, while it could not achieve coordination in the case of
, the supply chain could achieve coordination in the case of q = d, while it could not achieve coordination in the case of![]() . On the other hand, when
. On the other hand, when![]() , the supply chain could achieve coordination in the case of q = d, while it could not achieve coordination in the case of
, the supply chain could achieve coordination in the case of q = d, while it could not achieve coordination in the case of![]() .
.
Proof: Under the condition C = q when![]() , the manufacturer’s optimal production quantity is
, the manufacturer’s optimal production quantity is ![]() or
or ![]() known from above part 2 and when q = d and
known from above part 2 and when q = d and![]() , the wholesaler’s optimal order quantity is
, the wholesaler’s optimal order quantity is ![]() (
(![]() ) known from above part 3. At this time to achieve coordination of supply chain, we
) known from above part 3. At this time to achieve coordination of supply chain, we
should have![]() . It need satisfy
. It need satisfy ![]() or
or![]() . What we need to do is only to adjust P.
. What we need to do is only to adjust P.
When q = d and![]() , the wholesaler’s optimal order quantity is
, the wholesaler’s optimal order quantity is ![]() (
(![]() ). We should have
). We should have ![]() to achieve coordination of supply chain. This condition can be achieved, so we can achieve supply chain coordination. In the case of
to achieve coordination of supply chain. This condition can be achieved, so we can achieve supply chain coordination. In the case of ![]() and
and![]() , the wholesaler’s optimal order quantity is dB (
, the wholesaler’s optimal order quantity is dB (![]() ). The wholesaler’s optimal order quantity is less than optimal production of the manufacturer, so they can not be equal. Therefore the supply chain coordination can not be achieved. Similarly, in the case of
). The wholesaler’s optimal order quantity is less than optimal production of the manufacturer, so they can not be equal. Therefore the supply chain coordination can not be achieved. Similarly, in the case of ![]() and
and![]() , the wholesaler’s optimal order quantity is d (
, the wholesaler’s optimal order quantity is d (![]() ). The wholesaler’s optimal order quantity is less than optimal production of the manufacturer, so they can not be equal. Therefore the supply chain coordination can not be achieved. QED
). The wholesaler’s optimal order quantity is less than optimal production of the manufacturer, so they can not be equal. Therefore the supply chain coordination can not be achieved. QED
Completion 2: Under the condition![]() , when
, when![]() , the supply chain could achieve coordination in the case of q = d, while it could not achieve coordination in the case of
, the supply chain could achieve coordination in the case of q = d, while it could not achieve coordination in the case of![]() . On the other hand, when
. On the other hand, when![]() , the supply chain could achieve coordination in the case of q = d, while it could not achieve coordination in the case of
, the supply chain could achieve coordination in the case of q = d, while it could not achieve coordination in the case of![]() .
.
Proof: Under the condition ![]() when
when![]() , the manufacturer’s optimal production quantity is
, the manufacturer’s optimal production quantity is![]() ,
, ![]() or
or ![]() known from above part 2 and when
known from above part 2 and when ![]() and
and![]() , the wholesaler’s optimal order quantity is
, the wholesaler’s optimal order quantity is ![]() (
(![]() ) known from above part 3. At this time to achieve coordination of supply
) known from above part 3. At this time to achieve coordination of supply
chain, we should have![]() . It need satisfy
. It need satisfy![]() ,
, ![]() or
or![]() . What we need to do is
. What we need to do is
only to adjust![]() . When q = d and
. When q = d and![]() , the wholesaler’s optimal order quantity is
, the wholesaler’s optimal order quantity is ![]() (
(![]() ). We should have
). We should have ![]() to achieve coordination of supply chain. This condition can be achieved, so we can achieve supply chain coordination. In the case of
to achieve coordination of supply chain. This condition can be achieved, so we can achieve supply chain coordination. In the case of ![]() and
and![]() , the wholesaler’s optimal order quantity is
, the wholesaler’s optimal order quantity is ![]() (
(![]() ). The wholesaler’s optimal order quantity is less than optimal production of the manufacturer, so they can not be equal. Therefore the supply chain coordination can not be achieved. Similarly, in the case of
). The wholesaler’s optimal order quantity is less than optimal production of the manufacturer, so they can not be equal. Therefore the supply chain coordination can not be achieved. Similarly, in the case of ![]() and
and![]() , the wholesaler’s optimal order quantity is d (
, the wholesaler’s optimal order quantity is d (![]() ). The wholesaler’s optimal order quantity is less than optimal production of the manufacturer, so they can not be equal. Therefore the supply chain coordination can not be achieved. QED
). The wholesaler’s optimal order quantity is less than optimal production of the manufacturer, so they can not be equal. Therefore the supply chain coordination can not be achieved. QED
Known from the above two completion and above analysis, when the manufacturer’s optimal production is larger than the wholesaler’s optimal order quantity, it is impossible to achieve optimal state of both of two members of the supply chain. Only one of them can be optimal, and the other will have some extra expense. In order to achieve the supply chain coordination, deduce more costs the other member paid from the more part of the profit the optimal member get than that without cooperation and the two members negotiate to allocate this part profits. Then the supply chain coordination can be achieved; when the manufacturer’s production is equal to the wholesaler’s order quantity, the supply chain coordination can be achieved. The two sides can reach optimal state under some conditions.
On the other hand, the total profits of the manufacturer is
![]() (37)
(37)
Computing the derivative of the above formula, at this time it is necessary that ![]() when
when ![]() and
and![]() , in order to reach the optimal expected profit of the whole supply chain.
, in order to reach the optimal expected profit of the whole supply chain.
This completion is to reach the optimal supply chain coordination in the case of q = d. It is similar with the process of get the optimal order quantity![]() .
.
3. Exponential Analysis
We assume that before market information updates, the manufacturer and wholesaler analyze and estimate that the market demand obey the normal uncertainty distribution![]() , in which
, in which![]() . Let p = 200,
. Let p = 200, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , s = 70, the wholesaler update the information with the market demand
, s = 70, the wholesaler update the information with the market demand![]() , which obey the uncertainty distribution
, which obey the uncertainty distribution![]() .
.
The wholesaler reflects to market information honestly. Here there is![]() .
.
As an manufacturer,![]() . In this case, the optimal production is
. In this case, the optimal production is ![]() or q* = qA = 64.61529. Corresponding optimal order quantity of the wholesaler is dA = 62.89546, dB = 61.48653, dC = 61.7073 and d = 60.
or q* = qA = 64.61529. Corresponding optimal order quantity of the wholesaler is dA = 62.89546, dB = 61.48653, dC = 61.7073 and d = 60.
The manufacturer gives a larger![]() . At this moment, we assume that
. At this moment, we assume that![]() .
.
As a manufacturer, ![]() whose uncertain mean is 60 and uncertain variance is 5. In this case, the optimal production is
whose uncertain mean is 60 and uncertain variance is 5. In this case, the optimal production is ![]() or
or![]() . Corresponding optimal order quantity of the wholesaler whose uncertain mean is 50 and uncertain variance is 5 is
. Corresponding optimal order quantity of the wholesaler whose uncertain mean is 50 and uncertain variance is 5 is![]() ,
, ![]() ,
, ![]() and d = 50. In this case, some costs of the manufacturer will increase, such as the product cost and shortage cost.
and d = 50. In this case, some costs of the manufacturer will increase, such as the product cost and shortage cost.
If the manufacturer does not consider new information the wholesaler provided, he still think![]() .
.
As a manufacturer, ![]() whose uncertain mean is 50 and uncertain variance is 5. In this case, the optimal production is
whose uncertain mean is 50 and uncertain variance is 5. In this case, the optimal production is ![]() or
or![]() . Corresponding the uncertain Distribution of the wholesaler’s optimal order quantity whose uncertain mean is 60 and uncertain variance is 5 is
. Corresponding the uncertain Distribution of the wholesaler’s optimal order quantity whose uncertain mean is 60 and uncertain variance is 5 is![]() ,
, ![]() ,
, ![]() and d = 60. In this case, some costs will be generated, such as shortage cost.
and d = 60. In this case, some costs will be generated, such as shortage cost.
Comparing the three cases above, we get the first one is the optimal and its cost is the lowest.
In addition, if complete the previous analyzed based on the probability theory, its result in the first case is as follows:
As a manufacturer,![]() . In this case, the optimal production is
. In this case, the optimal production is ![]() or q* = qA = 63.1682. Corresponding the wholesaler’s optimal order quantity (
or q* = qA = 63.1682. Corresponding the wholesaler’s optimal order quantity (![]() ) is dA = 59.7678, dB = 56.8318 and
) is dA = 59.7678, dB = 56.8318 and ![]() In this case, some costs will be generated, such as shortage cost.
In this case, some costs will be generated, such as shortage cost.
Compared with results obtained in the previous uncertainty theory, the optimal production value of the manufacturer’s is less slightly and the optimal value of wholesalers is less than the previous value.
The calculation is similar in the other two cases, so here we do not compare them.
4. Conclusion
Based on the uncertainty theory, this paper studies seasonal merchandise with long production cycle, relatively short marketing period, uncertain and strong volatile market demand. Setting about the perspective of market demand information updated, it analyzes the contract coordination problem of a two-stage three-stage supply chain system with a risk-neutral manufacturer and a risk-neutral wholesaler. In the system of pure contract supply chain, it cannot achieve coordination. It introduces the pledge contract, in the case that producers have twice pre-season production and wholesalers have twice pre-season order and a replenishment opportunity in the season. It established contract model respectively, and according to these models, it carried on the optimization analysis. The optimal quantity, the output of eugenics and the optimal amount of commitment of the supply chain members are presented. In the case of the wholesalers predomination, it gives the information sharing strategies that regulate the supply chain. In this paper, it is just an attempt to apply the uncertainty theory in supply chain. There may also be many problems, but after all, it has been applied to the practical problem. I believe it will be applied to analyze the supply chain system by more researchers.