1. Introduction
In the Standard Model, baryons are made of products from 3 quarks, selected from 3 pairs of quarks. Each pair is quarks with (2/3)e, and (−1/3)e fractional charges. These pairs are named (u, d) up and down quarks, (t, b) top and bottom quarks and (c, s) charm and strange quarks. According to the Projection-Gell-Mann Standard Model, there are however, only 3 fractional charged quarks generators, namely (u, t, d), where both u and t have charge of (2/3)e, while d has charge (−1/3)e, plus their antiparticles. These quarks form the SU(3) generators. (See Ref. [1] for the proof of Cartan identity.) Thus the (b, c, s) quarks cannot be fundamental SU(3) generators. In the gauge projection theory, the conformal projection requires the invariant parameter alpha = |q|/m(q) for the derivation of the fractional charge generators. Any violation of alpha will break the SU(3) symmetry. In the set of SU(3) generators, we have u and t, both with charge (2/3)e. Thus a new quantum signature must be introduced to distinguish between them. It is through this signature that we can construct from superpositions the (b, c, s) non-projection-gauge invariant quarks. With b = (u + d)*, s = (t + d)* and c = (s + d)*; such that mass m(b) = m(s) = m, and m(c) = (4/3)m, where m is the bare quark mass. Hence the α, the charge per unit quark mass invariance, required for the gauge transformation as shown in Ref. [1] is broken for b, c, s quarks.
Based on the above we define the proton as (uud) and the neutron as (udd). And since these two baryons only contain u and d quarks, their gluon potential is also generated by u and d intermediate quark currents. Hence the gluon potential U is generated by (uud) + (udd) + (ddd). As the gluon potential is a product of the 3 vector potentials generated from charge currents, the change of u and d by c, t and s, b will only modify through the perturbation correction on the potential energy which then depends on the mass change, which must be small. None the less no matter how small, it breaks the SU(3) symmetry. Lastly, this perturbative change of U, due to s, c, etc. will not change the baryon SU(3) representations as given by (1) × (8) × (8) × (10). Thus the missing heavy baryon octet contention [2] remains valid.
In the recent papers [3] - [6] we have shown how the meson masses are calculated, including the pion gluon potential pairs of intermediate quark currents, u or t and d. We explicitly obtained U(π) as 121 MeV. Similarly, the proton gluon U can also be calculated with the gauge loop parameter r0 already determined [4] [6] , and get U(p) = 934.6 MeV instead of the number fitting U(p) = 928 MeV we gave in Ref. [1] . It was also shown in ref. [4] - [6] that the inter quark interactions within hadrons are divided into 2 body for mesons and 3 body for baryons. The 3-body problem obeys the equilateral structure, meaning that all 3 pairs of relative distances are equal. And the reduced pair charges satisfy a net zero current rule. It was through these constructions that the proton, neutron masses were calculated, which agreed with data exactly. Gauge confinement restrictions for 2 and 3 quark states are given by flux quanta h/e only, while for 4, 5 and 6 quark states, due to possible reduction into lower unit e composites, there can be both quanta of h/e and 2h/e. As such there is a typo in the abstract of Ref. [6] . Namely π0 should be replaced by π+, in order the gauge loop radius is reduced by 1/2, needed for the binding between p and π+ to be 33.8 GeV.
It is one of our goals in this paper to investigate and calculate the rest of the known baryon masses [7] , and see if we can learn from it more properties of the Projection-Standard-Model that could shed light on the basic space-time curvature that can lead to the gravitational equation obtained through General Relativity [1] .
2. The Projection Violation on the Gluon Potential
As mentioned in the introduction the replacement of d quark by s quark in the baryon signature will result in the alpha invariant requirement of the conformal projection, so that the orthogonality between SU(2) × L and SU(3) × L is broken. Let us first review the proton, neutron states, where the Orthogonality holds. The signatures of proton is (uud), while that for the neutron is (udd), giving us the gluon potential proportional to:
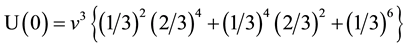 (2.1)
(2.1)
where v is the equal valued intermediate quark velocity.
Since the proton and neutron are only given by u and d quarks, there are no projection-gauge violations, and thus no perturbative correction to the vector potentials generated. Based on the determined gauge loop r0 from the mesons gluon potential, U0 is calculated equal to 934.6 MeV. The terms in Equation (2.1) can be divided into the sum of 21 equal values Eo, each then is of 44.5 MeV [4] . Accordingly, the mass level splitting in the proton, neutron octet would be 4 E0 roughly equal to 178 MeV, which is clearly in agreement with data. If no perturbative corrections are introduced due to u, d replacement by c, s, b, then the fine mass splitting are within each gluon level and completely due to the total inter quark energies from each baryon. As shown in Ref. [6] , we calculated the proton and neutron T.E., and got the masses as 938.4 MeV and 939.6 MeV respectively. However, many baryons signature contain c, s quarks, as shown by the signatures for Λ and Σ: s in the decuplet. Consider Λ0 and Σ0, these particles signatures are given as (udd) and (uds) respectively, and they also are within the same general gluon potential of 1112.6 MeV. Yet the Σ0 mass is heavier than that of Λ0 by nearly 80 MeV. In fact, Σ0 decays into Λ0 and emits photons. This is a clear indication, that their gluon potentials composed of vector potential fields only must be different due to s quark replacement for d quark in the intermediate states that generate the potential and must decay by photon emission.
It also means strangeness is not a conserved quantum. To show this quantitatively, let us start with the proton U(0). We obtain the next gluon level:
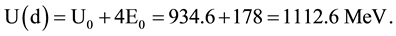 (2.2)
(2.2)
The total energy T.E. for Λ0 (udd),
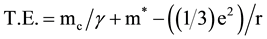 (2.3)
(2.3)
where the total mass mc = (4/3)m, and the reduced mass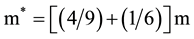 , γ = 0.486 and the potential values are determined in the same way as the neutron, as according to the 2D Chern-Simons relativistic ground state, the binding energy for −e2/r is that of the revolving mass m', and for this semion limit γ = 0.18 [5] [6] . Thus for the reduced potential
, γ = 0.486 and the potential values are determined in the same way as the neutron, as according to the 2D Chern-Simons relativistic ground state, the binding energy for −e2/r is that of the revolving mass m', and for this semion limit γ = 0.18 [5] [6] . Thus for the reduced potential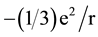 , the binding is (1/3) mc. And via orbital quantization we get γ = 0.486. Leading to T.E. = 86 MeV.
, the binding is (1/3) mc. And via orbital quantization we get γ = 0.486. Leading to T.E. = 86 MeV.
While the Σ0, is (uds), with mc = 2m, and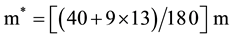 . Giving its
. Giving its
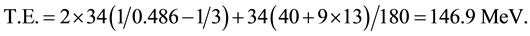
Should U(d) represent the gluon potential for Λ0, then it's mass is given by (see Ch. 8 of Ref. [1] for more details on the hadron mass formula)
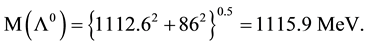 (2.4)
(2.4)
Although the T.E. for Σ0 is larger than that of Λ0, it is insufficient to produce a mass difference of nearly 80 MeV. In order that Σ0 is much heavier, U(d) must be replaced by U(s). By U(s), we mean one of the d quark in the intermediate states must be replaced by the s quark. Since all terms in U(d) involves at least one d quark. That means the correction due to such a replacement is linearly scaled.
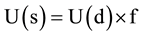 (2.5)
(2.5)
where f > 1, and is due to the perturbative energy correction caused by breaking of the α constant constrain required by P1, to obtain the SU(3) generators.
Should we assume
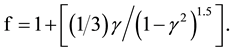 (2.6)
(2.6)
The factor (1/3) comes from the ratio of d mass to s mass. Using the Semion limit γ = 0.18, while the factor 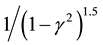 comes from cancelling the v3 dependence for the U correction, such that the effective corrective
comes from cancelling the v3 dependence for the U correction, such that the effective corrective
term m’ γ, where m’ represents the mass ratio modified as a result of the change in quark rest energy due to the replacement of the d quark by the s quark, remains and represents the spinor particle m’ reduced effective binding energy contribution. With the above, we get f = 1.063 and hence
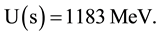 (2.7)
(2.7)
Finally, we get
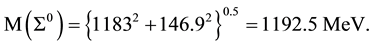 (2.8)
(2.8)
From this numerical calculation, we can conclude, that indeed the s quark when replacing d in the intermediate quark states will cause a SU(3) gluon potential symmetry breaking, and is likely also observed in other hadron masses.
3. The Inter Quark Potentials
With the gluon potential U(s) as given by Equation (2.7), we now proceed to calculate the T.E. for Σ+ = (uus). It is obvious that the net Coulomb potential is zero, and according to the net zero current rule for the pairs, in the trinity structure as discussed in Refs. [4] - [6] , we obtain
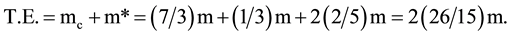 (3.1)
(3.1)
Thus
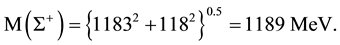 (3.2)
(3.2)
Similarly, Σ− = (dds), has a net repulsive Coulomb potential of (1/3)e2/r. And according to the net pair zero current rule for the trinity structure, it is static. Thus

Here we assumed that the value of the repulsive Coulomb potential can be approximated the same as that of the attractive potential giving the Chern-Simons Ground State [8] , except for the sign difference of binding energy change to repulsive energy.
This quantity is less than the T.E. of Σ0, which implies if Σ− is heavier, its U value must be larger. As we have shown the increase in U due to s replacement of d is a perturbative correction. The fact that Σ− signature is (dds), means s has 3! choices of replacing any one of the d quark. Making f modified to
![]() (3.3)
(3.3)
The factor (1/3)3 comes from the potential strength arising from the product of the (1/3)e charges giving U'(s) = 1188.9 MeV, and
![]() (3.4)
(3.4)
Moreover this extra U correction implies the SU(3) symmetry breaking of U can be a continuous probabilistic function of the alpha change in quark mass due to superposition. Our question is then: Is our fitting a purely numerical game or is the principle demonstrated in other baryons? In the Σ mass analysis, we were led by T.E. of each state being different because of their signatures. In the baryon decuplet, we have 4 Δ; (ddd), (ddu), (duu) and (uuu). None has s or c quark replacement, thus their T.E. are well defined and independent of the definition chosen for s and c. Irrespective of the U value, each T.E. can be computed with accuracy, and are of course different. Yet data shows their masses are close to the same. This can happen if U changes just so much as to cancel the change in T.E. in support of the U adjustment of Σ− from Σ0, while s, c substitutions in U are present, at least in small fractions.
The T.E. values of any of the Δ baryons are within 80 MeV and would only affect the resultant mass by![]() . Therefore any mass difference between them is very small even if U is the same for all of them. In fact U can be calculated U(s) + 44.5 = 1183 + 44.5 = 1227.5 MeV. The Δ mass is 1232 MeV, which certainly agrees with a T.E. of roughly 80 MeV. The 44.5 MeV U level addition comes from adding an intermediate state (ddd). Hence it is possible to replace one d in it by s, with different weight, allowing the adjustment of U slightly higher from Δ to Δ, such that all four Δ have the same mass of 1232 MeV and consistent in principle with the adjustment of U for Σ−.
. Therefore any mass difference between them is very small even if U is the same for all of them. In fact U can be calculated U(s) + 44.5 = 1183 + 44.5 = 1227.5 MeV. The Δ mass is 1232 MeV, which certainly agrees with a T.E. of roughly 80 MeV. The 44.5 MeV U level addition comes from adding an intermediate state (ddd). Hence it is possible to replace one d in it by s, with different weight, allowing the adjustment of U slightly higher from Δ to Δ, such that all four Δ have the same mass of 1232 MeV and consistent in principle with the adjustment of U for Σ−.
Another such an example of the U adjustment due to s replacement of d, is shown by Ξ−. The Ξ particles are given by (uss) and (dss). Here we have the signature replacement of two d quarks with two s quarks. Obviously, the U potential expressed in u,d,s, must be modified by a factor f, as follows:
![]() (3.5)
(3.5)
for f = 1.063 as given by Equation (2.6).
Again here the term 1, in the bracket in Equation (3.5) comes from the state (ddd), and thus can also be subjected to s replacement.
The net Coulomb potential for the (uss) Ξ0, is −(1/3)e2/r; while the Coulomb potential for (dss) Ξ−, is repulsive, and equal to (1/3)e2/r. Considering Ξ0, we have mc = 2.67m = 90.64 MeV and m* = 1.3m = 44.2 MeV. Thus its
![]() (3.6)
(3.6)
Taking U(Ξ0) as given by Equation (3.5), we obtain M(Ξ0) = 1319 MeV, which is in agreement with data [7] .
However the T.E. for Ξ− gives 139.8 MeV if we assume the same rule for the repulsive potential e2/r as equal to mc. This T.E. value is less than the T.E. of Ξ0, and therefore would need for further f correction, since Ξ− is heavier. The fact that the signature of Ξ− is (dss) implies that the last term in U(Ξ−) needs to be weighted higher, giving.
![]()
The last term in the bracket comes from the extra probability of replacing 2 d in d3 by s2.
Thus
![]() (3.7)
(3.7)
This serves as another example of U not being the same for both states, even though we have s in the U generation.
Lastly, we have Ω−, which is (sss). Hence according to our treatment of U(Ξ),
![]() (3.8)
(3.8)
with mc = 3m, m* = (3/2)m and![]() . Giving us a T.E. = 5.5m = 187 MeV.
. Giving us a T.E. = 5.5m = 187 MeV.
Finally
![]() (3.9)
(3.9)
Among the known baryons we have only one with c charm quark replacement for the u quark, which is Λ+, (ucd). U(c) is then generated by (ucd + 2cdd + ddd). The c quark is given by (s + d)*, thus its mass is (4/3)m. Like the proton, the Coulomb net V = 0, hence
![]() (3.10)
(3.10)
as T.E. value here compared to U(c) is unimportant.
The Λ+ mass is 2281 MeV meaning U(c) is close to 2275 MeV. This means U(c) must be scaled by f", such that![]() , where U(d) is generated by (uud + 2udd + ddd) the gluon potential for Λ0 which is 1112.6 MeV. While U(ddd) is 44.5 MeV.
, where U(d) is generated by (uud + 2udd + ddd) the gluon potential for Λ0 which is 1112.6 MeV. While U(ddd) is 44.5 MeV.
Suppose f" = 1 + f the increased factor 1 is because c actually is composed of 2 (1/3)e charge as compared to s, then
![]() (3.11)
(3.11)
Combining with T.E., we get
![]() (3.12)
(3.12)
This mass value is low compared to data. Thus there must be an error coming likely from f" approximation. By calculating backward, we get
![]() (3.13)
(3.13)
This increased value actually came from the mass ratio between u and c, which is![]() , instead of 1/3 for s replacement of d as given by Equation (2.6). Thus the perturbative factor f − 1 = 0.063, when replaced by f" it must be modified, due to the mass ratio change, when u is substituted by c, such that
, instead of 1/3 for s replacement of d as given by Equation (2.6). Thus the perturbative factor f − 1 = 0.063, when replaced by f" it must be modified, due to the mass ratio change, when u is substituted by c, such that
![]() (3.14)
(3.14)
Thus
![]() (3.15)
(3.15)
This number then give the Λ+ mass equal to 2284 MeV, a little high, but still in line with data.
On the whole the Projection-Standard-Model agrees very well with all data [7] .
4. Conclusions
This paper is not solely intended for showing how we can calculate the baryon masses from the Projection-Gell- Mann Standard Model. Although one might feel that the data fits could be artificially fixed. In reality, it is quite difficult, as the model started with the fixed U(0) proton gluon potential of 934.6 MeV plus the bare quark mass m of 34 MeV. For example, if we replace the signature of Λ0 from (udd) to (uds), there is no way to obtain its mass as compared to data to within 5 MeV which is beyond any experimental error bar. In fact it is not just difficult, but when they fit, the value is nearly precise to the decimal place of masses of baryons over 1000 MeV [4] [6] . In our recent papers [3] - [6] we showed how within same gluon potential levels, the inter quark Coulomb interactions produced the SU(3) mass splitting. This holds true for both mesons as well as baryons. For the mesons the inter quark interaction is a two-body problem, while for the baryons, it is a three-body problem. However, through the proton, neutron mass calculation, we discovered that for the three body space confined problem, in the baryon this confinement was gauge invariance. The leading solution is the trinity structure, or geometrically, the equilateral triangle, together with the net zero reduced pair current restriction [4] . In fact based on these rules, the calculated proton and neutron masses are precisely those of data. The equilateral triangle structure rule imposed on the baryons is vital to our ability to be able to calculate its T.E. as there is no iterative approximation that will work for the 3 body problem.
It was through these same procedures that we managed to calculate masses for all the known baryons shown in Section 3 above. In the process, we found that the 3 pairs of quarks, from the Standard Model, namely (u, d); (t, b) and (c, s), only (u, d, t) were the basic SU(3) generators as shown in Ref. [1] . The remaining three (b, c, s) are superpositions of (u, d, t) and violate the Projection-Gauge invariance. Because for the invariance the quantity α defined as |q|/m(q) must be a universal constant within the SU(3) × L manifold. We then found that b = (u + d)*, s = (t + d)*, while c = (s + d)*. Because of their respective masses making them all violate the α rule, it thus leads to the splitting of the gluon potential levels as they are substituted for any of the u, d, t quarks in the intermediate states that generate the gluon potential. It is then also obvious, because of the possible SU(3) × L continuous symmetry breaking, illustrated by the different baryons as shown from their masses, that the superposition of SU(2) × L and SU(3) × L can be made into a Riemannian Space-Time, as SU(2) and SU(3) are orthogonal groups. Giving us the general projection P = Po + P1, and the realization of a Riemannian space-time, where the curvature is dependent on the presence of mass, such that Perelman mappings [1] can be performed even in the quantum representation. It is this critical symmetry breaking via the gluon potentials that gives us General Relativity, and the gravitation field equation. But because in all hadrons, due to gauge confinement and the relativistic 2D Chern-Simons hydrogen ground state solution, it was shown that the gauge loop parameter must be inside the semion limit, thus making all hadrons as their statistic being fixed, therefore having a finite 4D space void, as represented by 3D × 1D, where the massless charged e-trino, anti-e-trino spinors and the repulsive gluon field generated by the quark currents in the enclosing boundary exist. This solution not only eliminated the singularity in the gravitational field solution, but also confirmed that the singularity was the result of the compacting of the 4th space dimension as suggested by Einstein [9] .