Asymptotic Behavior of Stochastic Strongly Damped Wave Equation with Multiplicative Noise ()
1. Introduction
Consider the following stochastic strongly damped wave equation with multiplicative noise:
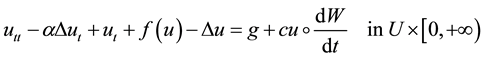 (1.1)
(1.1)
with the homogeneous Dirichlet boundary condition
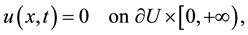 (1.2)
(1.2)
and the initial value conditions
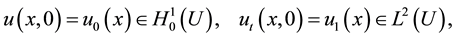 (1.3)
(1.3)
where 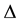 is the Laplacian with respect to the variable
is the Laplacian with respect to the variable ,
, 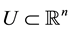 is a bounded open set with a smooth boundary
is a bounded open set with a smooth boundary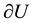 ;
; 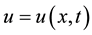 is a real function of
is a real function of 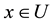 and
and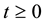 ;
; 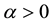
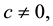 are strong damping coefficients;
are strong damping coefficients; 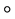 denotes the Stratonovich sense of the stochastic term;
denotes the Stratonovich sense of the stochastic term; 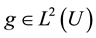 is a given external force;
is a given external force; ,
,  are uniformly bounded and there exist
are uniformly bounded and there exist ![]() such that
such that
![]() (1.4)
(1.4)
![]() (1.5)
(1.5)
where ![]() denotes the absolute value of number in
denotes the absolute value of number in![]() .
. ![]() is a one-dimensional two-sided real-valued Wiener process on probability space
is a one-dimensional two-sided real-valued Wiener process on probability space![]() , where
, where
![]()
the Borel ![]() -algebra
-algebra ![]() on
on ![]() is generated by the compact open topology, and
is generated by the compact open topology, and ![]() is the corresponding Wiener measure on
is the corresponding Wiener measure on![]() . We identify
. We identify ![]() with
with![]() , i.e.,
, i.e., ![]() When
When ![]() and
and ![]() Equation (1.1) can be regarded as a stochastic perturbed model of a continuous Josephson junction [1] , which is stochastic damped sine-Gordon equation [2] .
Equation (1.1) can be regarded as a stochastic perturbed model of a continuous Josephson junction [1] , which is stochastic damped sine-Gordon equation [2] .
A large amount of studies have been carried out toward the dynamics of a variety of systems related to Equation (1.1). For example, the asymptotical behavior of solutions for deterministic and stochastic wave equations has been studied by many authors, see, e.g. [3] - [27] and the references therein.
In this paper we study the existence of a global random attractor for stochastic strongly damped wave equations with multiplicative noise![]() . The coefficient
. The coefficient ![]() of the noise term needs to be suitable small,
of the noise term needs to be suitable small,
which is different from that in stochastic strongly damped wave equations with additive noise, this is because the multiplicative noise depends on the state variable ![]() but the additive noise term is independent of
but the additive noise term is independent of![]() .
.
This paper is organized as follows. In the next section, we recall some basic concepts and properties for general random dynamical systems. In Section 3, we provide some basic settings about Equation (1.1) and show that it generates a random dynamical system in proper function space. Section 4 is devoted to proving the existence of a unique random attractor of the random dynamical system.
2. Preliminaries
In this section, we collect some basic knowledge about general random dynamical systems (see [28] [29] for details).
Let ![]() be a separable Hilbert space with Borel
be a separable Hilbert space with Borel ![]() -algebra
-algebra![]() . Let
. Let ![]() be a probability space as in Section 1. Define
be a probability space as in Section 1. Define ![]() on
on ![]() via
via
![]()
then ![]() is an ergodic metric dynamical system [28] [29] .
is an ergodic metric dynamical system [28] [29] .
In the following, a property holds for ![]() -a.e.
-a.e. ![]() means that there is
means that there is ![]() with
with ![]() and
and ![]() for
for![]() .
.
Definition 2.1 A continuous random dynamical system on X over ![]() is a mapping
is a mapping
![]()
which is ![]() -measurable and satisfies, for
-measurable and satisfies, for ![]() -a.e.
-a.e.![]() ,
,
1) ![]() is the identity on
is the identity on![]() ;
;
2) ![]() for all
for all![]() ;
;
3) ![]() is continuous for all
is continuous for all![]() .
.
Definition 2.2 (See [29] ).
1) A set-valued mapping ![]() is said to be a random set if the mapping
is said to be a random set if the mapping ![]() is measurable for any
is measurable for any![]() . If
. If ![]() is also closed (compact) for each
is also closed (compact) for each![]() ,
, ![]()
is called a random closed (compact) set. A random set ![]() is said to be bounded if there exist
is said to be bounded if there exist ![]() and a random variable
and a random variable ![]() such that
such that
![]()
2) A random set ![]() is called tempered provided for
is called tempered provided for ![]() -a.e.
-a.e.![]() ,
,
![]()
3) A random set ![]() is said to be a random absorbing set if for any tempered random set
is said to be a random absorbing set if for any tempered random set![]() , and
, and ![]() -a.e.
-a.e.![]() , there exists
, there exists ![]() such that
such that
![]()
4) A random set ![]() is said to be a random attracting set if for any tempered random set
is said to be a random attracting set if for any tempered random set![]() , and
, and ![]() -a.e.
-a.e.![]() , we have
, we have
![]()
where ![]() is the Hausdorff semi-distance given by
is the Hausdorff semi-distance given by ![]() for any
for any![]() .
.
5) A random compact set ![]() is said to be a random attractor if it is a random attracting set and
is said to be a random attractor if it is a random attracting set and ![]() for
for ![]() -a.e.
-a.e. ![]() and all
and all![]() .
.
Theorem 2.3 (See [29] ). Let ![]() be a continuous random dynamical system on
be a continuous random dynamical system on ![]() over
over![]() . If there is a tempered random compact absorbing set
. If there is a tempered random compact absorbing set ![]() of
of![]() , then
, then ![]() is a compact random attractor of
is a compact random attractor of![]() , where
, where
![]()
Moreover, ![]() is the unique random attractor of
is the unique random attractor of![]() .
.
3. Stochastic Strongly Damped Wave Equation
In this section, we outline the basic setting of (1.1)-(1.2) and show that it generates a random dynamical system.
Define an unbounded operator
![]()
Clearly, ![]() is a self-adjoint, positive linear operator with the eigenvalues
is a self-adjoint, positive linear operator with the eigenvalues![]() :
:
![]()
It is well known that ![]() generates an analytic semigroup of bounded linear operators
generates an analytic semigroup of bounded linear operators ![]() on
on![]() .
.
Let![]() , endowed with the usual norm
, endowed with the usual norm
![]() (3.1)
(3.1)
where ![]() denotes the usual norm in
denotes the usual norm in ![]() and
and ![]() stands for the transposition.
stands for the transposition.
It is convenient to reduce (1.1) to an evolution equation of the first order in time
![]() (3.2)
(3.2)
For our purpose, it is convenient to convert the problems (1.1)-(1.2) into a deterministic system with a random parameter, and then show that it generates a random dynamical system.
We now introduce an Ornstein-Uhlenbeck process given by the Brownian motion. Put
![]() (3.3)
(3.3)
which is called Ornstein-Uhlenbeck process and solves the Itô equation
![]() (3.4)
(3.4)
From [30] [31] , it is known that the random variable ![]() is tempered, and there is a
is tempered, and there is a ![]() -invariant set
-invariant set ![]() of full
of full ![]() measure such that
measure such that ![]() is continuous in
is continuous in ![]() for every
for every![]() .
.
Lemma 3.1 (See [7] ). For the Ornstein-Uhlenbeck process ![]() in Equation (3.3), we have the following results
in Equation (3.3), we have the following results
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
![]() (3.7)
(3.7)
To show that problem (3.2) generates a random dynamical system, we let
![]()
which ![]() is a given positive number, then problems (1.1)-(1.2) can be rewritten as the equivalent system with random coefficients but without multiplicative noise on
is a given positive number, then problems (1.1)-(1.2) can be rewritten as the equivalent system with random coefficients but without multiplicative noise on![]() ,
,
![]() (3.8)
(3.8)
which has the following vector form
![]() (3.9)
(3.9)
where
![]()
![]()
We will consider Equation (3.8) or (3.9) for ![]() and write
and write ![]() as
as ![]() from now on.
from now on.
By the classical theory concerning the existence and uniqueness of the solutions [17] [32] , one may show that under conditions (1.4)-(1.5), for each![]() , problem (3.9) has a unique solution
, problem (3.9) has a unique solution ![]() which is continuous with respect to
which is continuous with respect to ![]() in
in ![]() for all
for all![]() . Then the solution mapping
. Then the solution mapping
![]() (3.10)
(3.10)
generates a continuous random dynamical system over ![]() on
on![]() .
.
Introduce the homeomorphism![]() , whose inverse homeomorphism is
, whose inverse homeomorphism is![]() ,
,![]() . Then the transformation
. Then the transformation
![]() (3.11)
(3.11)
also generates a continuous random dynamical system associated with the problem (3.2) on![]() .
.
Note that the two random dynamical systems ![]() and
and ![]() are equivalent. By transformation (3.11), it is easy to see that
are equivalent. By transformation (3.11), it is easy to see that ![]() has a random attractor provided
has a random attractor provided ![]() possesses a random attractor. Thus, we only need to consider the random dynamical system
possesses a random attractor. Thus, we only need to consider the random dynamical system![]() .
.
4. Random Attractor
In this section, we study the existence of a random attractor. Throughout this section we assume that ![]() is the collection of all tempered random subsets of
is the collection of all tempered random subsets of ![]() and
and
![]() (4.1)
(4.1)
For our purpose, we introduce a new norm ![]() by
by
![]() (4.2)
(4.2)
for![]() , where
, where ![]() and
and ![]() is chosen such that
is chosen such that ![]() in which
in which ![]() is a small positive number. It is easy to check that
is a small positive number. It is easy to check that ![]() is equivalent to the usual norm
is equivalent to the usual norm ![]() on
on ![]() in (3.1). For
in (3.1). For![]() ,
, ![]() , let
, let
![]() (4.3)
(4.3)
where ![]() denotes the inner product on
denotes the inner product on![]() . By the Poincaré inequality
. By the Poincaré inequality
![]() (4.4)
(4.4)
Equation (4.3) is then positive definite.
Now, we present a property of the operator ![]() in
in ![]() that plays an important role in this article.
that plays an important role in this article.
Lemma 4.1 Let![]() . There exists a small positive constant
. There exists a small positive constant ![]() such that for any
such that for any![]() ,
,
![]() (4.5)
(4.5)
The proof of Lemma 4.1 is similar to that of Lemma 1 in [24] . We hence omit it here.
Lemma 4.2 Assume that![]() , conditions (1.4), (1.5) and (4.1) hold. Then, there exists a random ball
, conditions (1.4), (1.5) and (4.1) hold. Then, there exists a random ball ![]() centered at 0 with random radius
centered at 0 with random radius ![]() such that for any
such that for any![]() , there is a
, there is a
![]() such that for any
such that for any ![]() satisfies for
satisfies for ![]() -a.e.
-a.e. ![]() and all
and all![]() ,
,
![]() (4.6)
(4.6)
Proof. Take the inner product ![]() of problem (3.9) with
of problem (3.9) with![]() . By the Cauchy-Schwartz inequality and the Young inequality, we find that
. By the Cauchy-Schwartz inequality and the Young inequality, we find that
![]()
![]()
![]()
![]()
![]()
where ![]() is the volume of the set
is the volume of the set![]() .
.
By using the Poincaré inequality (4.4), we have that
![]()
![]()
By all the above inequalities and Lemma 4.1, we have
![]() (4.7)
(4.7)
By the Gronwall lemma, we have that, for all![]() ,
,
![]() (4.8)
(4.8)
By replacing ![]() by
by![]() , we get from problem (4.8) that,
, we get from problem (4.8) that,
![]() (4.9)
(4.9)
By inequality (4.1), it is easy to see that
![]() (4.10)
(4.10)
It then follows from inequality (4.10), Lemma 3.1, ![]() and
and ![]() that
that
![]() (4.11)
(4.11)
By Lemma 3.1, inequality (4.10) and![]() , we have
, we have
![]() (4.12)
(4.12)
We choose
![]() (4.13)
(4.13)
Then, for any tempered random set![]() , there exists a
, there exists a ![]() such that for any
such that for any![]() , satisfies for
, satisfies for ![]() -a.e.
-a.e.![]() ,
, ![]() ,
,
![]() (4.14)
(4.14)
So, the proof is completed. ![]()
We now construct a random compact attracting set for RDS![]() . For this purpose, we decompose the solution
. For this purpose, we decompose the solution ![]() of Equation (3.9) with the initial value
of Equation (3.9) with the initial value ![]() into two parts
into two parts
![]() , satisfy, respectively
, satisfy, respectively
![]() (4.15)
(4.15)
![]() (4.16)
(4.16)
Lemma 4.3 Assume that![]() , conditions (1.4), (1.5) and (4.1) hold. Then, for any
, conditions (1.4), (1.5) and (4.1) hold. Then, for any![]() , and
, and![]() , we have for
, we have for ![]() -a.e.
-a.e.![]() ,
,
![]() (4.17)
(4.17)
and there exist a tempered random variable ![]() and
and ![]() such that for
such that for ![]() -a.e.
-a.e. ![]() and all
and all![]() ,
,
![]() (4.18)
(4.18)
where ![]() and
and ![]() satisfy Equations (4.15), (4.16).
satisfy Equations (4.15), (4.16).
Proof. We first take the inner product ![]() of Equation (4.15) with
of Equation (4.15) with![]() . By Lemma 4.1, we obtain
. By Lemma 4.1, we obtain
![]() (4.19)
(4.19)
Then by ![]() and
and![]() , we have
, we have
![]() (4.20)
(4.20)
Thus, the first assertion is valid.
Next, we take the inner product ![]() of Equation (4.16) with
of Equation (4.16) with![]() . From the positivity of the operator
. From the positivity of the operator![]() , we easily obtain
, we easily obtain
![]() (4.21)
(4.21)
By the Cauchy-Schwartz inequality and the Young inequality, we find that
![]()
![]()
![]()
![]()
![]()
By using inequality (4.4), we have that
![]()
![]()
Combining all the above inequalities and inequality (4.21), we have
![]() (4.22)
(4.22)
Using the Gronwall lemma, for all![]() , we get
, we get
![]() (4.23)
(4.23)
Replacing ![]() by
by ![]() we get from the above that,
we get from the above that,
![]() (4.24)
(4.24)
By Lemma 3.1, inequality (4.10) and![]() , we have
, we have
![]() (4.25)
(4.25)
We can choose
![]() (4.26)
(4.26)
then the second assertion is valid. ![]()
By Lemma 4.2 and Lemma 4.3, for any![]() ,
, ![]() ,
, ![]() , and for some constant
, and for some constant![]() , we have for
, we have for ![]() -a.e.
-a.e.![]() ,
,
![]() (4.27)
(4.27)
where![]() . Let
. Let ![]() be a closed ball of
be a closed ball of![]() :
:
![]() (4.28)
(4.28)
Then, by the compact embedding of ![]() into
into![]() ,
, ![]() is compact in
is compact in![]() .
.
Note that
![]() (4.29)
(4.29)
Then by Lemma 4.3 and inequality (4.27), we have for ![]() -a.e.
-a.e. ![]()
![]() (4.30)
(4.30)
which implies that ![]() is a random compact attracting set for
is a random compact attracting set for![]() . It follows from Equations (4.13) and (4.26) that
. It follows from Equations (4.13) and (4.26) that ![]() is tempered. Thus by Theorem 2.3, the main result of this section can now be stated as follows.
is tempered. Thus by Theorem 2.3, the main result of this section can now be stated as follows.
Theorem 4.4 Assume that![]() , conditions (1.4), (1.5) and (4.1) hold. Then, the random dynamical system
, conditions (1.4), (1.5) and (4.1) hold. Then, the random dynamical system ![]() has a unique compact random attractor
has a unique compact random attractor ![]() in
in![]() , where
, where
![]()
in which ![]() is a tempered random compact attracting set for
is a tempered random compact attracting set for![]() .
.
Supported
The authors are supported by National Natural Science Foundation of China (Nos. 11326114, 11401244, 11071165 and 11471290); Natural Science Research Project of Ordinary Universities in Jiangsu Province (No. 14KJB110003); the Foundation of Zhejiang Normal University (No. ZC304011068).