On the Interconnectedness of Schrodinger and Black-Scholes Equation ()
1. Introduction
In order to analyse and connect the two aforementioned equations, following facts will be presented [1] :
・ Schrodinger equation is the cornerstone of quantum mechanics while Black-Scholes equation is the cornerstone of quantitative economics. The following facts are to be used:
・ If we have a quantum particle, its position is a random variable; at the same time the price of security is a random variable.
・ The Schrodinger equation demands a complex state function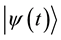 . At the same time, Black-Scholes is a real partial differential equation that always yields a real valued expression for the option price. Black- Scholes equation is like a Schrodinger equation for imaginary time.
. At the same time, Black-Scholes is a real partial differential equation that always yields a real valued expression for the option price. Black- Scholes equation is like a Schrodinger equation for imaginary time.
・ As Schrodinger equation demands a complex state function, the price of the option is analogous to the state function 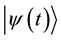 and the aforementioned state function requires a probabilistic interpretation. On the contrary, the option price
and the aforementioned state function requires a probabilistic interpretation. On the contrary, the option price 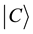 is directly observable and does not ask for probabilistic treatment.
is directly observable and does not ask for probabilistic treatment.
・ At the same time, in that sense referring to probabilistic interpretation above, Schrodinger equation has to
satisfy the following condition 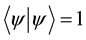 required by the probabilistic interpretation in quantum mechanics
required by the probabilistic interpretation in quantum mechanics
while at the same time the value of 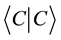 is arbitrary.
is arbitrary.
・ At the same time, we must refer to the Hamiltonians. All the Hamiltonians in quantum mechanics are Hermitian and therefore all eigenvalues are real. At the same time, Black-Scholes Hamiltonians that affect option price are not Hermitian and this causes eigenvalues that are complex.
・ Complex eigenvalues of Hamiltonians that are obtained in finance lead to a more complicated analysis than one encountered in quantum mechanics, in particular according to Belal E. Baaquie there is no well-defined procedure applicable to all Hamiltonians for choosing the set of functions that yield the completeness equation. The special cases where a similarity transformation leads to an equivalent Hermitian Hamiltonian yields a natural choice for the set of complete eigenfunctions.
・ Schrodinger equation is time reversible and is an initial value problem and time evolution is given by 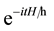 while Black-Scholes process is time irreversible due to its Hamiltonian being non-Hermitian and at the same time because pricing kernel is determined by the time-irreversible semi-group
while Black-Scholes process is time irreversible due to its Hamiltonian being non-Hermitian and at the same time because pricing kernel is determined by the time-irreversible semi-group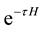 .
.
2. Theoretical Results
In order to analyse and see the similarity between Black-Scholes equation, it will be derived but in the formalism of quantum mechanics.
The Black-Scholes equation, but considering at the same time option price with constant volatility is given by:
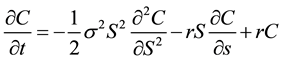 (1)
(1)
If the change of variable is implemented:
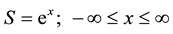 (2)
(2)
Then, the Black-Scholes-Schrodinger equation is obtained [1] .
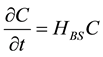 (3)
(3)
where the Black-Scholes Hamiltonian [2] is given by
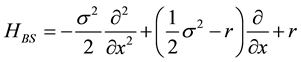 (4)
(4)
If we view the Black-Scholes as a quantum mechanical system, it only has one degree of freedom, x, with following analogies with Schrodinger equation:
・ Volatility-inverse of mass.
・ Drift term-(velocity-dependent) potential.
・ Price of the option C-Schrodinger state function.
In order to see if Black-Scholes Hamiltonian is Hermitian or anti-Hermitian, we must define and derive the following equations.
It is known that a matrix M has a Hermitian conjugate defined by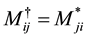 . The Hermitian conjugate on arbitrary operator O is given by [2] :
. The Hermitian conjugate on arbitrary operator O is given by [2] :
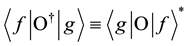 (5)
(5)
It is important to establish if Hamiltonian is Hermitian or anti-Hermitian because it is necessary to be aware of the space that an operator acts on, whether it acts on some N space or its dual space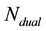 . The difference in finance is important.
. The difference in finance is important.
In order to analyse Black-Scholes and Schrodinger equation, the state space in quantum mechanics must be defined. It is important to explain completeness equation. Completeness equation refers to the existence of basis vector so that any arbitrary vector can be represented as a linear combination of these basis states [1] .
For all the application that will be examined, particle moves on a “continuous” line R; each point on the continuous line is a possible state for the system and thus the aforementioned particle requires continuously infinitely many independent basis vectors. However, the completeness equation of a two state is consequently to a N state system and then the limit of 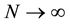 is taken.
is taken.
In order to introduce completeness equation, firstly we will introduce the example from the Belal E. Baaquie [1] . He is considering an electron moving in a space, its position is denoted by x and it can hop on the discrete points on a lattice, the points are given by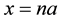 .
.
The basis states are labeled by ![]() and can be represented by an infinite column vector with the only non-zero entry being unity in the nth position. So we have the following:
and can be represented by an infinite column vector with the only non-zero entry being unity in the nth position. So we have the following:
![]()
![]() (6)
(6)
![]() (7)
(7)
![]() : completeness Equation (8)
: completeness Equation (8)
where ![]() above is the infinite-dimensional unit matrix. As we want the movement on lattice not to be discrete than continuous, we have to introduce the limit of
above is the infinite-dimensional unit matrix. As we want the movement on lattice not to be discrete than continuous, we have to introduce the limit of![]() . The state vector for the particle is given by the “ket” and its dual by the “bra” vector. This is where Hermitian of Hamiltonian plays the major role. Ket and bra vector are denoted respectively:
. The state vector for the particle is given by the “ket” and its dual by the “bra” vector. This is where Hermitian of Hamiltonian plays the major role. Ket and bra vector are denoted respectively:
![]() -“ket vector” and
-“ket vector” and ![]() -“bra vector”
-“bra vector”
In terms of the![]() , the following is defined:
, the following is defined:
![]() (9)
(9)
where the scalar product is given by Dirac delta function:
![]() (10)
(10)
The completeness equation is given by:
![]() -the completeness Equation (11)
-the completeness Equation (11)
where ![]() is the identity operator on (function) state space.
is the identity operator on (function) state space.
The presented completeness equation is a key equation in the analysis of the state space. For the case of two quantum particles with positions on x, y the completeness equation is given by:
![]() (12)
(12)
where![]() . If we want to generalize the completeness equation to many particles, the following equation is obtained for three particles.
. If we want to generalize the completeness equation to many particles, the following equation is obtained for three particles.
![]() (13)
(13)
where![]() . If we want to generalise the equation to n particles, the following result is obtained:
. If we want to generalise the equation to n particles, the following result is obtained:
![]() (14)
(14)
where ![]()
The two vectors represented by ![]() and
and ![]() can be mapped to each other. The aforementioned completeness equation gives the following:
can be mapped to each other. The aforementioned completeness equation gives the following:
![]() (15)
(15)
At the same time, according to completeness equation, we must derive the Hermitian adjoint between ![]() and
and
its adjoint operator![]() . The completeness equations presented above yield the following:
. The completeness equations presented above yield the following:
![]() (16)
(16)
The differential operator is anti_Hermitian. Now we will analyse the co-ordinate operator:
![]() (17)
(17)
The co-ordinate operator is Hermitian.
It was very important to introduce the following operators, as Hamiltonian operator, which is denoted by H, evolves the system in time and it is the most important operator in option pricing. The operator is non-Hermitian and is defined in the following.
We have introduced the co-ordinate operator and differential operator. As Belal E. Baaquie [2] points out there are special eigenstates that are of particular importance for all operators. For the co-ordinate operator, equation can be written as:
![]() (18)
(18)
This vector is called an eigenstate of the co-ordinate operator ![]() with real eigenvalue x since
with real eigenvalue x since ![]() is Hermitian.
is Hermitian.
According to Belal E. Baaquie, the eigenvalue equation for a non-Hermitian Hamiltonian H is given by a generalization of the the equation and the following equation. There exists special quantum states which are called energy eigenstates with real energy eigenvalues that form a complete set of states and are given by:
![]() (19)
(19)
By using the above equation, we obtain the following equations for eigenvalues and eigenfunctions:
![]() (20)
(20)
The density of states for eigenvalue E is defined by, marked as![]() :
:
![]() (21)
(21)
The completeness equation is:
![]() (22)
(22)
Hamiltonian operator is an operator ![]()
On the other side, if we want to write down the Schrodinger equation, we first need to specify the degrees of freedom of the system and at the same time it is necessary to specify the Hamiltonian H of the system that describes the range of energy as well as form of energy the system can have.
The celebrated Schrodinger equation is given by
![]() (23)
(23)
At the same time, we will be considering the quantum particle with m moving in one dimension in potential![]() , the Schrodinger equation is given:
, the Schrodinger equation is given:
![]() (24)
(24)
where the Hamiltonian operator acts on dual basis.
The Hamiltonian for the quantum particle moving in one dimension is given by:
![]() (25)
(25)
If we now compare Schrodinger Hamiltonian and Black-Scholes Hamiltonian, we can conclude the following:
![]() -Schrodinger Hamiltonian (26)
-Schrodinger Hamiltonian (26)
![]() -Black-Scholes Hamiltonian (27)
-Black-Scholes Hamiltonian (27)
Schrodinger potential ![]() is equal to
is equal to ![]() and
and
Schrodinger ![]() is equal to
is equal to![]() .
.
After having demonstrated the similarity between Black-Scholes Hamiltonian and Schrodinger Hamiltonian, it can be proved that that the price of the option satisfies the (imaginary time) Schrodinger equation [3] :
![]() (28)
(28)
with the final value fixed by the payoff function as follows:
![]() (29)
(29)
Comparing the wave function of quantum mechanics, the option price ![]() is directly observable, at the same time there is no concept of quantum measurement in option theory. The similarity of option pricing with quantum mechanics, at this stage, is mathematical:
is directly observable, at the same time there is no concept of quantum measurement in option theory. The similarity of option pricing with quantum mechanics, at this stage, is mathematical:
They can be described by an infinite-dimensional linear vector space ![]() and linear operators like H acting on vector space.
and linear operators like H acting on vector space.
At the same time, we must assume that Hamiltonian has the following general form [2] :
![]() (30)
(30)
where ![]() is an arbitrary function of x. It is the volatility of stock price and indicates the degree to which the evolution of stock price is random.
is an arbitrary function of x. It is the volatility of stock price and indicates the degree to which the evolution of stock price is random.
The famous Black-Scholes Hamiltonian ![]() is not Hermitian and it was derived above. It is important to be aware that this is the property of all the Hamiltonians in finance.
is not Hermitian and it was derived above. It is important to be aware that this is the property of all the Hamiltonians in finance.
By having presented Hamiltonians, we would like to give the final Black-Scholes Schrodinger equation [4] :
![]() (31)
(31)
In terms of the variable ![]() and time t, the Black-Scholes-Schrodinger equation for option pricing is given by [5] :
and time t, the Black-Scholes-Schrodinger equation for option pricing is given by [5] :
![]() (32)
(32)
It was proved that by using Schrodinger equation and Black-Scholes Hamiltonian, the famous Black-Scholes equation can be derived. It appears in this form since variable S is the variable of choice in the most literature in finance. This represents the basics of quantum social science [5] .
3. Conclusion
After having presented the main differences between Schrodinger equation which is a cornerstone of quantum physics and Black-Scholes equation which is the cornerstone of quantitative finance, it is proved that Black- Scholes equation can be derived from Schrodinger equation by using tools of quantum mechanics. The aforementioned approach paves the way towards further bonding of quantum physics and finance, creating in that way quantum finance which could become a powerful tool in asset pricing in the coming years.