Choice of an Advanced Rheological Model for Modeling the Viscoelastic Behavior of Hot Mixtures Asphalt (HMA) from Sénégal (West Africa) ()
1. Introduction
Asphalt concretes behavior is linear viscoelastic to low deformations and low cycles of loading [1] . This behavior is intermediate between the behavior of a perfect elastic solid and that of a Newtonian liquid [2] . In a linear viscoelastic behavior, the material properties are assumed independents of the applied stress or strain levels. The analysis of the linear viscoelastic behavior is done either by using the rheological models, or complex modulus, or creep compliance. These three methods are linked. In fact the conversion from creep compliance to the mechanical model is possible by the method of successive residuals, and the change from the complex modulus to creep compliance by the Fourier transforms [2] . The complex modulus E* is defined as a complex number that links stress to strain for a linear viscoelastic material subjected to a sinusoidal loading [3] . The absolute value of the complex modulus is commonly referred to as the “dynamic” modulus |E*| [4] . The phase angle 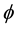 characterizes the deviation between stress and strain of a viscoelastic material. The |E*| is an approximation of the elastic modulus of a viscoelastic material, which can be used for pavement design when the laws of elasticity are employed. When the laws of viscoelasticity are applied, the mechanical models are used. In pavement design, the asphalt concrete layer can be considered as elastic or viscoelastic materials. The MEPDG [5] and the Alizé- LCPC software’s [6] consider asphalt concretes as elastic materials, characterized by dynamic modulus and Poisson ratio. Software which uses viscoelastic behavior needs to calibrate viscoelastic analogic model like the Huet, the Huet-Sayegh and the 2S2P1D models by complex modulus laboratory test results. In this study these models will be calibrated with results from complex modulus test (LC 26-700) performed with six asphalt concretes. The goodness of fit is measured statistically by the least squares method through the “Sum of Squared Deviation” (SSD).
characterizes the deviation between stress and strain of a viscoelastic material. The |E*| is an approximation of the elastic modulus of a viscoelastic material, which can be used for pavement design when the laws of elasticity are employed. When the laws of viscoelasticity are applied, the mechanical models are used. In pavement design, the asphalt concrete layer can be considered as elastic or viscoelastic materials. The MEPDG [5] and the Alizé- LCPC software’s [6] consider asphalt concretes as elastic materials, characterized by dynamic modulus and Poisson ratio. Software which uses viscoelastic behavior needs to calibrate viscoelastic analogic model like the Huet, the Huet-Sayegh and the 2S2P1D models by complex modulus laboratory test results. In this study these models will be calibrated with results from complex modulus test (LC 26-700) performed with six asphalt concretes. The goodness of fit is measured statistically by the least squares method through the “Sum of Squared Deviation” (SSD).
2. Methodology
2.1. The Advanced Viscoelastic Rheological Models
Figure 1 shows the first advanced viscoelastic model. That model is the Huet model [7] . These components are one spring and one dashpot connected in series. The Huet model is characterized by an infinite number of kelvin Voigt models in series or Maxwell models in parallel. His spectrum is continuous.
The express of complex modulus E* by the Huet model is done by Equation (1).
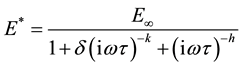 (1)
(1)
with (i) the complex number defined by i2 = -1 ; ω = 2π frequency, pulsation; E∞: limit of the complex modulus when ωτ → ∞; h, k: exponents such that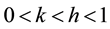 ; δ: dimensionless constant; τ: time characteristic whose value varies only with temperature. Huet model is limited at high temperatures and low frequencies because it has not a static modulus E0.
; δ: dimensionless constant; τ: time characteristic whose value varies only with temperature. Huet model is limited at high temperatures and low frequencies because it has not a static modulus E0.
Huet-Sayegh model solve this problem by added a spring in parallel to Huet model [8] . The spring represents
the static modulus [9] (Figure 2). Equation (2) shows the express of complex modulus by the Huet-Sayegh model.
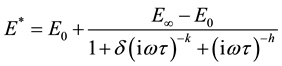 (2)
(2)
with (i) the complex number defined by i2 = -1; ω = 2π frequency, pulsation; E∞: limit the complex modulus when ωτ → ∞; E0 the static modulus of spring; h, k: exponents such that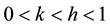 ; δ: dimensionless constant; τ: time characteristic whose value varies only with temperature. As Huet model, Huet-Sayegh model is characterized by a continuous spectral.
; δ: dimensionless constant; τ: time characteristic whose value varies only with temperature. As Huet model, Huet-Sayegh model is characterized by a continuous spectral.
Di Benedetto and colleagues [10] developed the 2S2P1D model. The model is obtained by added a linear dashpot in series to Huet-Sayegh model (Figure 3). The 2S2P1D model improves the Huet-Sayegh model at high temperatures and low frequencies [9] .
Equation (3) shows the express of complex modulus by the 2S2P1D model.
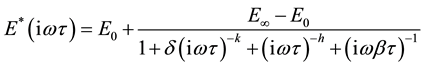 (3)
(3)
where (i) is the complex number defined by i2 = -1; *ω = 2π frequency pulse; k, h are exponents such that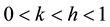 ; E0 (“static module”) when the module ωτ → 0; E∞ (“glassy modulus”) when the module ωτ → ∞; τ: time characteristic, whose value depends only on the temperature; β: dimensionless constant; η: viscosity Newtonian;
; E0 (“static module”) when the module ωτ → 0; E∞ (“glassy modulus”) when the module ωτ → ∞; τ: time characteristic, whose value depends only on the temperature; β: dimensionless constant; η: viscosity Newtonian;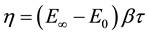 . When ωτ → 0, then
. When ωτ → 0, then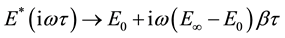 .
.
2.2. Complex Modulus Test and Results Visualization
The complex modulus test is used to measure the dynamic modulus |E*| of asphalt concrete named “Hot Mixture Asphalt” (HMA) at different temperatures and loading frequencies. The test can be conducted in a uniaxial or triaxial condition in either compression or tension. However, the majority of tests during the past years were in compression [12] . When the test is conducted in compression, the specimen experiences creep, in addition to the dynamic response. In the analysis of results, the creep response is typically ignored and the dynamic modulus is taken as the ratio of the amplitude of the dynamic stress to the amplitude of the dynamic strain. The tension/ compression test on cylindrical specimen belongs to the homogeneous tests, i.e. it makes it possible to obtain directly the linear viscoelastic behavior through the complex modulus. The principle of this test consists in soli- citing in traction and compression a cylindrical specimen in a continuous way according to a sinusoidal signal (traction/compression) centered on zero and applied according to the axial direction of the specimen. In the case of a complex modulus test, a low number of cycles are applied to various frequencies [13] . Complex modulus tests were performed using the Direct Traction-Compression (DTC) test on cylindrical samples according to Canadian and European standards (LC 26-700 and NF EN 12697-26, respectively). Six mixtures (Table 1) were studied (BDC, BDD BDF, GDC, GDD and GDF). Each formula undergoes measurements at temperatures of 0˚C, 10˚C, 20˚C, 30˚C, 40˚C and 55˚C and for each temperature the frequencies are 10 Hz, 5 Hz, 1 Hz, 0.3 Hz
![]()
Table 1. Components of asphalt concrete studied.
and 0.1 Hz. The apparatus used is a MTS Press imposing a strain of 50 μ def. During the test a 4 hours conditioning time is observed for each change in temperature so that it is homogeneous in the sample. The temperature changes are applied from the lowest to the highest. For each temperature, the stress is applied for different target frequencies from the highest to lowest with a limited number of cycles.
2.3. Test Results
Visco-analyse is a LCPC (actual IFSTAR) software developed by Emmanuel Chailleux in 2007 [11] .
It is used to visualize the results of complex modulus test for asphalt concretes and bituminous binders, to build master curve and finally to calibrate the advanced viscoelastic models (Huet, Huet-Sayegh and 2S2P1D). Inputs are the dynamic modulus |E*| and phase angle measured in several temperatures and frequencies for each temperature. In this part, the complex modulus test results on studied mixtures (BDD, BDC, BDF, GDD, GDC et GDF) are visualized on Visco-analyse. Table 2, present the normalized files input for Visco-analyse Software. In fact two input files are proposed in this software. The first is specific to results of METRAVIB viscoelas- timeter. The second use an ascii normalized file as presented in Table 2.
![]()
Table 2. List of two normalized file inputs for Visco-analyse software.
In the first columns we find the temperatures number, the frequencies number. Data are then rows in temperatures blocks. For each line we find successively, temperature, frequency, dynamic modulus and phase angle. The units are ˚C, Hz, Pa and degree.
First time results are visualized in Cole and Cole plane and in Black Space. After the verification of the uniqueness of Cole and Cole and Black Diagrams, the master curve can be drawn by application of the time- temperature superposition principle. The reference temperature of master curve is 10˚C. Figure 4 shows the uniqueness of Cole and Cole diagram for all mixtures studied.
Figure 5 shows a unicity of Black diagram for all mixtures studied.
The uniqueness of all Cole and Cole and Black diagrams showed above proof that de asphalt concrete studied are thermorheologically simples. And a master curve can be drawn by application of time-temperature superpo- sition principle.
![]()
Figure 4. E* Cole and Cole diagrams for BDC, GDC, BDD, GDD, BDF and GDF.
![]()
Figure 5. E* Black diagrams for BDC, GDC, BDD, GDD, BDF and GDF.
Figure 6 shows the master curves at the reference temperatures (0˚C, 10˚C, 20˚C, 30˚C, 40˚C and 55˚C) for
BDC mixture. Note that the master curve of a reference temperature to the other the master curve obtained at a given reference temperature, is only a translation of the master curve of other reference temperatures. Translation of master curve between temperatures is carried by the “William Landel Ferry” (W.L.F). or Arrhenius law [1] .
2.4. Calibration of Viscoelastic Advanced Model
After the visualization of complex modulus test results, the proposed viscoelastic models by the software (without modified Huet model) are calibrated. The calibration is a fitting process of dynamic modulus and phase angle. Model parameters are performed by fitting the master curve of complex modulus test results (Cole and Cole and Black Diagrams). First time all parameters are calculated at a reference temperature (10˚C). Models are transposed to the others temperature by using the “Willian Landel and Ferry” law (WLF) on the time parameter![]() . The minimization of prediction error is expressed by the sum of squared deviation (SSD) [11] .
. The minimization of prediction error is expressed by the sum of squared deviation (SSD) [11] .
Two algorithms are proposed in the Visco-analyse software, the “gradient” and the “simplex”.
The method “gradient” permits from close game parameters of a solution to quickly reach fine convergence. This algorithm called “trust-region reflective Newton” also gives access to the confidence interval on specified parameters. The second is the “simplex” method that searches a set of very distant from the initial data set parameters, while avoiding getting negative parameters [11] .
In this study the two algorithms are used successively. A first “gradient” optimization is performed. Then the Black curves and Cole and Cole are checked. Then, a second optimization is performed on the “simplex” by ensuring that the curves obtained are not worse than the first and only negative parameters have not been determined. This method significantly reduces the SSD. The final step of the calibration is the calibration of the coefficients A0, A1 and A2. As WLF, these coefficients are used to translate the model to other temperatures by Equation (4).
![]() (4)
(4)
Où:
![]() = decreasing function of temperature, which reflects the principle of time-temperature equivalence;
= decreasing function of temperature, which reflects the principle of time-temperature equivalence;
A0, A1 and A2 = the regression coefficients;
X = temperature sometime noted![]() .
.
3. Statistical Analysis and Interpretations of Calibration Results
The method of least squares is a statistical method analysis, independently developed by Gauss and Legendre.
![]()
Figure 6. Master curves at reference temperature (0˚C, 10˚C, 20˚C, 30˚C, 40˚C and 55˚C) for BDC.
Method is used to compare the experimental data, usually tainted by measurement errors with a mathematical model meant to describe these data [14] . In our case the models studied are complex functions predicting the complex modulus of asphalt concretes (Huet model, Huet-Sayegh model and 2S2P1D model).
The method consists of a prescription (initially empirical) which is the function ![]() which describes “best” data is the one that minimizes the quadratic sum of the deviations of measurements with the predictions of
which describes “best” data is the one that minimizes the quadratic sum of the deviations of measurements with the predictions of![]() . For example, if we have N measurements, (yi) i = 1, N the “optimal” parameters θ within the meaning of the least squares method are those which minimize the quantity [14] :
. For example, if we have N measurements, (yi) i = 1, N the “optimal” parameters θ within the meaning of the least squares method are those which minimize the quantity [14] :
where ri(θ) are the residues to the model, i.e. the differences between the measurement points (yi) and the model (x; θ).
S(θ) or (SSD) presented in Equation (5) can be considered as a measure of the distance between the experi- mental data and the theoretical model that predicts such data. Prescription least squares command that this dis- tance is minimal [14] .
![]() (5)
(5)
After the good uniqueness of master curves shows by Figure 4 and Figure 5 before, the viscoelastic models were calibrated. The dense-fine mixture (BDF and GDF) shows some irregularity of measures. As complex modulus and creep compliance, the viscoelastic models can characterize the behavior of viscoelastic materials. Among these models the advanced viscoelastic models are the most used in rational French pavement design. The calibration results in Table 3 show that the Huet the Huet-Sayegh and the 2S2D1P models are very performance in the prediction of complex modulus and the modeling of master curves. In fact the average prediction error for each model is relatively constant around SSD = 0.185. The best precision is obtained by the 2S2P1D model with a value of 0.169. Figure 7 shows results of fitting obtained, but some irregularities is observed with the 2S2P1D
![]()
Figure 7. (a) Modeling of complex modulus E* Cole and Cole diagram by Huet Model (exemple GDC mix); (b) Modeling of complex modulus E* Black diagram by Huet Model (exemple BDC mix); (c) Modeling of complex modulus E* Cole and Cole diagram by 2S2P1D Model (BDC mix); (d) Modeling of complex modulus E* Black diagram by 2S2P1D Model (BDC mix).
![]()
Table 3. Calibration parameters of advanced rheological models.
model linked to the imperfection of the software used (simplex gradient).
François Olard in 2004 [10] . stipulate that the value of static modulus E0 of Huet Sayegh model was probably linked to aggregates skeleton. The Static modulus presented in Table 3 shows a superior value for BDC (in Huet and Huet-Sayegh models) and relatively constant for others mixtures. Conclusion about this observation is that the static modulus E0 can be impacted by the aggregate skeleton, but this impact is visible for high difference between aggregate mixtures.
4. Conclusion
In the way of model choice for asphalt concrete mixed with basalt of Diack and quartzite of Bakel, the Huet and the Huet-Sayegh and 2S2P1D models are all representatives for modeling the viscoelastic behavior of asphalt concrete mixed with basalt of Diack and quartzite of Bakel. In fact they all have a low sum of squared deviation (SSD) minimized around 0.185. The best value of 0.169, obtained by the 2S2P1D model with the BDC mixture can suppose that it is the best model representing the viscoelastic behavior of asphalt concrete mixed with aggregate of Senegal. But some irregularities are observed in the fitting of Cole and Cole diagrams by the 2S2P1D model. These irregularities are definitely linked to the software.
Acknowledgements
The authors would like to acknowledge Professor Meissa FALL (RIP) for his guidance and valuable input in this research project; and the “Mapathé NDIOUCK Enterprise” for supporting the high price shipping of aggregates from Senegal to Canada.