Welfare Improvement and the Extension of the Income Gap under Monopoly ()
1. Introduction
Economics traditionally considers a monopoly to be bad for an economy. The most famous research indicating that monopolies are bad is the classical partial equilibrium analysis performed by Hicks [1] . This research indicates that a monopoly lowers the total surplus, and thus, the economy with a monopoly is not Pareto efficient. The result of this research is summerized in most of the textbook in microeconomics, e.g. Varian (1992), Okuno (2008) or Mas-Colell, Whinston, and Green (1995) [2] -[4] .
This research focuses on monopoly from a fresh perspective. The traditional monopoly model includes two characters: the monopolistic firm and the consumer. However, a real monopolistic situation necessarily involves a third character, namely, the investor. Under capitalism, investors are also consumers. Therefore, in our model, consumers invest in the monopolistic firm, which distributes its profit into its investors.
We formalize the above circumstance in a model, and analyze its model. We find that the total surplus of an economy may improve under a monopoly, which contradicts the traditional rationale for monopolies being bad. Meanwhile, in such a case the income gap often is expanded by market trade. If the initial income gap is sufficiently large, then a monopoly exacerbates this expansion of the income gap. The reason for this is as follows. Consider there are two consumers, where one is poor and another is rich. Both consumers invest in a firm that sells their own products and transfers its margin to investors in the form of dividends. However, the poor consumer has only limited ability to invest, and thus receives only a small share of the margin on product sales. The bulk of the margin is expropriated by the rich consumer. In this scenario, monopoly exacerbates this expansion of the income gap by enlarging firm’s profit.
This is the case in which the initial income gap is very high. In the case where the initial income gap is not so high, under certain assumptions monopoly also exacerbate the expansion of the income gap. Although these assumptions are not clear in the theoretical sense, we believe that these assumptions are intuitively natural.
In Section 2, we introduce our model and show the results. Section 3 is the conclusion.
2. The Model
We construct two models, named model 1 and model 2, to compare the competitive case with the monopolistic case. Model 1 corresponds with the competitive case, while model 2 corresponds with the monopolistic case. Both models consist of two consumers and one firm. Both consumers have a utility function , where
, where
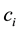 denotes private consumption and denotes the amount of money. We assume that
denotes private consumption and denotes the amount of money. We assume that 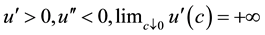 , and
, and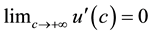 . In the beginning of the model, consumer
. In the beginning of the model, consumer  has
has 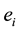 units of money and one unit of labor. Without loss of generality, we assume
units of money and one unit of labor. Without loss of generality, we assume . In the first-stage of the model, consumer
. In the first-stage of the model, consumer  determines the amount of investment
determines the amount of investment 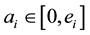 at same time. Then the stock ratio
at same time. Then the stock ratio 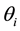 is defined as
is defined as 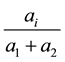 and the capital of the firm
and the capital of the firm 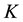 is defined as
is defined as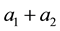 . The product function of the firm is denoted as
. The product function of the firm is denoted as . We assume that
. We assume that 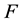 is homogeneous of degree one,
is homogeneous of degree one, 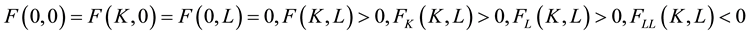 for all
for all![]() , and
, and ![]() and
and ![]() for all
for all![]() .
.
The second-stage is different from each model. In model 1, each consumer and firm participates in the competitive market and the equilibrium arises. In model 2, the firm determines the price of consumption ![]() monopolistically and the wage
monopolistically and the wage ![]() is determined competitively1.
is determined competitively1.
2.1. The First Model
First, we solve the second-stage. The first-order condition of consumer ![]() is,
is,
![]()
![]()
Hence,
![]()
and thus, ![]() in equilibrium. Meanwhile, the equilibrium condition of this market is
in equilibrium. Meanwhile, the equilibrium condition of this market is
![]()
and,
![]()
Hence, the equilibrium price is
![]()
Next, the first-order condition of the firm is,
![]()
Thus, the equilibrium wage is
![]()
Then, the profit of firm is2
![]()
where the subscript 1 represents that it is the profit of the first model. Hence, ![]() is positive, and the average profit
is positive, and the average profit ![]() is decreasing.
is decreasing.
Therefore, the payoff function of this model ![]() is3,
is3,
![]()
In the first-stage, consumer ![]() chooses
chooses ![]() simultaneously and the Nash equilibrium arises.
simultaneously and the Nash equilibrium arises.
Define
![]()
and ![]() as the unique solution of
as the unique solution of![]() . Then,
. Then,
![]() (1)
(1)
Hence, ![]() and thus
and thus ![]() if and only if
if and only if ![]() Note that K* is the social optimal level of capital, since
Note that K* is the social optimal level of capital, since ![]() for any
for any ![]() and thus
and thus ![]()
We show the following proposition:
Proposition 1: There exists a Nash equilibrium![]() . If
. If ![]() then
then ![]() is the unique Nash equilibrium. If not, then for any Nash equilibrium
is the unique Nash equilibrium. If not, then for any Nash equilibrium![]() ,
, ![]() and
and![]() , and thus,
, and thus,![]() .
.
Proof: We first suppose![]() . We can easily verify that
. We can easily verify that ![]() is not a Nash equilibrium. Note that
is not a Nash equilibrium. Note that ![]() is always negative since
is always negative since ![]() is decreasing. By Equation (1), 1) if
is decreasing. By Equation (1), 1) if ![]() and
and![]() , then
, then ![]() and
and![]() , which implies that
, which implies that ![]() is not a Nash equilibrium; 2) if
is not a Nash equilibrium; 2) if![]() $ and
$ and![]() , then
, then ![]() and
and![]() , which implies that
, which implies that ![]() is not a Nash equilibrium; 3) if
is not a Nash equilibrium; 3) if ![]() and
and![]() , then
, then ![]() and
and![]() , which implies that
, which implies that ![]() is not a Nash equilibrium. Hence, there is no Nash equilibrium other than
is not a Nash equilibrium. Hence, there is no Nash equilibrium other than![]() .
.
To show that ![]() is in fact a Nash equilibrium, consider the function
is in fact a Nash equilibrium, consider the function![]() . By Equation (1),
. By Equation (1), ![]() if
if ![]() and
and ![]() if
if![]() . Thus,
. Thus, ![]() is the best response to
is the best response to![]() . Likewise, we can show that
. Likewise, we can show that ![]() is the best response to
is the best response to![]() . This completes the proof of this case.
. This completes the proof of this case.
Next, suppose![]() . It can easily be verified that there is no Nash equilibrium such that
. It can easily be verified that there is no Nash equilibrium such that![]() . Next, since the function
. Next, since the function ![]() is continuous on
is continuous on![]() , there uniquely exists
, there uniquely exists ![]() which attains maximum. If
which attains maximum. If![]() , then
, then ![]() and thus
and thus![]() , a contradiction. Hence,
, a contradiction. Hence,![]() . Also, if
. Also, if![]() , then
, then ![]() and
and![]() , a contradiction. Hence,
, a contradiction. Hence,![]() . Therefore,
. Therefore, ![]() and thus
and thus ![]() $, which implies
$, which implies ![]() is a Nash equilibrium. This completes the proof.
is a Nash equilibrium. This completes the proof.
2.2. The Second Model
The demand function of consumer ![]() on private consumption is simply
on private consumption is simply
![]()
Hence, the total demand is![]() . Thus, to sell
. Thus, to sell![]() , the firm must choose
, the firm must choose![]() . Then, the profit function is
. Then, the profit function is
![]()
Now, we introduce an assumption.
ASSUMPTION 1: For any![]() , there exists
, there exists ![]() such that
such that ![]() is a maximum point of
is a maximum point of![]() .
.
By first-order condition, we have
![]()
Recall that ![]() is the unique value such that
is the unique value such that![]() . Thus, in equilibrium, the profit of the firm is
. Thus, in equilibrium, the profit of the firm is
![]()
Then, the payoff function of this model ![]() is
is
![]()
We want to focus on the case where the equilibrium of the first stage is well-defined. Therefore, we introduce an additional assumption:
ASSUMPTION 2: ![]() is decreasing in
is decreasing in![]() .
.
Here, we provide a sufficient condition of ASSUMPTION 2 to show this assumption is not too strong.
Proposition 2: Suppose that ASSUMPTION 1 holds. Then, ASSUMPTION 2 holds if ![]() is decreasing in
is decreasing in![]() .
.
Proof: By ASSUMPTION 1 and the second-order necessary condition, we have
![]()
Meanwhile, since ![]() is decreasing, we have
is decreasing, we have
![]()
By homogeneity of degree one on![]() ,
,
![]()
Further, both ![]() and
and ![]() are homogeneous of degree zero4. Therefore,
are homogeneous of degree zero4. Therefore,
![]()
and thus,
![]()
Hence,
![]()
and thus, ASSUMPTION 2 holds. This completes the proof.
It can be easily verified that ![]() is decreasing for any u that has constant or decreasing relative risk aversion. Hence, ASSUMPTION 2 is not too strong5.
is decreasing for any u that has constant or decreasing relative risk aversion. Hence, ASSUMPTION 2 is not too strong5.
Define
![]()
and ![]() as the unique solution of
as the unique solution of![]() . If such
. If such ![]() does not exist, then let
does not exist, then let ![]() Then,
Then, ![]() and thus
and thus ![]() if and only if
if and only if![]() . Note that
. Note that ![]() is well-defined under ASSUMPTION 2. Since
is well-defined under ASSUMPTION 2. Since ![]() for all
for all![]() , we have
, we have![]() .
.
We will show the following proposition:
Proposition 3: Under ASSUMPTIONS 1-2, there exists a Nash equilibrium![]() . If
. If![]() , then
, then ![]() is the unique Nash equilibrium. If not, then for any Nash equilibrium
is the unique Nash equilibrium. If not, then for any Nash equilibrium![]() ,
, ![]() and
and![]() .
.
Proof: It can be verified in the same way as Proposition 1.
2.3. Example: Improvement of Total Welfare
Suppose ![]() and
and![]() . By easy calculation, we have in model 1,
. By easy calculation, we have in model 1,
![]()
and thus,
![]()
Therefore, we have
![]()
![]()
![]()
In model 2, we have
![]()
and thus,
![]()
Therefore,
![]()
![]()
![]()
This example demonstrates that the existence of the case where monopoly improves the total surplus.
2.4. Comparative Statics
First, we argue the following result.
Proposition 4: Suppose that ![]() is sufficiently low. Define
is sufficiently low. Define
![]() .
.
Then, we have ![]() for any Nash equilibria
for any Nash equilibria ![]() of model 1 and
of model 1 and ![]() of model 2 with
of model 2 with![]() .
.
Proof: It suffices to show that our claim holds if![]() , because this model is continuous on parameter
, because this model is continuous on parameter![]() . Thus, we assume
. Thus, we assume![]() . By calculation in subsection 2.2, we have
. By calculation in subsection 2.2, we have![]() , and thus
, and thus ![]() for any
for any![]() . Hence, we can easily verify that
. Hence, we can easily verify that![]() , and thus
, and thus
![]()
which completes the proof.
Later, 2) of Proposition 5 says that under ASSUMPTION 3, the restriction of proposition 4 is removed. Here we introduce additional assumptions.
ASSUMPTION 3: ![]() is increasing in
is increasing in![]() .
.
ASSUMPTION 4: ![]() is increasing in
is increasing in![]() .
.
Remark: ASSUMPTIONS 3-4 are not clear in the theoretical view. However, we think both conditions are natural in the real world. Usually, the bigger the capital obtained, the richer the firm becomes. Also, if the monopolistic power of the firm becomes strong, then we can expect wages to decrease. Note that by definition,![]() is always positive.
is always positive.
Proposition 5: Suppose ASSUMPTIONS 1-2 hold, and choose any Nash equilibria ![]() of model 1 and
of model 1 and ![]() of model 2. Then,
of model 2. Then,
1) ![]() if
if![]() ;
;
2) Under ASSUMPTION 3, ![]() if
if![]() , and
, and ![]() if
if![]() ;
;
3) Under ASSUMPTIONS 3-4, ![]() and
and![]() . Further,
. Further, ![]() if
if ![]() and
and![]() .
.
Proof: If![]() , then
, then ![]() and 1) holds.
and 1) holds.
Suppose ASSUMPTION 3 holds. By easy calculation,
![]()
and thus,
![]()
Recall that![]() . By ASSUMPTION 2,
. By ASSUMPTION 2, ![]() is a decreasing function, and thus
is a decreasing function, and thus ![]() for any
for any![]() . Thus, we have
. Thus, we have
![]()
Since ![]() and
and ![]() is decreasing, we have
is decreasing, we have![]() , and thus,
, and thus,
![]()
Note that ![]() if
if ![]() and
and ![]() if
if![]() . Hence, for any
. Hence, for any ![]() such that
such that ![]() and
and![]() ,
,![]() .
.
If![]() , then
, then![]() . Hence,
. Hence, ![]() and if
and if![]() , then the inequality is strict. If not, then
, then the inequality is strict. If not, then![]() , and thus
, and thus ![]() since
since ![]() for any
for any![]() . Thus, (2) holds.
. Thus, (2) holds.
Lastly, suppose ASSUMPTIONS 3-4 hold. If![]() , then (1) and (2) imply (3). Otherwise,
, then (1) and (2) imply (3). Otherwise, ![]() and
and![]() . Now,
. Now,
![]()
whenever![]() . Hence, for any
. Hence, for any![]() ,
,
![]()
and thus,![]() . If
. If![]() , then
, then
![]()
and thus,![]() . Thus, 3) holds.
. Thus, 3) holds.
3. Conclusion
We constructed a model of a monopoly with investors, and showed that monopoly did not necessarily decrease total welfare. Meanwhile, under mild assumptions monopoly exacerbated the expansion of the income gap. Therefore, we revealed a new aspect of the negative influence of monopoly.
Acknowledgements
We are grateful for Eisei Ohtaki for his comments and suggestions.
Notes
1In the second-stage, we assume that the consumption space of each consumer is ![]() . This assumption is made for tha sake of simplicity and is not essential. We note that this setup is introduced in the explanation of the quasi-linear preference in Mas-Colell, Whinston and Green (1995).
. This assumption is made for tha sake of simplicity and is not essential. We note that this setup is introduced in the explanation of the quasi-linear preference in Mas-Colell, Whinston and Green (1995).
![]()
2Use the Euler equation ![]()
3If![]() , then no production arises and
, then no production arises and![]() . But we can easily verify that such situation is not a Nash equilibrium, since
. But we can easily verify that such situation is not a Nash equilibrium, since ![]() is positive.
is positive.
![]()
4For example, to differentiate ![]() with respect to
with respect to![]() , we have
, we have ![]() and thus
and thus![]() .
.
5Actually, we think that there may exist a weaker condition than ASSUMPTION 2 ensuring the following Propositions. However, since ASSUMPTION 2 itself is not too strong, we satiate this assumption, at least in this paper.