Low Density Instability in Asymmetric Nuclear Matter Using Pion Dressing ()
1. Introduction
The characteristics of dense nuclear matter are very much interesting for particle physics, astrophysics, as well as nuclear physics [1] -[7] . The nuclear equation of state, especially its stability, is an important item for the study of dynamic evolution of the early Universe, the stability of the neutron stars and the pattern of change of nuclear matter properties below the saturation density. Nuclear matter is predicted to exhibit phase transition between Fermi liquid and nucleonic gas at saturation density and elevated temperature. Analysis of nuclear multifragmentation [8] supports the idea that the mixed phase of neutron and proton matter may be formed [9] -[11] . Since these nuclei are made of neutrons and protons, the nuclear liquid-gas phase transition is a binary system where one has to deal with two independent proton and neutron chemical potentials for baryon number and charge conservation. There are experiments showing that the formation of highly excited compound nuclei in equilibrium is interpreted as the two coexisting phases of liquid and gas in the frame work of hydrodynamics. The liquid-gas phase transition is also useful for the study of core of compact stars in the range of the densities from ρ = 0.03 fm−3 to saturation density ρ0 = 0.15 fm−3. It is observed that the phase transition leads to an isospin distillation phenomenon [8] (isospin content of each phase is different). In fact, the information coming from the experiments with heavy ions in intermediate and high energy collisions [8] shows that the equation of state (EOS) depends not only on the energy beam but also sensibly on the proton fraction . The symmetry-energy, which describes the single nucleonic energy or nuclear matter changes as one, replaces protons with neutrons in the system. It determines the birth of neutron stars and supernova neutrinos and also plays the crucial role in the evolution of core collapse of supernovae.
. The symmetry-energy, which describes the single nucleonic energy or nuclear matter changes as one, replaces protons with neutrons in the system. It determines the birth of neutron stars and supernova neutrinos and also plays the crucial role in the evolution of core collapse of supernovae.
Understanding of the properties of the hot nuclear matter at normal and low density regions is of crucial importance for explaining the stability and structure of nutron stars after the supernova explosion. The experiments with unstable nuclear beams and relativistic heavy ions are the potential tools in determining the best equation of state (EOS) which may be derived from either relativistic or potential model. The problem of dense nuclear matter therefore has been a hot bed of investigations for the past few years and was looked by Walecka [12] , and others [13] [14] known as the Non Linear Walecka Model (NLWM). They consider the nucleon-neutral scalar field interactions with σ and ω in a nonperturbative method, treating these scalar fields as elementary. They reproduce correct bulk modulus of dense nuclear matter [15] . However, several open questions still remain unanswered. One of the basic questions is the microscopic nature of σ-field which is unclear in Walecka model since σ cannot be interpreted as the physical particle as it has not been discovered. Secondly, one cannot have the nonrelativistic limit of the model in a straight forward way. Since the points are playing a crucial role in neutron matter in terms of pion-nucleon interaction, it is the essential ingredient for studying such neutron stars. It is worth mentioning here that pion-nucleon interaction was a basic ingredient to study the nuclear processes [16] in the past with pion as elementary particle, and might play a crucial role in nucleon matter in terms of pion-nucleon interaction and enhance the nuclear matter properties. The  model with further inclusion of mesons like π, ρ etc. [14] [17] was taken to study its properties. Being motivated, we try to study and understand the stability and the symmetry energy of nuclear matter with pion dressing [18] in the present work. In fact it is known that the introduction of σ and ρ mesons in the constant coupling model leads to stability of the nuclear matter which is not oblivious for density-dependent models.
model with further inclusion of mesons like π, ρ etc. [14] [17] was taken to study its properties. Being motivated, we try to study and understand the stability and the symmetry energy of nuclear matter with pion dressing [18] in the present work. In fact it is known that the introduction of σ and ρ mesons in the constant coupling model leads to stability of the nuclear matter which is not oblivious for density-dependent models.
The article is organized as follows. In Section 2, we review the formalism of asymmetric dense nuclear matter taking nonrelativistic pion nucleon interaction and determine the symmetry energy Esym, symmetry energy slope L and curvature parameter of symmetry energy Ksym and their effects on stability of nuclear matter. In Section 3, we study the stability condition using stability matrix eigen vectors dependence on densities. In Section 4, we analyze our results which agree with other works [19] in this field.
2. Formalism
We consider the effective Hamiltonian for pion nucleon interaction [18] and [20] [21] as
 (1)
(1)
where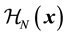 ,
, 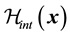 and
and  are the Hamiltonians for the free nucleon part, the pion-interaction part and the free meson part respectively. Here
are the Hamiltonians for the free nucleon part, the pion-interaction part and the free meson part respectively. Here 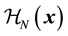 is given by
is given by
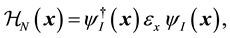 (2)
(2)
and the effective Hamiltonian  for pion nucleon
for pion nucleon 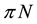 interaction part [22] is given by
interaction part [22] is given by
 (3)
(3)
We have taken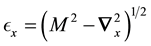 , with M as the mass of the nucleon. The free meson part of the Hamiltonian is given by
, with M as the mass of the nucleon. The free meson part of the Hamiltonian is given by
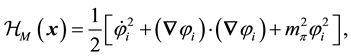 (4)
(4)
where 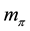 denotes the mass of the meson and
denotes the mass of the meson and . The pion field expansion in Equation (4) in terms of annihilation and creation operators is given by
. The pion field expansion in Equation (4) in terms of annihilation and creation operators is given by
 (5)
(5)
with![]() .
.
The two pions constitute a scalar-isoscalar interaction of nucleons and thus could simulate the effects of σ- mesons. The bare nucleon states however can get dressed with pions. These states are necessary for the correct description of nuclear matter. We now proceed to introduce a “meson” dressing of nuclear matter through the state [18]
![]() (6)
(6)
where the two pion creation operator ![]() is constructed with the creation and annihilation operators in momentum space as
is constructed with the creation and annihilation operators in momentum space as
![]() (7)
(7)
and the free nucleon energy density becomes
![]() (8)
(8)
where the spin degeneracy factor ![]() for proton and neutron. The density ρ and the Fermi momentum
for proton and neutron. The density ρ and the Fermi momentum ![]() are related by the equation
are related by the equation
![]() (9)
(9)
With the meson field operator expansion as in Equation (5) we may write Equation (4) as
![]() (10)
(10)
Using Equation (10), we now obtain kinetic energy density due to the mesons as
![]() (11)
(11)
where![]() . We next proceed to evaluate from Equation (3) which is the interaction energy density, with
. We next proceed to evaluate from Equation (3) which is the interaction energy density, with![]() ,
,
![]() (12)
(12)
In the non-relativistic limit and using Equation (7), the kinatic energy density (12) becomes
![]() (13)
(13)
The meson energy density thus is given as
![]() (14)
(14)
Now extremising Equation (14) with respect to![]() , we obtain the solution
, we obtain the solution
![]() (15)
(15)
where ![]() are the densities of nuclear matter, neutron matter and proton matter respectively. We note that Equation (15) is not acceptable since the energy density diverges. This happens because we have taken the pions to be point like and assumed that they can approach as near each other as they like which is physically not correct. If we bring two pions close to each other, there will be an effective force of repulsion because of their composite structure. We thus assume a phenomenological term corresponding to meson repulsion as
are the densities of nuclear matter, neutron matter and proton matter respectively. We note that Equation (15) is not acceptable since the energy density diverges. This happens because we have taken the pions to be point like and assumed that they can approach as near each other as they like which is physically not correct. If we bring two pions close to each other, there will be an effective force of repulsion because of their composite structure. We thus assume a phenomenological term corresponding to meson repulsion as
![]() (16)
(16)
where a and ![]() are two parameters to be determined later. So the Equation (15) is modified with the additional term in denominator as
are two parameters to be determined later. So the Equation (15) is modified with the additional term in denominator as
![]() (17)
(17)
In place of Equation (14) we now obtain the expression for ![]() as
as
![]() (18)
(18)
where the terms ![]() and
and ![]() represent the neutron and proton densities repectively and the integrals
represent the neutron and proton densities repectively and the integrals ![]() (with t = n for neutrons and p for protons) are given by
(with t = n for neutrons and p for protons) are given by
![]() (19)
(19)
where![]() . Finally we have to include the energy of repulsion which may arise from vector meson interaction and/or from finite size of the nuclei. We shall here parametrize the effect of such a repulsion contribution by the simple form
. Finally we have to include the energy of repulsion which may arise from vector meson interaction and/or from finite size of the nuclei. We shall here parametrize the effect of such a repulsion contribution by the simple form
![]() (20)
(20)
where the parameter ![]() corresponds to the repulsive ω-meson interaction between the nucleons fixed from phenomenology and can arise from local potential
corresponds to the repulsive ω-meson interaction between the nucleons fixed from phenomenology and can arise from local potential ![]() [18] [21] , when density is constant, in fact, we have
[18] [21] , when density is constant, in fact, we have
![]() (21)
(21)
Similarly, we have to include the repulsion energy from the ρ-mesons [20] [21]
![]() (22)
(22)
where ![]() and coefficient
and coefficient ![]() is to be evaluated self consistently as described below. We next minimise the energy per nucleon as given by
is to be evaluated self consistently as described below. We next minimise the energy per nucleon as given by
![]() (23)
(23)
where the total energy density ![]() is given from (8), (18), (20) and (22) as
is given from (8), (18), (20) and (22) as
![]() (24)
(24)
The total density ![]() and the asymmetric parameter t are given in terms of neutron density
and the asymmetric parameter t are given in terms of neutron density ![]() and proton density
and proton density ![]() as
as
![]() (25)
(25)
respectively. Now the expression for pressure is given by the equation
![]() (26)
(26)
The symmetry energy parameter ![]() in the expansion of the nuclear binding energy is given by [18] [20] [21]
in the expansion of the nuclear binding energy is given by [18] [20] [21]
![]() (27)
(27)
The symmetry energy slope is defined by
![]() (28)
(28)
The curvature parameter of symmetry energy slope is
![]() (29)
(29)
and the curvature parameter of the asymmetry energy is
![]() (30)
(30)
In the next section we study the stability condition considering the above properties of nuclear matter.
3. Stability Condition
Now the proton fraction is introduced to study the stability conditation as ![]() where t is asymmetry parameter (25). Here the free energy density is given by
where t is asymmetry parameter (25). Here the free energy density is given by
![]() (31)
(31)
where
![]() (32)
(32)
and
![]() (33)
(33)
In the above, ![]() and
and ![]() are chemical potential of proton and neutron respectively.
are chemical potential of proton and neutron respectively.
The stability conditation for asymmetric nuclear matter at constant temperature and constant volume are obtained from the free energy density ![]() imposing that it is a convex function of density
imposing that it is a convex function of density ![]() and
and ![]() [23] - [25] i.e. the symmetric stability matrix [19] [26]
[23] - [25] i.e. the symmetric stability matrix [19] [26]
![]() (34)
(34)
is positive-definite with i and j run for proton and neutron respectively. We note here that the equivalent condition for convex function [26]
![]() (35)
(35)
where we use
![]()
The two eigenvalues of the ![]() stability matrix are given by
stability matrix are given by
![]() (36)
(36)
and the eigenvectors ![]() by
by
![]() (37)
(37)
Both the eigenvalues of stability matrix as above should be positive to guarantee the stability of the system. Since the symmetry energy is dependent on the quadratic function of the asymmetry parameter (27) and a positive increasing symmetry energy with the total density (28), it ensure that only one eigenvalue can become negative. In principle ![]() will always be positive in isospin asymmetric nuclear matter.
will always be positive in isospin asymmetric nuclear matter. ![]() can only become negative and the eigenvector associated with this negative eigenvalue implies instability. Therefore, if Equation (36) is violated, or equivalently
can only become negative and the eigenvector associated with this negative eigenvalue implies instability. Therefore, if Equation (36) is violated, or equivalently ![]() is negative for isospin asymmetric nuclear matter, then the system will be in the unstable region of a phase transition [26] .
is negative for isospin asymmetric nuclear matter, then the system will be in the unstable region of a phase transition [26] .
4. Results and Discussions
The model presented here contains four parameters, namely the phenomenological strength and length scale parameters of meson repulsion a and ![]() (37) respectively and the strength parameters of the effective ω and ρ meson interactions namely,
(37) respectively and the strength parameters of the effective ω and ρ meson interactions namely, ![]() (20) and
(20) and ![]() (22) respectively. In our calculations, we evaluate all these parameters variationally. The first three of these four parameters are evaluated by constraining the binding energy per nucleon (23)
(22) respectively. In our calculations, we evaluate all these parameters variationally. The first three of these four parameters are evaluated by constraining the binding energy per nucleon (23) ![]() the pressure P and the compressibility K of the symmetric nuclear matter to the respective saturation values, i.e.
the pressure P and the compressibility K of the symmetric nuclear matter to the respective saturation values, i.e.![]() ,
, ![]() and
and ![]() [27] . The fourth parameter
[27] . The fourth parameter ![]() of our calculation is evaluated by fixing the value of
of our calculation is evaluated by fixing the value of ![]() to the standard value of 31 MeV [27] .
to the standard value of 31 MeV [27] .
We now discuss the results obtained in the calculations. Firstly the parameters are fixed using the saturation properties of the nuclear matter i.e. EB = −16 MeV and ρ0 = 0.15 fm−3 MeV. The pion-nucleon coupling constant is as ![]() and a = 115.264 MeV, Rπ = 1.061 fm, λω = 3.164 fm2 and λρ = 0.650 fm2. Then the discussion for results from the following figures shows the nature of variation and the effect of pion dressing of nuclear matter.
and a = 115.264 MeV, Rπ = 1.061 fm, λω = 3.164 fm2 and λρ = 0.650 fm2. Then the discussion for results from the following figures shows the nature of variation and the effect of pion dressing of nuclear matter.
In Figure 1, the symmetry energy variation is studied as the function of density. The variation of symmetry energy with density agrees with results of Non Linear Walecka Model (NL3) [28] , Quark Meson Coupling model (QMC) [29] and density-dependant relativistic Hadron model (TW) [30] , while our symmetry energy is relatively
![]()
Figure 1. The symmetry energy Esym as a function of nucleon density ρ.
less above density 0.2 fm−3. It is due to the effect of pion dressing as it is negative relative to ![]() and
and ![]() in the expression of total energy density
in the expression of total energy density ![]() in the higher densities.
in the higher densities.
In Figure 2, variation of the curvature parameter of the symmetry energy with density in the present study for both the compressibilities K = 270 and 290 coincides. Again our results agree almost with results of QMC [29] and agree nearly with that of NL3 [28] . It appears that the pion dressing of the nuclear matter in the present case hopefully gives better results.
The variation of slope of symmetry energy with density in Figure 3 shows that it starts decreasing in the very low densities i.e. up to ![]() and beyond this density the variation becomes relatively smooth and stabilizes at 90 MeV. It appears that the pion dressing of the nuclear matter improves over the results of TW and NL3.
and beyond this density the variation becomes relatively smooth and stabilizes at 90 MeV. It appears that the pion dressing of the nuclear matter improves over the results of TW and NL3.
In Figure 4, we show how the ratio of the proton and neutron density fluctuation changes with densities corresponding to the unstable mode. This also shows that the instability exits for the different proton fractions, although small, in the asymmetric nuclear matter (ANM). In Figure 4(a), for the proton fraction ![]() corresponding to the asymmetry parameter t = 0.9, it is observed that the variation of ratio of the proton and neutron density fluctuation with density does not agree at higher values but decreases rapidly and goes to zero at about 0.085 fm−3. In Figure 4(b), for the proton fraction
corresponding to the asymmetry parameter t = 0.9, it is observed that the variation of ratio of the proton and neutron density fluctuation with density does not agree at higher values but decreases rapidly and goes to zero at about 0.085 fm−3. In Figure 4(b), for the proton fraction ![]() which corresponds to the asymmetry parameter t = 0.8, the variation of ratio of proton and neutron density fluctuation with density agrees with results of TW [30] . In Figure 4(c), for the proton fraction
which corresponds to the asymmetry parameter t = 0.8, the variation of ratio of proton and neutron density fluctuation with density agrees with results of TW [30] . In Figure 4(c), for the proton fraction ![]() corresponding to the asymmetry parameter t = 0.4, the variation of ratio of the proton and neutron density fluctuation with density agrees and the saturation is relatively lower than that of TW [30] . In all the figures, it appears that the pion dressing of ANM has an effect which is much more pronounced and the ratio of density fluctuation of proton and neutron decreases with increase of total density. This trend is also observed in TW [30] .
corresponding to the asymmetry parameter t = 0.4, the variation of ratio of the proton and neutron density fluctuation with density agrees and the saturation is relatively lower than that of TW [30] . In all the figures, it appears that the pion dressing of ANM has an effect which is much more pronounced and the ratio of density fluctuation of proton and neutron decreases with increase of total density. This trend is also observed in TW [30] .
We show in Figure 5 that the variation of ratio of proton and neutron density fluctuation with proton fraction yp for a given density ρ = 0.06 fm−3 has an upward trend and reaches the value 1 at![]() . This also happens
. This also happens
![]()
Figure 2. The curvature parameter of symmetry energy ksym as a function of nucleon density ρ.
![]()
Figure 3. The slope parameter L as a function of nucleon density ρ.
![]()
Figure 4. The instability (eigenvector of negative eigenvalue) as a function of nucleon density ρ calculated for different values of the proton fraction yp = 0.05, 0.1 and 0.3.
![]()
Figure 5. The variation of negative eigenvector with the proton fraction yp for the value of ρ = 0.06 fm−3.
in all models ((NL3) [28] , (QMC) [29] and (TW) [30] ). Baring some differences, we note that the pion dressing of ANM is a need to understand to some extent its stability at zero temperature.